DS博客作业06--图
1.本周学习总结
1.思维导图
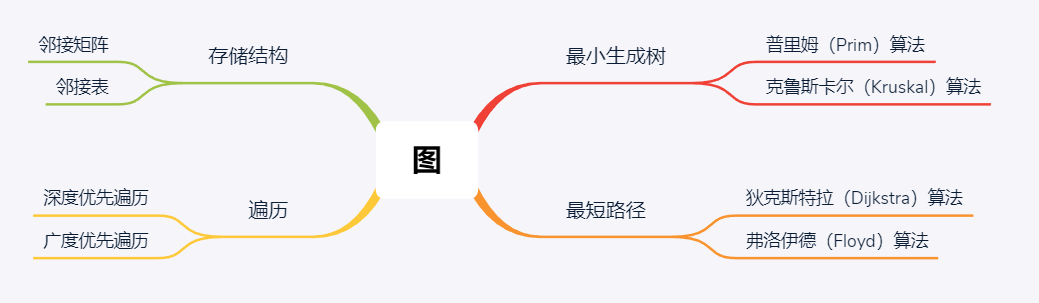
2.谈谈你对图结构的认识及学习体会。
其实在学习图之前我是有点担心学不好图的,因为之前学树的时候就已经花费了我很大的心力了,而图是一种比树更复杂的结构,但真正学起来的时候却发现图比树还要容易学一点,可能是图的各种操作递归用得比较少和存储结构更容易理解一点把。
2.PTA实验作业
2.1.题目1:7-3 六度空间
2.1.1设计思路
其实就是图的广度优先遍历
定义队列q
将起始节点入队并标记此节点已遍历过
while(队列不空)
{
p = G->adjlist[q.top()].firstarc;
q.pop();
n++;//记录遍历的节点数
while(p)
{
如果p未遍历则将其入队,并标记
p=p->nextarc;
}
if(当层的节点已遍历完)
{
h++;//遍历的层数+1
if(h>7)break;//遍历的层数超过7则结束遍历
}
}
return s;
2.1.2代码截图
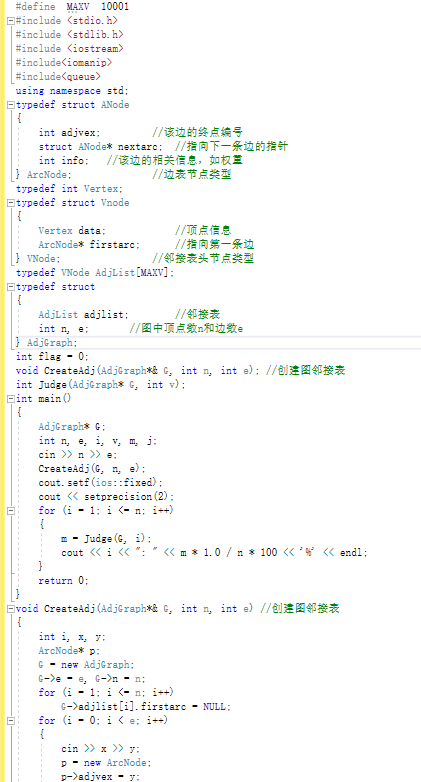
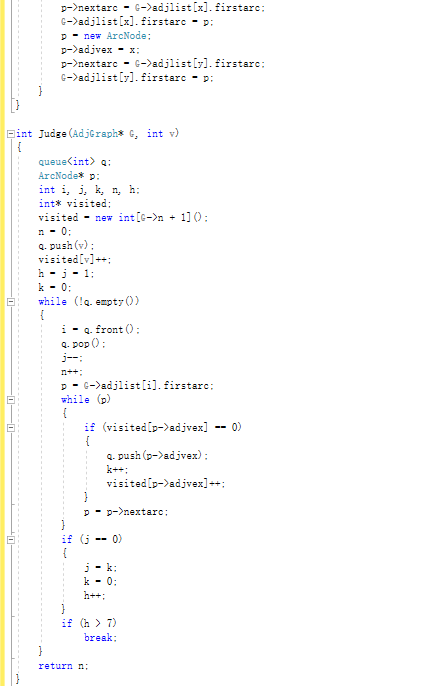
2.1.3本题PTA提交列表说明。
2.2 题目2:修建道路
2.2.1设计思路
其实就是建最小生成树,用克鲁斯卡尔算法做会简单一点
typedef struct
{
int u;//边的起始顶点
int v;//边的终止顶点
int w;//边的权值
}Edge;
定义Edge数组E[MAXV],整型数组vest[MAXV]
把边存入E中,并按升序排序
初始化数组vest
输入已存在的边并修改vest数组,每输入一次n就+1
while(n<g.n)
{
若边的起点与终点不属于同一个集合
s+=E.w;
合并两点所属的集合
n++
}
返回s
2.2.2代码截图
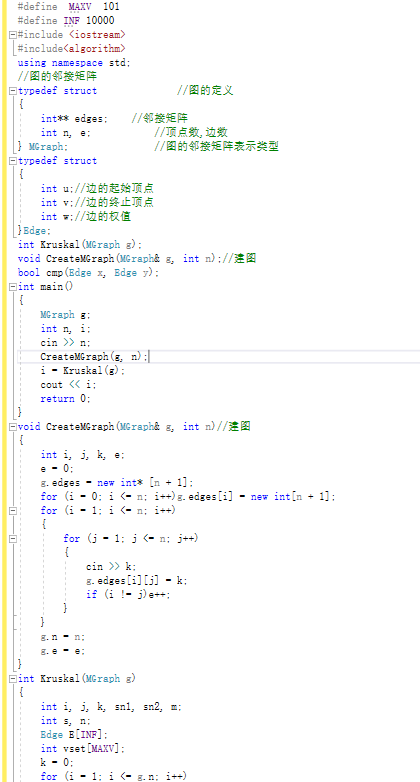
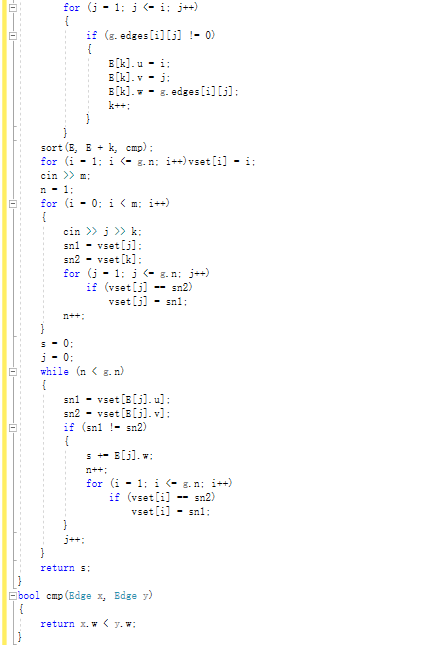
2.2.3本题PTA提交列表说明。

(其实这道题用并查集的,但我懒得改了,虽然并查集的代码也就十行左右。。。)
2.3 题目3:旅游规划
2.3.1设计思路
最短路径问题,可以用Dijkstra算法或Floyd算法解决,这里我用的是Floyd算法
初始化A和path数组
for(k=0;k<g.n;k++)
for(i=0;i<g.n;i++)
for(j=0;j<g.n;j++)
{
若从i到j的路径比从i到k再到j的路径短则修改A数组和path数组
若二者相同则记录两条路径中所花费的钱比较少的那条
}
2.3.2代码截图
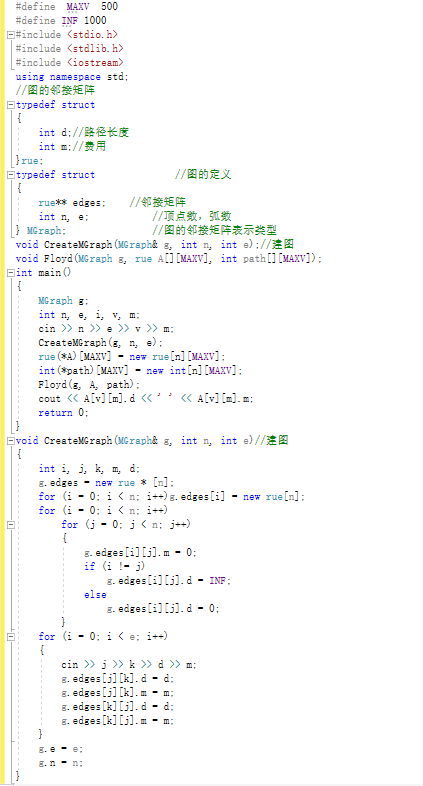

2.3.3本题PTA提交列表说明。

(其实这道题用Dijkstra算法来做更好,只不过Floyd算法代码比较少,所以我就用Floyd算法来做了。。。)
3.上机考试错题及处理办法
这次考试由于我对部分算法还不太熟练,解题所用的时间过长,导致最终没时间去解其余的题目
3.1.截图错题代码
考试时来不及做,交的代码是输出样例的,就不贴出来了。。。
3.2 错的原因及处理方法
6-1

(别问为什么没有7-3。。。)

