RANSAC 剔除错误匹配 估计模型

随机抽样一致，这个算法，我以前一直都没有理解透彻。只知道可以用来直线拟合，网上大多数中文博客也都是写直线拟合的，但是用来匹配二维特征的时候，总还是没弄明白。

基本概念参考 http://www.cnblogs.com/xrwang/archive/2011/03/09/ransac-1.html

写得已经够清楚了。

现在我来说说它在匹配特征时候的应用。

 

————————————————————————————————————————————

假如我有两组数据，M和T，其中T是由M经过一个旋转和一个平移得来的。

　　　　　　　　　　T=R*T+t

　　　　　　　　　　R=[cos(sita) -sin(sita); sin(sita) cos(sita)]

　　　　　　　　　　t=[tx;ty]

我现在已经大概知道了M的每组数与T的每组数据的对应关系 match,

　　　　　　　　　　match=[1 2; 3 4;5 6;……]

意思是：M的第1个  对应T的第2个；

　　　　M的第3个  对应T的第4个；

其中有一些对应错了。并且我不知道这个模型是啥。

我现在要做的，就是对这些东东进行ransac算法，找出这些错误的对应 outlier  ，找到其中正确的对应，并求出这个模型 R 、t

————————————————————————————————————————————

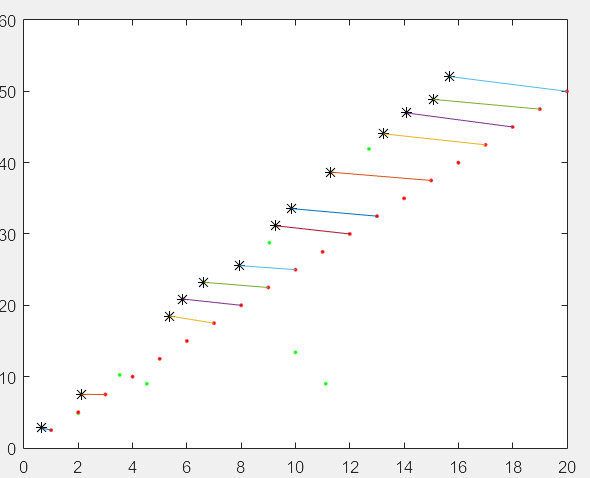
算法如下

1. 从match 里面，随机找出n组(n>=2,因为是三个未知数 sita tx ty,每组数可以列俩方程，所以四个方程已经够求三个未知数了)

2. 对这n组，求出R t， 具体方法可以使用svd法求刚体最小二乘转置 http://blog.csdn.net/kfqcome/article/details/9358853

3. 对这个求出来的R t,应用到T上，得到T'；结合match，找出T’中，不靠谱的（自己设一个阈值），就是outliers，靠谱的inliers

4. 对inliers的点，如2一样，求出新的R t

5. 评价这个模型，比如再进行一下3，求出inlier，inlier数目作为评价标准；或者inlier对M的误差作为标准。如果这个模型好 R_best=R   t_best=t

6.重复以上过程k次，最后的R_best  t_best就是结果了。

—————————————————————————————————————————————

就这样，可能哪里理解的不对，以后再改吧。目前来看，效果还是不错的。