洛谷P3408 恋爱

洛谷P3408 恋爱

树形DP

题目中有一个有一点歧义的地方，就是

“他的直属下属有不小于T分之Ai的人”

这里指的是所有他的下属总个数的T分之Ai

如果你还不理解，看样例

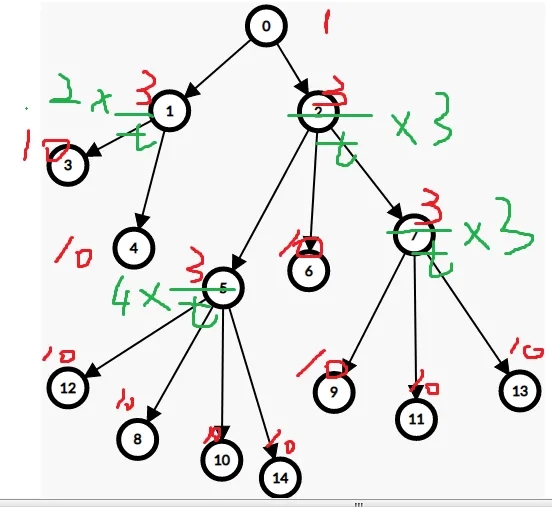
这下应该就明白了吧！

手动分割线

那么怎么写呢？

首先，每个叶子节点上书的代价就是A[i]没的说

那么其它节点呢？

对于其它任意一个节点X，当前节点上书的最小代价，就是有(SON[x] * A[i]/T)个代价最小的子节点上书的代价和

那就好整了，我们只需要用儿子节点里代价最小的那几个，来更新当前节点的代价就好了

code

#include <queue>
#include <iostream>
#include <cstring>
#include <cmath>
#define int long long//很方便
using namespace std;
 
const int N = 5e5 + 5;
 
int n,t,c;
 
int son[N];
int a[N];
int f[N];
 
int tot;
int head[N];
int to[N * 2];
int nxt[N * 2];
 
void add(int x,int y)
{
    to[++ tot] = y;
    nxt[tot] = head[x];
    head[x] = tot;
}
 
void dfs(int x)
{
    priority_queue <int,vector <int>,greater <int> > que;//小根堆
     //我用这个把儿子节点的代价排了序
    for(int i = head[x];i;i = nxt[i])
    {
        int y = to[i];
        dfs(y);
        que.push(f[y]);
    }
    f[x] = a[x];//子节点代价为a[x]
 
    if(que.size())
    {
        f[x] = 0;
        if(x)
        {
            for(int i = 1;i <= ceil(son[x] * a[x] * 1.0 / t);i ++)
            //ceil向上取整，得乘1.0，有点坑
            {
                int y = que.top();
                que.pop();
                f[x] += y;
            }
        }
        if(!x)//记得0和其它节点是不一样的
        {
            for(int i = 1;i <= ceil(son[x] * c * 1.0 / t);i ++)
            {
                int y = que.top();
                que.pop();
                f[x] += y;
            }
        }
    }
}
 
signed main()
{
    cin >> n >> t >> c;
    for(int i = 1;i <= n;i ++)
    {
        int x;
        cin >> x >> a[i];
        add(x,i);
        son[x] ++;
    }
    dfs(0);
    cout << f[0];
}