[luogu P2123] 皇后游戏 解题报告（贪心）

题目链接：https://www.luogu.org/problemnew/show/P2123

题目大意：

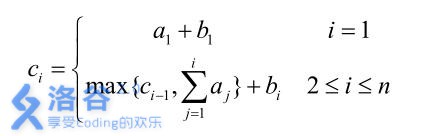
给定a数组和b数组，要求最小化c数组中的最大值

题解：

考虑微扰法，推一波式子先

设$x=\sum_{q=1}^{i-1}a[q]$，$y=c[i-1]$，与i相邻在i之后的大臣的编号为j

发现c数组是递增的，于是$max(c_i,c_j)=c_j$

$c_j=max(max(y,x+a_i)+b_i,x+a_i+a_j)+b_j$

$max(y+b_i+b_j,x+a_i+b_i+b_j,x+a_i+a_j+b_j)$

那么考虑交换i,j，同理交换后的较大值为

$max(y+b_i+b_j,x+a_j+b_i+b_j,x+a_j+a_i+b_i)$

我们假设交换之前是更优的，那么$max(y+b_i+b_j,x+a_i+b_i+b_j,x+a_i+a_j+b_j)<=max(y+b_i+b_j,x+a_j+b_i+b_j,x+a_j+a_i+b_i)$

发现有一部分是一样的那么上述结论成立的充分条件是

$max(x+a_i+b_i+b_j,x+a_i+a_j+b_j)<=max(x+a_j+b_i+b_j,x+a_j+a_i+b_i)$

化简一下得到

$max(b_i,a_j)-a_j-b_i<=max(b_j,a_i)-a_i-b_j$

$-min(b_i,a_j)<=-min(b_j,a_i)$

$min(b_i,a_j)>=min(b_j,a_i)$

 

 于是乎，我们考虑如何满足这个式子：

$a_i b_i$

$a_j b_j$

$a_k b_k$

相当于每个2*2正方形左对角最小值小于右对角的最小值

情况1：$b_j$最小

于是有$b_j<=a_j,b_j<=a_i$

又$b_j>=min(a_j,a_k)$

所以$b_k<=b_j<=a_j$

即b单调递减

情况2：$a_j$最小

于是有$a_j<=b_j,a_j<=b_k$

即a单调递增

又$a_j>=min(a_i,b_j)$

所以$b_j>=a_j>=a_i$

于是我们把情况2放在前面，情况1放在后面

情况2的前提是$b_j>=a_j$，情况1的前提是$b_j<=a_j$，正是因为包含等于号中间还有$b_j=a_j$的情况二者可以连接

设$d=\frac{a_i-b_i}{abs(a_i-b_i)}$

先按d值排序；然后若d值小于等于0，按a升序排序；若d值大于0，则按b降序排序

#include<algorithm>
#include<cstring>
#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;

const int N=2e4+15;
int n;
ll c[N];
struct node
{
    ll a,b;
    int d;
}p[N];
inline ll read()
{
    char ch=getchar();
    ll s=0,f=1;
    while (ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=getchar();}
    while (ch>='0'&&ch<='9') {s=(s<<3)+(s<<1)+ch-'0';ch=getchar();}
    return s*f;
}
bool cmp(node a,node b)
{
    if (a.d==b.d)
    {
        if(a.d==1) return a.b>b.b;
        else return a.a<b.a; 
    } 
    else return a.d<b.d;
}
int main()
{
    int T;
    T=read();
    while (T--)
    {
        n=read();
        for (int i=1;i<=n;i++)
        {
            p[i].a=read();p[i].b=read();
            if (p[i].a>=p[i].b) p[i].d=1;
            else p[i].d=-1; 
        }
        sort(p+1,p+1+n,cmp);
        ll s=0;
        for (int i=1;i<=n;i++)
        {
            s+=p[i].a;
            c[i]=max(c[i-1],s)+p[i].b;
        }
        printf("%lld\n",c[n]);
    }
    return 0;
}