[POJ2728] Desert King 解题报告(最优比率生成树)
题目描述:
David the Great has just become the king of a desert country. To win the respect of his people, he decided to build channels all over his country to bring water to every village. Villages which are connected to his capital village will be watered. As the dominate ruler and the symbol of wisdom in the country, he needs to build the channels in a most elegant way.
After days of study, he finally figured his plan out. He wanted the average cost of each mile of the channels to be minimized. In other words, the ratio of the overall cost of the channels to the total length must be minimized. He just needs to build the necessary channels to bring water to all the villages, which means there will be only one way to connect each village to the capital.
His engineers surveyed the country and recorded the position and altitude of each village. All the channels must go straight between two villages and be built horizontally. Since every two villages are at different altitudes, they concluded that each channel between two villages needed a vertical water lifter, which can lift water up or let water flow down. The length of the channel is the horizontal distance between the two villages. The cost of the channel is the height of the lifter. You should notice that each village is at a different altitude, and different channels can't share a lifter. Channels can intersect safely and no three villages are on the same line.
As King David's prime scientist and programmer, you are asked to find out the best solution to build the channels.
After days of study, he finally figured his plan out. He wanted the average cost of each mile of the channels to be minimized. In other words, the ratio of the overall cost of the channels to the total length must be minimized. He just needs to build the necessary channels to bring water to all the villages, which means there will be only one way to connect each village to the capital.
His engineers surveyed the country and recorded the position and altitude of each village. All the channels must go straight between two villages and be built horizontally. Since every two villages are at different altitudes, they concluded that each channel between two villages needed a vertical water lifter, which can lift water up or let water flow down. The length of the channel is the horizontal distance between the two villages. The cost of the channel is the height of the lifter. You should notice that each village is at a different altitude, and different channels can't share a lifter. Channels can intersect safely and no three villages are on the same line.
As King David's prime scientist and programmer, you are asked to find out the best solution to build the channels.
Input
There are several test cases. Each test case starts with a line containing a number N (2 <= N <= 1000), which is the number of villages. Each of the following N lines contains three integers, x, y and z (0 <= x, y < 10000, 0 <= z < 10000000). (x, y) is the position of the village and z is the altitude. The first village is the capital. A test case with N = 0 ends the input, and should not be processed.
Output
For each test case, output one line containing a decimal number, which is the minimum ratio of overall cost of the channels to the total length. This number should be rounded three digits after the decimal point.
Sample Input
4
0 0 0
0 1 1
1 1 2
1 0 3
0
Sample Output
1.000
题意:有一张无向图,每条边有费用值和长度值,要求找到一颗生成树,使得总费用/总长度最小
问题模型:最优比率生成树
解题方法:
设r=Σc[i]*x[i]/(Σl[i]*x[i])(x[i]=0/1)
目标,最小化r
变形得:Σc[i]*x[i]-r*Σl[i]*x[i]=0
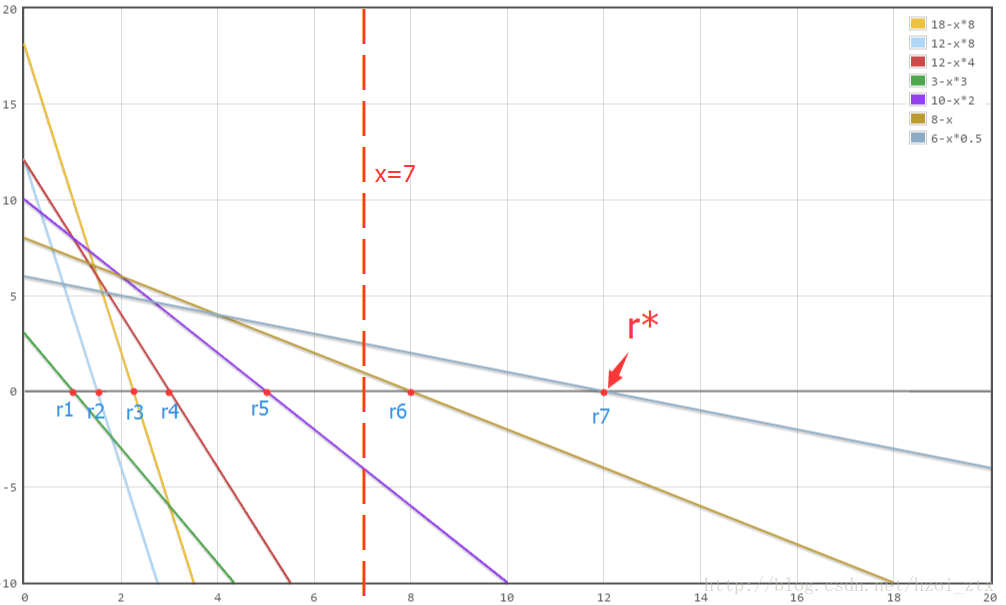
设f[r]=Σc[i]*x[i]-r*Σl[i]*x[i]于是对于每一组x[i],以我们得到一条直线,r是这条直线的横截距(确定x[i]之后其它的都是常数)我们的目标变成,找到全部直线中的最小横截距怎么找呢?首先暴力枚举x[i]绝对是不可取的。我们发现其实只需要二分r的值,然后观察min(f[r])就好,如果min(f[r])还要小于0的话,我们就可以知道r>r*(r*是我们最后的所求值),反之r<r*当我们我们发现min(f[r])==0时,我们认为r=r*然后就直接输出考虑一下二分的时间复杂度,完全没有问题(注意这里是最大化r,包括下面的图,最小化是同理的)
(图片来自大佬ztx的CSDN博客,https://blog.csdn.net/hzoi_ztx/article/details/54898323,感谢大佬)
然而,我们还有一种方法(DinkelbachDinkelbach算法)
基本思想,其实和二分有点像,但它是基于迭代的。我们考虑如上述二分,我们有一个初始值r,
然后我们发现min(f[r])还要小于0,
那我们就直接把r转移到min(f[r])所代表的直线的横截距上。读者细细想想
就知道,不可能得到一个比r*还要小的值,因为r*就是最小的截距了。
于是我们只需要不断迭代转移r就好了。
咳咳,差点忘了。怎么求min(f[r]),其实很显然,为了得到min(f[r])的x[i],
我们得把边的长度按照上面f函数的计算方法改一改跑最小生成树。
为什么呢?
首先这样我们肯定可以得到一组x[i]
同时最小就是保证了我们要算的f的取值最小
代码里是堆优化的prim(我懒。。。不手写堆的)
下面附上我的DinkelbachDinkelbach代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<memory.h>
#include<queue>
#include<math.h>
using namespace std;
const int maxn=1000+15;
int n,tot;
int head[maxn],in[maxn];
struct VILLAGE
{
double x;double y;double z;
}v[maxn];
struct EDGE
{
int from;int to;int next;double len;double cost;double e;
}edge[maxn<<12];
struct NODE{
int x;double l;double c;double d;
};
bool operator < (const NODE a,const NODE b){
return a.l>b.l;
}
void init(){
memset(edge,0,sizeof(edge));
memset(head,0,sizeof(head));
tot=0;
}
void add(int x,int y,double len,double cost){
edge[++tot]=(EDGE){x,y,head[x],len,cost,0};
head[x]=tot;
}
double prim(double oo)
{
memset(in,0,sizeof(in));
for (int i=1;i<=tot;i++)
{
edge[i].e=edge[i].cost-oo*edge[i].len;
//printf("%d %d %lf\n",edge[i].from,edge[i].to,edge[i].e);
}
priority_queue<NODE> q;
q.push((NODE){1,0,0,0});
int cnt=0;
double c1=0,d1=0;
while (!q.empty()&&cnt<n)
{
NODE k=q.top();q.pop();
if (in[k.x]) continue;
in[k.x]=1;
c1+=k.c;d1+=k.d;cnt++;
for (int i=head[k.x];i;i=edge[i].next)
{
int y=edge[i].to;
q.push((NODE){y,edge[i].e,edge[i].cost,edge[i].len});
}
}
//printf("\n%lf\n",c1/d1);
return c1/d1;
}
int main()
{
while (1)
{
scanf("%d",&n);
if (n==0) break;
init();
for (int i=1;i<=n;i++)
scanf("%lf%lf%lf",&v[i].x,&v[i].y,&v[i].z);
for (int i=1;i<n;i++)
for (int j=i+1;j<=n;j++)
{
double dis=sqrt((v[i].x-v[j].x)*(v[i].x-v[j].x)+(v[i].y-v[j].y)*(v[i].y-v[j].y));
double cost=fabs(v[i].z-v[j].z);
add(i,j,dis,cost);
add(j,i,dis,cost);
}
double r1=0.0,r2=0.0;
while (1){
r2=prim(r1);
if (fabs(r2-r1)<0.00001) break;
r1=r2;
}
printf("%.3f\n",r1);
}
return 0;
}
解决了最小的问题,最大的问题不也就迎刃而解了,只需要找最大截距就好了。这是0/1分数规划的典型之一。
其他的还有最优比率环什么的。
星星之火,终将成燎原之势


 浙公网安备 33010602011771号
浙公网安备 33010602011771号