【强化学习】DQN 算法改进

DQN 算法改进

（一）Dueling DQN

Dueling DQN 是一种基于 DQN 的改进算法。主要突破点：利用模型结构将值函数表示成更加细致的形式，这使得模型能够拥有更好的表现。下面给出公式，并定义一个新的变量：

\[q(s_t, a_t)=v(s_t)+A(s_t, a_t) \]

也就是说，基于状态和行动的值函数 \(q\) 可以分解成基于状态的值函数 \(v\) 和优势函数（Advantage Function）\(A\) 。由于存在：

\[E_{a_{t}}[q(s_t, a_t)] = v(s_t) \]

所以，如果所有状态行动的值函数不相同，一些状态行动的价值 \(q(s, a)\) 必然会高于状态的价值 \(v(s)\)，当然也会有一些低于价值。于是优势函数可以表现出当前行动和平均表现之间的区别：如果优于平均表现，则优势函数为正，反之为负。

以上是概念上的分解，以下是网络结构上对应的改变：

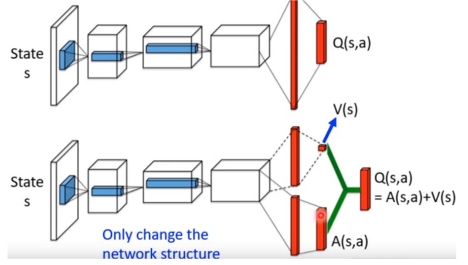
再保持主体网络不变的基础上，将原本网络中的单一输出变为两路输出，一个输出用于输出 \(v\) ，它是一个一维的标量；另一个输出用于输出 \(A\)，它的维度和行动数量相同。最后将两部分加起来，就是原来的 \(q\) 值。

如果只进行以上单纯地分解，会引出另外一个问题：当 \(q\) 值一定使，\(v\) 和 \(A\) 有无穷多种可行组合，我们可以对 \(A\) 函数做限定。我们知道 \(A\) 函数地期望为 0：

\[E_a[A(s_t, a_t)] = E_{a}[q(s_t, a_t)-v(s_t)]=v(s_t)-v(s_t)=0 \]

对 \(A\) 值进行约束，将公式变为：

\[q(s_t, a_t) =v(s_t)+(A(s_t, a_t)- \frac{1}{|A|}\sum_{a'}A(s_t, a_t^{'})) \]

让每一个 \(A\) 值减去当前状态下所有 \(A\) 值得平均数，就可以保证前面提到的期望值为 0 的约束，从而增加了 \(v\) 和 \(A\) 的输出稳定性。

实际意义： 将值函数分解后，每一部分的结果都具有实际意义。通过反卷积操作得到两个函数值对原始图像输入的梯度后，可以发现 \(v\) 函数对游戏中的所有关键信息都十分敏感，而 \(A\) 函数只对和行动相关的信息敏感。

（二）Priority Replay Buffer

Priority Replay Buffer 是一种针对 Replay Buffer 的改进结构。Replay Buffer 能够提高样本利用率的同时减少样本的相关性。它存在一个问题：每个样本都会以相同的频率被学习。但实际上，每个样本的难度是不同的，学习样本所得的收获也是不同的。为了使学习的潜力被充分挖掘出来，就有研究人员提出了 Priority Replay Buffer。它根据模型对当前样本的表现情况，给样本一定的权重，在采样时被采样的概率就和这个权重有关。交互时表现越差，对应权重越高，采样的概率也就越高。反之，如果表现越好，则权重也就降低，被采样的概率也就降低。这使得模型表现不好的样本可以有更高的概率被重新学习，模型会把更多精力放在这些样本上。

从算法原理来看，Priority Replay Buffer 与以往的 Replay Buffer 有两个差别：

（1）为每一个存入 Replay Buffer 的样本设定一个权重；

（2）使用这个权重完成采样过程：由于采样的复杂度较高，我们可以采用线段树数据结构来实现这个功能。

---

References

​ [1] 《强化学习精要——核心算法与 Tensorflow 实现》冯超