1761. 一个图中连通三元组的最小度数

给你一个无向图，整数 n 表示图中节点的数目，edges 数组表示图中的边，其中 edges[i] = [ui, vi] ，表示 ui 和 vi 之间有一条无向边。

一个 连通三元组 指的是 三个 节点组成的集合且这三个点之间 两两 有边。

连通三元组的度数 是所有满足此条件的边的数目：一个顶点在这个三元组内，而另一个顶点不在这个三元组内。

请你返回所有连通三元组中度数的 最小值 ，如果图中没有连通三元组，那么返回 -1 。

 

示例 1：

 

 

 

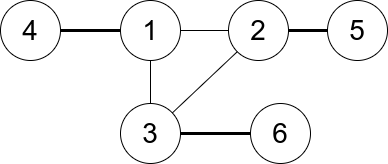
输入：n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
输出：3
解释：只有一个三元组 [1,2,3] 。构成度数的边在上图中已被加粗。

示例 2：

 

 

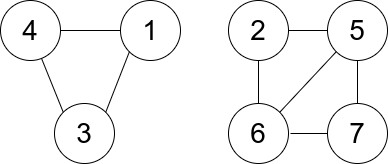
输入：n= 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]

输出：0
解释：有 3 个三元组：
1) [1,4,3]，度数为 0 。
2) [2,5,6]，度数为 2 。
3) [5,6,7]，度数为 2 。

 

提示：

• 2 <= n <= 400
• edges[i].length == 2
• 1 <= edges.length <= n * (n-1) / 2
• 1 <= ui, vi <= n
• ui != vi
• 图中没有重复的边。

 

 

class Solution {
    bool e[401][401];
    int degree[401];
public:
    int minTrioDegree(int n, vector<vector<int>>& edges) {
        bool have=false;
        int res=INT_MAX;

        for(auto &i:edges){
            e[i[0]][i[1]]=true;
            e[i[1]][i[0]]=true;
            degree[i[0]]++;
            degree[i[1]]++;
        }
        
        //To get the trios (u,v,w)
        for(int i=1;i<=n;i++){//iterate on each w,v
            for(int j=i+1;j<=n;j++){//w and v are neighbors of each other.
                if(!e[i][j])continue;
                    for(int k=1;k<=n;k++){//iterate on u
                        if(!e[i][k]||!e[j][k])continue;//w and v are neighbors of u
                        have=true;
                        res=min(res,degree[i]+degree[j]+degree[k]-6);
                        //The degree of the trio is just degree(u) + degree(v) + degree(w) - 6. The -6 comes from subtracting the edges u-v, u-w, and v-w, which are counted twice each in the vertex degree calculation.
                    }
            }
        }

        if(!have)return -1;
        return res;
    }
};