32. 最长有效括号

给定一个只包含 '(' 和 ')' 的字符串，找出最长的包含有效括号的子串的长度。

示例 1:

输入: "(()"
输出: 2
解释: 最长有效括号子串为 "()"
示例 2:

输入: ")()())"
输出: 4
解释: 最长有效括号子串为 "()()"

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-valid-parentheses

栈

典型的栈结构

栈中初始化一个 -1，作为分割符；

遇到'('入栈，遇到')'出栈；

当栈为空时且当前扫到的是')'，把它入栈作为分割符；

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        if not s:
            return 0
        res=0
        stack=[-1]
        for i in range(len(s)):
            if s[i]=='(':
                stack.append(i)
            else:
                stack.pop()
                if not stack:
                    stack.append(i)
                else:
                    res=max(res,i-stack[-1])
        return res

• time：O(N)
• space：O(N)

 

暴力=>优化

 

先写出暴力

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        n = len(s)
        res = 0

        def Cnt(start):
            cnt = 0
            res = 0
            for i in range(start, n):
                if s[i] == '(':
                    cnt += 1
                if s[i] == ')':
                    cnt -= 1
                if cnt < 0:
                    return i - start
                if cnt == 0:
                    res = max(res, i - start + 1)
            return res
        for i in range(n):
            res = max(res, Cnt(i))

        return res

同样是计数，我们会想到用两个指针l,r分别记录左右括号的数量 ；如果 r > l ，说明上次可以匹配的括号到当前的括号这一段不能匹配，重置 l 和 r 为 0；如果 r== l, 此时可以匹配，更新res

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        l=r=res=0
        for i in s:
            if i=='(':
                l+=1
            else:
                r+=1
            if l==r:
                res=max(res,l+r)
            if r>l:
                l=r=0

        #针对((((()这种情况逆序遍历一遍
        l=r=0
        for i in s[::-1]:
            if i=='(':
                l+=1
            else:
                r+=1
            if l==r:
                res=max(res,l+r)
            if r<l:
                l=r=0 

        return res

dp

 

 

 

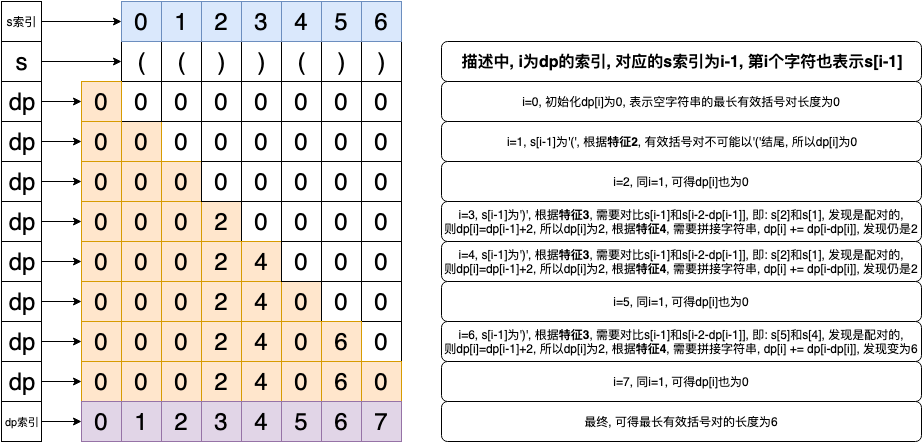
 （图片来自网络）

py

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        res = 0
        dp = [0] * (len(s) + 1)
        for i in range(1, len(s) + 1):
            if s[i - 1] == '(':
                continue
            left = i - 2 - dp[i - 1]
            if left >= 0 and s[left] == '(':
                dp[i] = dp[i - 1] + 2
                if dp[i - dp[i]]:
                    dp[i] += dp[i - dp[i]]  
                res =max(res,dp[i])

        return res

 c++

class Solution {
public:
    int longestValidParentheses(string s) {
        int res=0;
        int n=s.size();
        vector<int>dp(n+1);
        for(auto i:dp)i=0;
        for(int i=1;i<=n;i++){
            if(s[i-1]=='(')continue;
            int left=i-2-dp[i-1];
            if(left>=0&&s[left]=='('){
                dp[i]=dp[i-1]+2;
                if(dp[i-dp[i]]){
                    dp[i]+=dp[i-dp[i]];
                }
                res=max(res,dp[i]);
            }
        }
        return res;
    }
};