leetcode84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

 

 

 

 

 

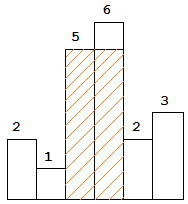
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

当前的数字向两边拓展，遇到比自己大的就接着拓展，小的就停止，然后用自己的高度乘以拓展的宽度，每次都跟新最大面积，时间复杂度为O(N^2),tle

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        l, r, ans = [-1] * n, [n] * n, 0
        for i in range(1, n):
            j = i - 1
            while j >= 0 and heights[j] >= heights[i]:
                j -= 1
            l[i] = j
        for i in range(n - 2, -1, -1):
            j = i + 1
            while j < n and heights[j] >= heights[i]:
                j += 1
            r[i] = j
        for i in range(n):
            ans = max(ans, heights[i] * (r[i] - l[i] - 1))
        return ans

实际上我们内层循环没必要一步一步移动，我们可以直接将j -= 1 改成 j = l[j], j += 1 改成 j = r[j]

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n=len(heights)
        l,r,ans=[-1]*n,[n]*n,0
        for i in range(1,n):
            j=i-1
            while j>=0 and heights[j]>=heights[i]:
                j=l[j]
            l[i]=j
        for i in range(n-2,-1,-1):
            j=i+1
            while j<n and heights[j]>=heights[i]:
                j=r[j]
            r[i]=j
        for i in range(n):
            ans=max(ans,heights[i]*(r[i]-l[i]-1))
        return ans

AC

如果熟悉单调栈的话，很容易想到

单调栈法：

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n,heights,st,ans=len(heights),[0]+heights+[0],[],0
        for i in range(n+2):
            while st and heights[st[-1]]>heights[i]:
                ans=max(ans,heights[st.pop(-1)]*(i-st[-1]-1))
            st.append(i)
        return ans