素数判定与筛法

素数判定相关。包括筛法,也含更基础的算法及其常数优化。Pollard-Rho一类的就别想了。不会。
本文是我第一次使用 \(\LaTeX\) ,以\(Markdown\)编辑。
一、朴素算法
根据定义,枚举判断正整数 \(n\) 是否有除\(1\)和它本身以外的因数即可。时间复杂度 \(O(n)\) 。大数据下时间过长是显然的。
bool is_prime(int n){
if(n == 1) return false;
if(n == 2) return true;
for(int i=2; i<n; i++)
if(n % i == 0) return false;
return true;
}
二、一个小但有用的优化
由于\(n\)的因数为成对出现的,我们只枚举了其中一个,枚举范围到\(\sqrt{n}\)即可。
bool is_prime(int n){
if(n == 1) return false;
if(n == 2) return true;
for(int i=2; i*i<=n; i++)
if(n % i == 0) return false;
return true;
}
其实,这种优化后时间复杂度为\(O(\sqrt{n})\),已经可以满足大多数使用场合了。
三、又一个常数优化
这里要利用到一个定理:所有大于\(3\)的质数取余\(6\),得数均为\(1\)或\(5\)。即,所有大于\(3\)的质数均为\(6k+1\)或\(6k-1\)。
反证法证明如下:
取余结果只可能为\(0\) ~ \(5\)。若为\(0\)、\(2\)或\(4\),则为偶数,不可能为质数。若为\(3\),则可以被\(3\)整除,不可能为质数。
因此,对于取余结果不为\(1\)或\(5\)的数,可以\(O(1)\)得出该数不为质数。否则枚举\(6k\pm1\)即可。
bool is_prime(int n)
{
if(n == 1) return false;
if(n == 2 || n == 3) return true;
if(n % 6 != 1 && n % 6 != 5) return false;
for(int i=5; i*i<=n; i+=6)
if(n % i == 0 || n % (i + 2) == 0) return false;
return true;
}
理论上最坏效率是上一个小优化后的三倍,即,时间复杂度\(O(\sqrt{n} / 3)\)。
四、本文主要内容:筛法
筛法用于预处理出一定区间内的质数,便于使用时\(O(1)\)查询。主要的我现在会的方法有一般筛法(埃拉托斯特尼筛法)与欧拉筛。
埃拉托斯特尼筛法:先将所有数标为质数,每次选取最前面的质数,将其所有倍数标为合数。
gif演示见下(来自维基百科):
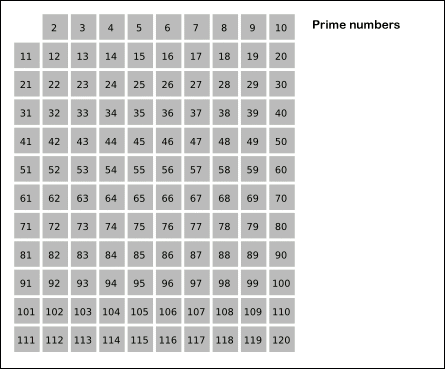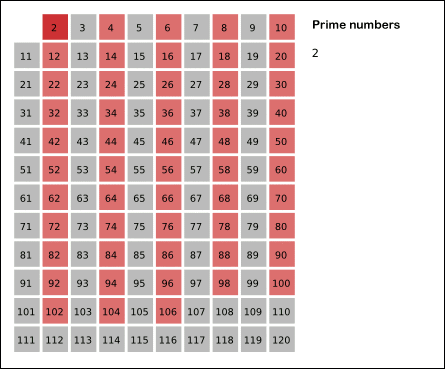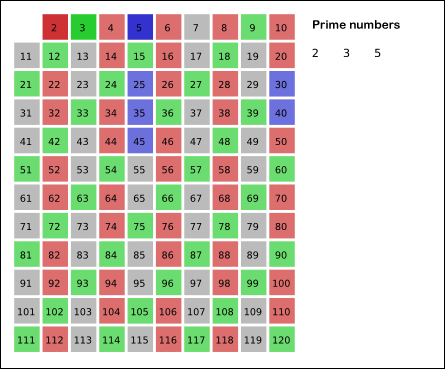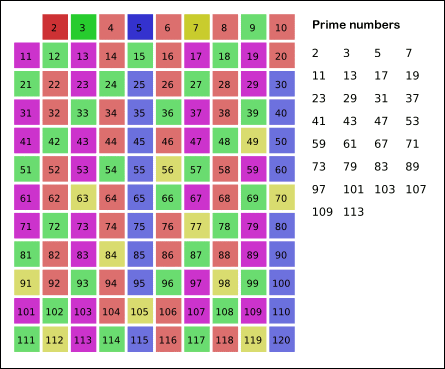
但是,由于有的数会被重复计算(如\(6\)被\(2\)和\(3\)均标记一次),达不到线性。
时间复杂度\(O(n\ log\ log\ n)\)。(我并不会算)
bool prime[MAXN];
void make_prime() {
memset(prime, true, sizeof(prime));
prime[0] = prime[1] = false;
int sq = sqrt(MAXN);
for(int i=2; i<=t; i++) {
if(prime[i]) {
for(int j=2*i; j<MAXN; j+=i) {
prime[j]=false;
}
}
}
}
由于以上弊端,经过改良后的筛法——欧拉筛,可以达到保证每个合数只在最小质因子时被筛出。
bool prime[MAXN];
int Prime[MAXN];
int num=0;
void make_prime(){
memset(prime, true, sizeof(prime));
prime[0] = prime[1] = false;
for(int i=2; i<=MAXN; i++) {
if(prime[i]) {
Prime[num++]=i;
}
for(int j=0; j<num && i*Prime[j]<MAXN; j++) {
prime[i * Prime[j]]=false;
if(!(i % Prime[j]))
break;
}
}
}
该筛法的时间复杂度可以达到\(O(n)\),基本满足各种需求。
注意,筛法不能用于数较大但请求较少的情况,否则会付出较大的时间和空间。
五、就这么一提其他算法
\(Miller–Rabin\ primality\ test\):更高效,虽然是一种不确定的质数判断法,但是在选择多种底数的情况下,正确率是可以接受的。
\(Pollard\ Rho\)是一个非常玄学的方式,用于在\(O(n^{1/4})\)的期望时间复杂度内计算合数n的某个非平凡因子。事实上算法导论给出的是\(O(\sqrt p)\),\(p\)是\(n\)的某个最小因子,满足\(p\)与\(n/p\)互质。但是这些都是期望,未必符合实际。但事实上\(Pollard~Rho\)算法在实际环境中运行的相当不错。
\(the\ Meissel,Lehmer,Lagarias,Miller,Odlyzko\ Method\):我也不知道它是啥,传说中的\(O(n^{3/4}/log\ n)\)


