Python排序算法（五）——希尔排序(Shell’s Sort)

 

有趣的事，Python永远不会

如需转发，请注明出处：小婷儿的python  https://www.cnblogs.com/xxtalhr/p/10793487.html 

一、希尔排序(Shell’s Sort)

　　希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本，它与插入排序的不同之处在于，它会优先比较距离较远的元素，该方法因D.L.Shell于1959年提出而得名。

　　希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。希尔排序是基于插入排序的以下两点性质而提出改进方法的：

　　插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率；

　　但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位；

　　希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序。

1、原理

　　　　希尔排序的整体思想是将固定间隔的几个元素之间排序，然后再缩小这个间隔。这样到最后数列就成为了基本有序数列，而前面我们讲过插入排序对基本有序数列排序效果较好。

1. 计算一个增量（间隔）值

2. 对元素进行增量元素进行比较，比如增量值为7，那么就对0,7,14,21…个元素进行插入排序

3. 然后对1,8,15…进行排序，依次递增进行排序

4. 所有元素排序完后，缩小增量比如为3，然后又重复上述第2，3步

5. 最后缩小增量至1时，数列已经基本有序，最后一遍普通插入即可

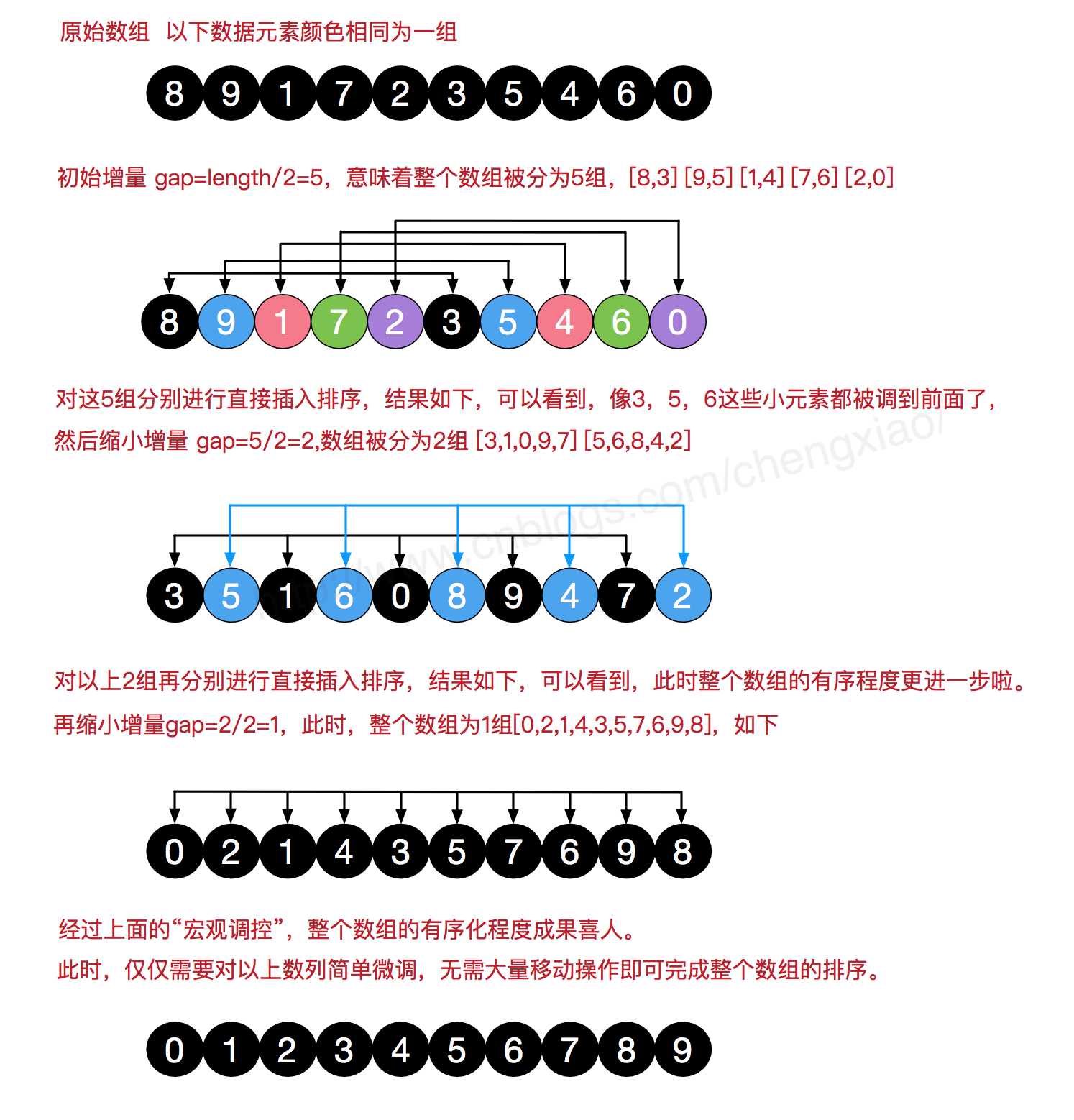　　　　　　　　　　　　　　　　　　　　　　　图片来源：https://www.cnblogs.com/chengxiao/p/6104371.html

　　2、希尔排序详解

• 希尔排序在排序前：将一个序列分成了好几个序列
• 在第一趟排序时：将这几个序列做插入排序。排序后，部分较大的数字往后靠，部分较小的数字往前靠
• 在第二趟排序时：将这个序列又分了好几个序列做插入排序(但比第一次分的数要少,ps:如果第一次分5个，第二次可能就2个了)。排序后，部分较大的数字往后靠，部分较小的数字往前靠
• ................
• 在第n趟排序时：将这个序列又分了好几个序列(直到剩下一个序列)，从宏观上看，此序列就基本是有序的了。这时就用简单插入排序将数列直至已序

　　从直观上看希尔排序：就是把数列进行分组(不停使用插入排序)，直至从宏观上看起来有序，最后插入排序起来就容易了(无须多次移位或交换)。

　　3、举例　　　

　举个例子，假设我现在有一个数列  

　　　　[11, 99, 33 , 69, 77, 88, 55, 11, 33, 36,39, 66, 44, 22] ，使用希尔排序的详细步骤：

• 首先，gap = length / 2=7，数组分为7组

　　　　 [11, 11],[ 99 , 33], [33, 36], [69, 39],[ 77, 66],[88, 44], [55, 22] 

• 然后，对7组分别插入排序，像33,39,66,44,22这些元素被调到前面，

　　　　1 [11, 11],[ 33 , 99], [33, 36], [39, 69],[ 66, 77],[44, 88], [22, 55] 

• 接着，数组变为 

　　　　[11, 11,33 , 99, 33, 36, 39, 69, 66, 77,44, 88, 22, 55]

　　　　gap = length / 2=3，数组分为3组，

　　　　 [11,99,39,77,22],[11,33,69,44,55],[33,36,66,88]

• 以此类推，gap = length / 2=1列表变为 

　　　　 1 [11,22,39,77,99,11,33,44,55,69,33,36,66,88]

• 最终对数组微调，得到列表 

　　　　 1 [11, 11, 22, 33, 33, 36, 39, 44, 55, 66, 69, 77, 88, 99] 

 

 二、代码

 　　代码用jupyternotebook实现

 　　在希尔排序的理解时，我们倾向于对于每一个分组，逐组进行处理，但在代码实现中，我们可以不用这么按部就班地处理完一组再调转回来处理下一组（这样还得加个for循环去处理分组）比如[5,4,3,2,1,0] ，首次增量设gap=length/2=3,则为3组[5,2] [4,1] [3,0]，实现时不用循环按组处理，我们可以从第gap个元素开始，逐个跨组处理。同时，在插入数据时，可以采用元素交换法寻找最终位置，也可以采用数组元素移动法寻觅。希尔排序的代码比较简单，如下：

def shell_sort(arr):
    """希尔排序"""
    # 取整计算增量（间隔）值
    gap = len(arr) // 2
    while gap > 0:
        # 从增量值开始遍历比较
        for i in range(gap, len(arr)):
            j = i
            current = arr[i]
            # 元素与他同列的前面的每个元素比较，如果比前面的小则互换
            while j - gap >= 0 and current < arr[j - gap]:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = current
        # 缩小增量（间隔）值
        gap //= 2
    return arr

shell_sort([11, 11, 22, 33, 33, 36, 39, 44, 55, 66, 69, 77, 88, 99])

# 返回结果[11, 11, 22, 33, 33, 36, 39, 44, 55, 66, 69, 77, 88, 99]

 

三、特点　

• 比较性：排序时元素之间需要比较，所以为比较排序

• 稳定性：因为希尔排序是间隔的插入，所以存在相同元素相对顺序被打乱，所以是不稳定排序

• 时间复杂度：    最坏时间复杂度O(n^2)平均复杂度为O(n^1.3)

• 空间复杂度：只需要常数个辅助单元，所以空间复杂度也为O(1)

• 记忆方法：插入排序是每轮都是一小步，希尔排序是先大步后小步，它第一个突破O(n2)的排序算法。联想起阿姆斯特朗登月之后说：这是我个人一小步，却是人类迈出的一大步。

结果　　　

　　Successfully ！！！

　　有趣的事，Python永远不会缺席！还不来加我，瞅什么瞅。