关于SVM数学细节逻辑的个人理解(一) :得到最大间隔分类器的基本形式
网上,书上有很多的关于SVM的资料,但是我觉得一些细节的地方并没有讲的太清楚,下面是我对SVM的整个数学原理的推导过程,其中逻辑的推导力求每一步都是有理有据。现在整理出来和大家讨论分享。
因为目前我的SVM的数学原理还没有过多的学习核函数,所以下面的整理都不涉及到核函数。而且因为很多地方我还没理解太透,所以目前我整理的部分主要分为:
①最大间隔分类器,其中包括优化目标的一步步推导,还有关于拉格朗日函数,KKT条件,以及对偶问题等数学优化的知识
②软间隔优化形式,即加入了松弛变量的优化目标的一步步推导
③SMO算法
下面是第一部分,得到SVM的基本形式。
一.前言:
虽然还是有很多地方不能理解,但是我觉得目前理解的程度已经进入了一个瓶颈了,或许从头整理一遍会突破呢。(后来证明确实自己整理推导一遍有很大的收获)
不得不说SVM是真的难,神经网络如果说难就难在反向传播算法,不过那也只是个链式求导法则,而SVM则涉及到最优化的大量数学知识,毕竟光是一个SVM就能写本书(《支持向量机导论》)的...
OK,开始整理整个SVM的思路。可能一开始还是有很多不清楚的地方,不过慢慢修改吧。
而且想要自己画一些图,但是目前还没找到好的工具,所以就先剪切一些书上的图,我会标注好来源的。
二.得到最最基本的形式
(不知道起什么题目更好)

(图来自于《机器学习》P121)
我觉得很多人可能对SVM要做什么很熟悉了,现在还是啰嗦一下:
现在给你训练数据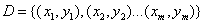 ,其中
,其中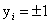 (牢记这个,在后面很重要),我们要做的就是找到一个超平面可以把这两类数据给分开。现在假设,这个数据集是线性可分的(先考虑数据集是线性可分的情况),那么我们其实可以找到很多超平面来分开这两类数据,比如上面这个图中可以看到由很多情况。那么我们该找哪种情况呢?
(牢记这个,在后面很重要),我们要做的就是找到一个超平面可以把这两类数据给分开。现在假设,这个数据集是线性可分的(先考虑数据集是线性可分的情况),那么我们其实可以找到很多超平面来分开这两类数据,比如上面这个图中可以看到由很多情况。那么我们该找哪种情况呢?
直观上看,我们需要找的这个超平面,它离两边的不同类型的数据集距离“最远”,就比如上面加粗的那条直线。这个直线看起来距离两类数据集是“最远的”,这样在预测时可能更准确一些,这个我觉得大家都能理解。但这是直观上的说法,如果要使用数学原理来解决,我们首先需要找到衡量平面到数据集的距离远近的标准,这就引出了“函数间隔”和“几何间隔”的概念。
(寻找最大间隔直观上看是最优的,而且其实背后有对应的数学原理,我记得在《支持向量机导论》中应该是第四章讲了,但是目前还是没太理解,大家有兴趣可以看一看)
1.函数间隔与几何间隔定义
首先我们定义超平面的表达式为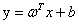 ,那么复习一下高中学的知识我们知道,平面上一个点x到这个平面的距离是
,那么复习一下高中学的知识我们知道,平面上一个点x到这个平面的距离是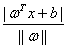 ,而这个就是几何间隔的定义。
,而这个就是几何间隔的定义。
(如果不熟悉这个,那肯定熟悉一个点(x,y)到Ax+By+C=0,的距离公式是 )
)
而函数间隔是什么呢?这里就需要强调的取值了: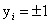 ,对于正样例它的label是+1,对于负样例它的label是-1。(所以乘上不改变原来的绝对值)
,对于正样例它的label是+1,对于负样例它的label是-1。(所以乘上不改变原来的绝对值)
我们用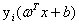 来表示一个样本点
来表示一个样本点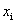 到这个超平面的函数间隔。
到这个超平面的函数间隔。
(关于函数间隔的定义是在《支持向量机导论》第二章中找到的)
2.函数间隔与几何间隔的关系
需要注意的是,如果找到了一个超平面可以正确分开这个数据集,那么意味着对于每个样本点x来说,其实它的函数间隔都大于等于0,即:

我觉得这一步理解很关键。具体解释就是:对于正样例,因为它的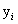 =1,而因为它被正确分类了,所以它的
=1,而因为它被正确分类了,所以它的 ,所以可以得到
,所以可以得到 ,对于负样例同理。
,对于负样例同理。
(很多书上直接给出 ,我觉得思维跨度就有点大了,关于
,我觉得思维跨度就有点大了,关于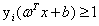 的说明后面讲)
的说明后面讲)
然后进一步我们其实可以得到,如果这个样本被正确分类了,那么:

所以函数间隔其实也可以用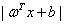 表示。
表示。
回顾之前几何间隔的计算式子 ,很多时候其实分子都不用绝对值符号来表示,我们可以把分子的绝对值换成函数间隔,那么这个样本到超平面的几何间隔其实就可以写成:
,很多时候其实分子都不用绝对值符号来表示,我们可以把分子的绝对值换成函数间隔,那么这个样本到超平面的几何间隔其实就可以写成:
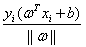
所以我觉得这就是函数间隔和几何间隔之间的关系,即在样本集线性可分的情况下,对于某一个成功分类的超平面来说,每个样本点到这个超平面的几何间隔就是函数间隔再除以的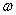 范数。
范数。
3.定义超平面到训练集的间隔
然后我们之前的几何间隔,函数间隔什么的都是点到平面的距离,现在我们定义一个超平面到训练集的间隔为这个超平面到训练集的每个点的几何距离中最小的距离。
(关于这个的定义我是参考了《Pattern Recognition and Machine Learning 》关于SVM的讲解,这本书是我见过的讲的最细的了)
这个平面到数据集的间隔就是我们一开始直观感受时所需要的那个衡量远近的数值。
从这个意义上来说,其实我们在衡量一个平面到数据集的“远近”时,我们其实只需要看的是到所有的样本点距离中最近的那个。
所以对于一个超平面(ω,b)我们可以得到它到给定训练集的间隔为:
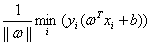
这个式子很容易理解,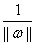 如果放进min里面,即
如果放进min里面,即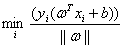 ,就表示在每个几何间隔中找最小的。因为
,就表示在每个几何间隔中找最小的。因为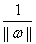 和具体样本点无关所以被提了出来,然后后面的
和具体样本点无关所以被提了出来,然后后面的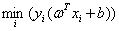
就是表示训练集中每个点到这个超平面的函数间隔中的最小值。
这里还需要理解的是,如果给定了这个分类超平面,那么这个超平面到训练集的距离就定了,因为训练集是给定了每个点是固定的。所以超平面如果调整,这个间隔就会变化。
4.得到最最原始的优化目标
所以我们现在需要找到这么一个超平面,它不但可以正确分类,而且它到训练集的间隔是所有可正确分类的超平面中最大的。这也是我们一开始提出的那个直观上的问题。
然后我们就可以得到我们的最最原始的优化目标了:

(写到这里我在想一个问题,如何能保证按照这个优化目标找出来的超平面它正好到正样本集和负样本集的间隔是一样的。经过思考后发现,这个已经被包含在了这个优化目标内部。可以这么解释:因为其实我觉得我们可以把平面优化分为ω的最优化和b的最优化,对于相同的ω,不同的b的平面都是平行的。当ω固定时,这时一个正样本到这个平面的距离和一个负样本到这个平面的距离之和的最小值也固定了!后面补图说明。
但是不同的b会导致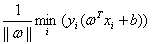 不同,不同的b会导致平面保持相同的“斜率”平移。发现因为这里取最小值。所以我们假设这个平面从正负样本的正中间往正样本方向偏离一小段距离,那么可能是到正样本距离变小,到负样本的距离变大,但是注意到
不同,不同的b会导致平面保持相同的“斜率”平移。发现因为这里取最小值。所以我们假设这个平面从正负样本的正中间往正样本方向偏离一小段距离,那么可能是到正样本距离变小,到负样本的距离变大,但是注意到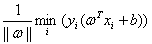 是取最小值,所以这个最小值就会从原来的1/2变小,并不是我们最后的最优的结果,所以从这个角度看,直线位于正中间是最优的。)
是取最小值,所以这个最小值就会从原来的1/2变小,并不是我们最后的最优的结果,所以从这个角度看,直线位于正中间是最优的。)
(这个最原始的优化目标很多书上都没有,我也是在《Pattern Recognition and Machine Learning》这本书上找到的,这本书相当不错)
三.得到SVM的基本形式
得到这个最最原始的优化目标后,直接尝试解决它是很复杂的。我们还可以进一步简化。注意到如果我们对ω和b同时进行缩放,即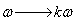 ,
, ,然后把kω和kb代入原来的式子
,然后把kω和kb代入原来的式子 ,会发现对原来的优化问题并没有影响,因子都被约了。那我们就可以通过这个特性来简化式子。
,会发现对原来的优化问题并没有影响,因子都被约了。那我们就可以通过这个特性来简化式子。
所以我们不如就让这个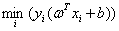 为1,即我们通过同时缩放ω和b让距离超平面最近的那些样本点的函数间隔为1,这样调整后,不仅对原来的优化问题没有影响,而且还能简化计算。
为1,即我们通过同时缩放ω和b让距离超平面最近的那些样本点的函数间隔为1,这样调整后,不仅对原来的优化问题没有影响,而且还能简化计算。
(这里缩放需要理解到位,同时缩放ω和b,会改变每个样本点到这个超平面的函数间隔,但是并不会改变每个样本点到这个超平面的几何间隔,所以我们不如就让距离这个超平面最近的那些点的函数间隔为1,简化了计算,但是也带来了约束)
但是既然设置了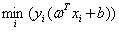 =1,那么就意味着增加了约束:
=1,那么就意味着增加了约束:
对于离超平面最近的那些样本点,它们的
对于其他的样本点,它们的
所以现在可以说:当可以找到一个超平面正确分类给定的训练集时,每个样本点的函数间隔满足:

这个就是简化所带来的约束条件
现在我们看一看简化后的优化式子变成了:
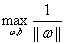
约束就是上面的对于每个样本点满足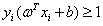
但是我们一般把这个优化问题转化为和它等价的:

而且一般会加上系数1/2,书上说是为了之后推导的方便。
所以现在我们的优化问题变成了:
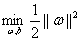
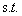
 其中i=1,2,3...m
其中i=1,2,3...m
这个就是《机器学习》书上说的SVM的基本形式。
现在整理一下推导出这个基本形式的过程:
(1)最最原始的优化目标: ,即我们需要在每个可以正确分类的平面中,找到一个到数据集的间隔最大的平面,其中间隔被定义为这个数据集样本到这个平面的最小距离
,即我们需要在每个可以正确分类的平面中,找到一个到数据集的间隔最大的平面,其中间隔被定义为这个数据集样本到这个平面的最小距离
(2)根据w和b缩放后优化目标不变,我们就可以让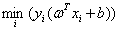 为1来简化这个问题,得到
为1来简化这个问题,得到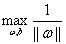 ,然后再转化为等价的
,然后再转化为等价的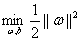
,但是注意此时就有了约束条件了!
可以看到光是得到这个最基本的形式的推导其实就有很多很多需要思考和理解的细节。
PS:谁知道如何把word上的公式方便的粘贴到网页上?必须得一个一个复制...
参考资料汇总:
[1]《机器学习》
[2]《支持向量机导论》
[3]《Pattern Recognition and Machine Learning》




