[翻译转载]OpenGL投影矩阵(Projection Matrix)构造方法
OpenGL Projection Matrix
原文地址:原文
Overview
电脑显示器是一个二维平面, 而OpenGL渲染出来的场景却是三维的 , 所以必须要投影到二维的电脑屏幕上. 可以使用 GL_PROJCETION matrix 来进行投影转换. 首先,它把顶点数据从 eye coordinates(视点坐标) 转换到 clip coordinates(裁剪坐标). 在将这些坐标除以\(w\) 坐标分量来转换到NDC(标准化设备坐标)上
因此,我们应该清楚 裁剪(可视平截头体的裁剪) 和 NDC 的转换都包含在了 GL_PROJECTION 矩阵中了. 下一段将会说明如何通过l,r,b,t,n,f(左,右,下,上,近和远)这六个边界值来构建透视矩阵.
注意 可视平截头体的裁剪(裁剪) 是在 clip coordinates(裁剪坐标) 中, 在除以 \(w_c\) 前执行的.
clip coordinates 的 \(x_c,y_c,z_c\) 会通过 \(w_c\) 来测试, 如果任何一个大于\(w_c\) 或 小于\(-w_c\), 那么这个顶点就会被丢弃.
当有丢弃时,OpenGL 将会重新构建多边形的边.
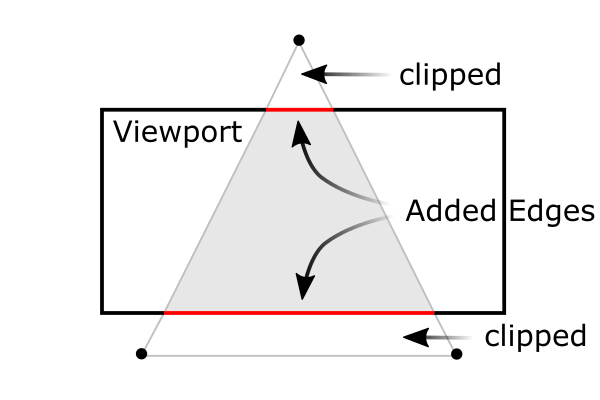
一个被平截头体剪裁的三角形
在透视投影中, truncated pyramid frustum (eye coordinates) (截锥体平截头体(视点坐标)) 中 三维的点呗映射到一个立方体(NDC); 三个坐标分量分别映射到 \([-1,1]. x: [l,r] => [-1,1], y:[b,t] => [-1,1], z:[n,f] => [-1,1]\)
注意 eye coordinates 是定义在右手坐标中的, 但 NDC 是在左手坐标中的. 因此 源点摄像机在 eye space (视觉空间) 中看向 \(z轴\) 负向 而在 NDC中 看向\(z轴\) 正向. 由于 glFrustum() 对由进到远只接受正值, 我们需要在构造 GL_PROJECTION 矩阵时 对他们取反.
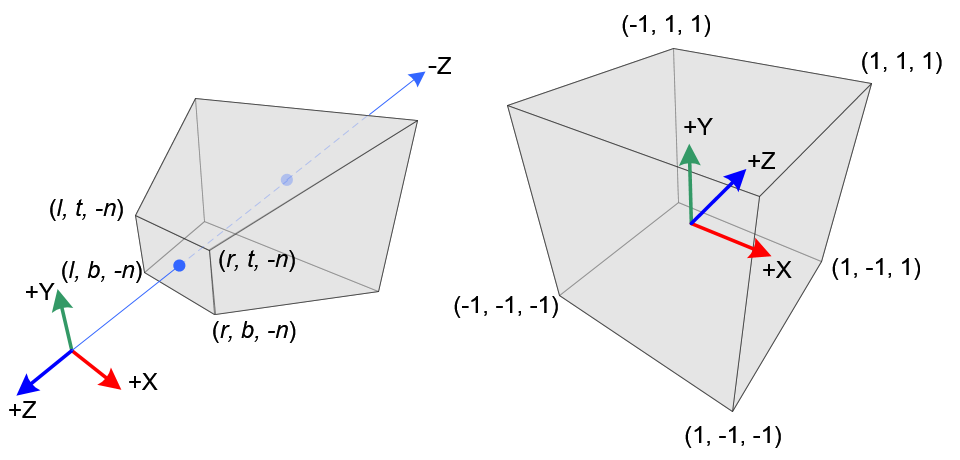
截锥体平截头体和标准化设备坐标
在OpenGL在, 在 eye space 中的三维点 会被投影到 near plane(projection plane) (近平面(投影平面)) 上, 下面这张图显示了如何将 \(p(x_e,y_e,z_e)\) 投影到 \(p(x_p,y_p,z_p)\) 上.
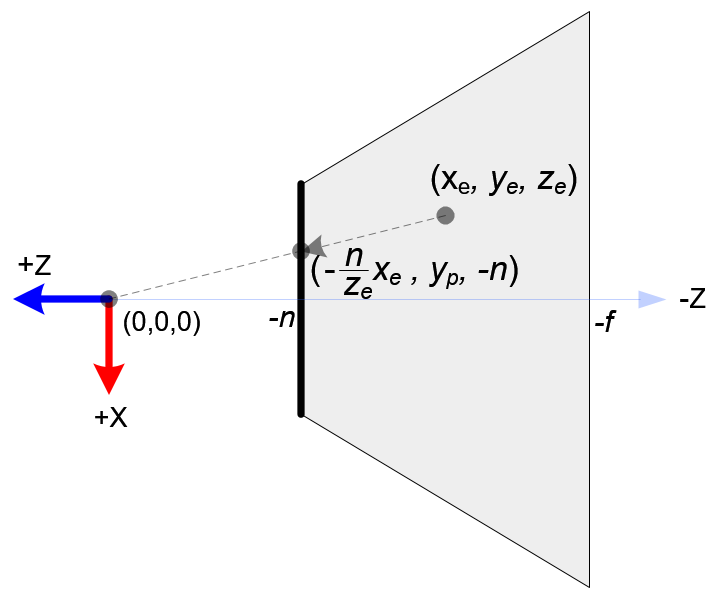
视锥体的顶视图
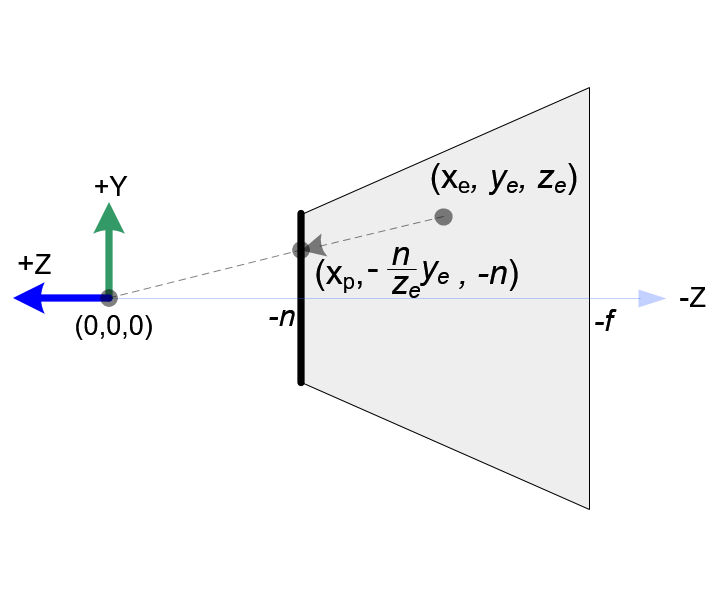
视锥体的侧视图
在顶视图中,\(x_e\),eye space 中的的x坐标, 通过相似三角形的比值的映射到 \(x_p\);
\(\frac{x_p}{x_e} = \frac{-n}{z_e}\)
\(x_p = \frac{-n*x_e}{z_e} = \frac{n*x_e}{-z_e}\)
在侧视图中,\(y_p\)也是通过相似的方法计算出来的;
\(\frac{y_p}{y_e} = \frac{-n}{z_e}\)
\(y_p = \frac{-n*y_e}{z_e} = \frac{n*y_e}{-z_e}\)
注意\(x_p和y_p\)都与\(z_e\)有关; 与\(-z_e\)成反比即除以\(-z_e\). 这是构造 GL_PROJECTION 矩阵的第一条线索. 在 eye coordinates 与 GL_PROJECTION 矩阵相乘完成变换后, clip coordinates 依然是 homogeneous coordinates(齐次坐标). 最终将其除以他的w分量来得到NDC.(更多细节OpenGL Transformation)
因此,我们可以用 \(-z_e\) 作为 clip coordinates 的 w分量. 于是 GL_PROJECTION 矩阵的第四行变成了 \((0,0,-1,0).\)
接下来,我们通过线性关系把 \(x_p,y_p\) 映射到 NDC中的\(x_n,y_n\)上; \([l,r] => [-1,1] 和 [b,t] => [-1,1]\)
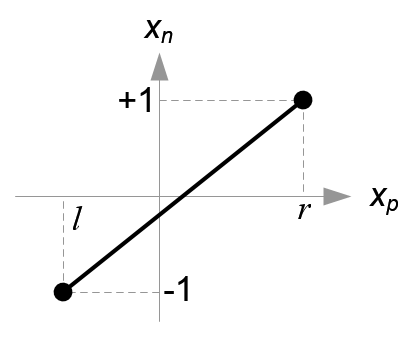
把\(x_p\)映射到\(x_n\)
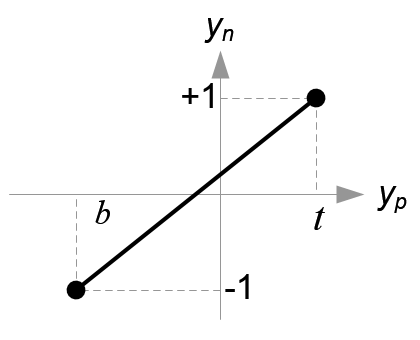
把\(y_p\)映射到\(y_n\)
然后把\(x_p和y_p变量代换到上述式子中\)
\(x_n = \frac{2x_p}{r-l}-\frac{r+l}{r-l} (x_p = \frac{nxe}{-z_e})\)
\(x_n = \frac{2*\frac{nx_e}{-z_e}}{r-l} - \frac{r+l}{r-l}\)
\(x_n = \frac{2n*x_e}{(r-l)(-z_e)} - \frac{r+l}{r-l}\)
\(x_n = \frac{\frac{2n}{r-l}*x_e}{-z_e} - \frac{r+l}{r-l}\)
\(x_n = \frac{\frac{2n}{r-l}*x_e}{-z_e} + \frac{\frac{r+l}{r-l}*z_e} {-z_e}\)
\(x_n = (\frac{2n}{r-l}*x_e+\frac{r+l}{r-l}*z_e)/-z_e = x_c / -z_e\)
同理可得
\(y_n = (\frac{2n}{t-b}*y_e+\frac{t+b}{t-b}*z_e)/-z_e = y_c/-z_e\)
注意我们使每个方程的两个项都除以\(-z_e\) 来表示perspective division(透视除法)(\(x_c/w_c,y_c/w_c\)). 而且我们之前已经把\(w_c设成了-z_e\)了, 所以括号内的项已经是 clip coordinates 的 \(x_c和y_c\)了.
于是得到了GL_PROJECTION 矩阵的前两行
现在我们只剩GL_PROJECTION 矩阵的第三行需要解出了. 但解\(z_n\)并不像其他坐标那样简单,因为 eye space 的\(z_e\)总是被投影到近平面的-n上. 但我们为了 clipping(裁剪)和 depth test(深度测试)需要保证z坐标的唯一性.,而且还要能够反投影(还原变换). 因为z并不依赖于x和y坐标,我们借用w分量 来找到 \(z_n和z_e\)之间的关系. 因此我们可以像下面这样来指定 GL_PROJECTION 矩阵的第三行.
在 eye space中, \(w_e\) 等于1. 因此等式变成
\(z_n = \frac{Az_e+B}{-z_e}\)
我们用(\(z_e,z_n)\)的关系来找到系数A和B;将\((-n,-1)和(-f,1)\)回代到上式中
\(\left\{\begin{matrix}
\frac{-An+B}{n} = -1\\
\frac{-Af+B}{f} = 1
\end{matrix}\right. \rightarrow
\left\{\begin{matrix}
-An+B = -n \;(1)\\
-Af+B = f \;(2)
\end{matrix}\right.\)
重写等式(1);
\(B=An-n \; (1')\)
将B带入(2);
\(-Af +(An-n) = f \; (2)\)
$-(f-n)A = f + n \(
\)A = -\frac{f+n}{f-n}$
把A回代到(1)中;
\((\frac{f+n}{f-n})n + B = -n \; (1)\)
\(B = -n - (\frac{f+n}{f-n})n = -(1+\frac{f+n}{f-n})n = -(\frac{f-n+f+n}{f-n})n = -\frac{2fn}{f-n}\)
解出A和B后就可以得到\(Z_e和Z_n\)的关系;
\(Z_n = \frac{-\frac{f+n}{f-n}z_e - \frac{2fn}{f-n}}{-z_e} \; (3)\)
最终解出了整个 GL_PROJECTION 矩阵
这个投影矩阵是一种通用形式,如果可视平截头体是对称的,即\(r=-l 和 t=-b\),可以对其化简
在继续之前,请观察一下等式(3)中\(z_e和z_n\)的关系,你会发现他们并不是线性关系而是分式关系,这意味着在近平面会有非常高的精度而远平面的精度很低.如果\([-n,-f]\)的范围很大,就会导致深度精度问题(z-fighting(深度冲突)); 在远平面\(z_e\)值小改动不会影响到\(z_n\)的值. 所以\(n和f\)的距离应该越小越好从而减少深度缓冲的精度问题.
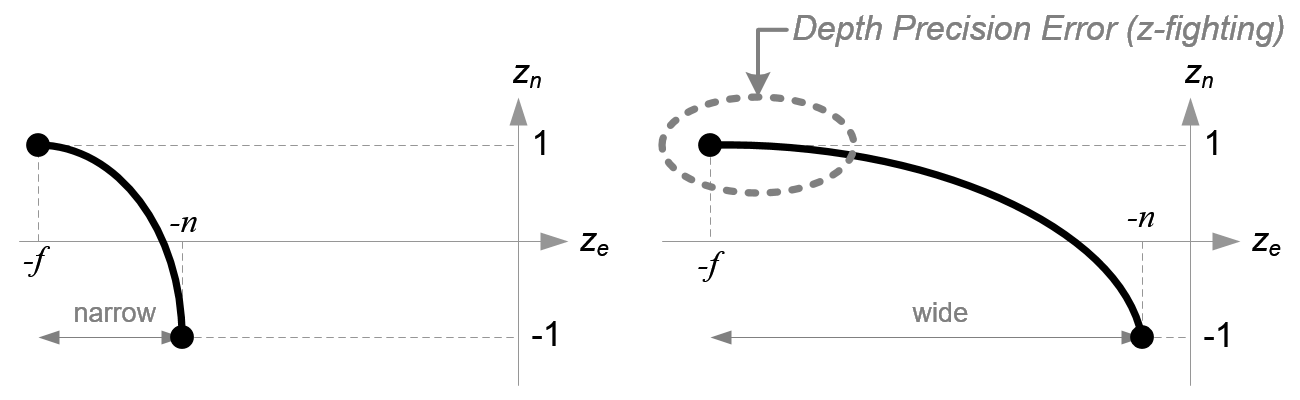
深度缓冲精度的比较
Orthographic Projection(正射投影)
为正射投影构造 GL_PROJECTION 矩阵 比透视模式下的要简单的多
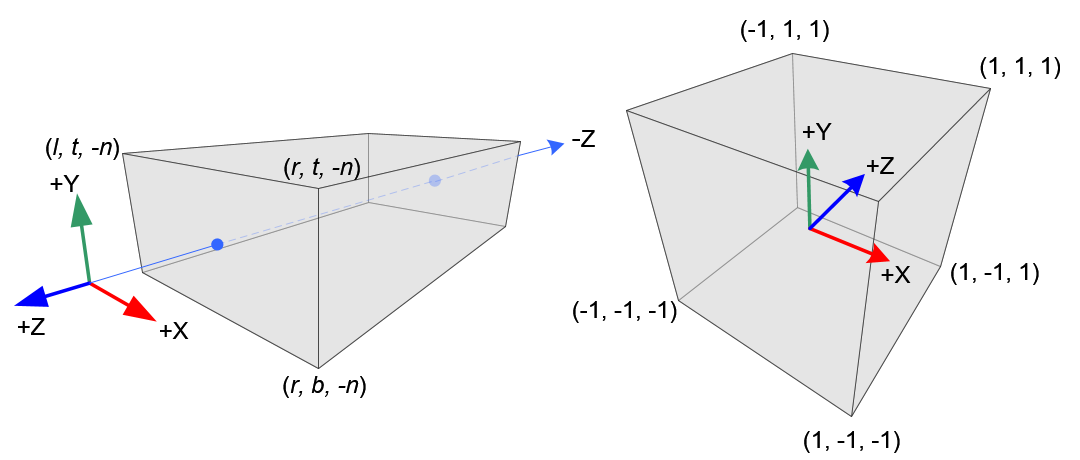
正射视锥和标准化设备坐标(NDC)
eye space 中所有的\(x_e,y_e和z_e\)分量都线性映射到 NDC. 我们只需要把长方体视锥缩放正方体,然后把它移动到原点. 让我们来通过线性关系来解出 GL_PROJECTION 里的元素吧.
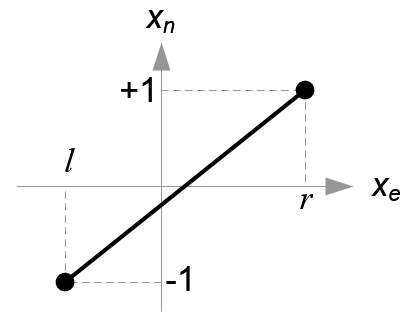
把\(x_e映射到x_n\)
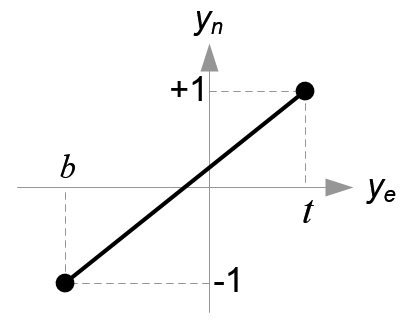
把\(y_e映射到y_n\)
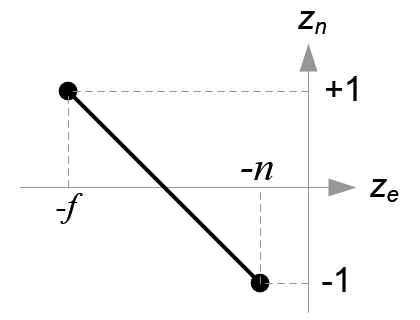
把\(z_e映射到z_n\)
由于在正射投影中不再需要w分量, GL_PROJECTION 矩阵的第四行 保留成(0,0,0,1), 于是可以得到 正射投影的 GL_PROJECTION 矩阵
同样的,如果视锥是对称的,即\(r=-l 和 t=-b\),可以对其化简

