机器学习--深度学习基本概念

根据李宏毅老师机器学习课程所做的笔记。

函数y=wx+b，输入与输出之间是一个线性的关系。改变w可以改变直线的斜率，改变b可以改变直线的截距。

 

 

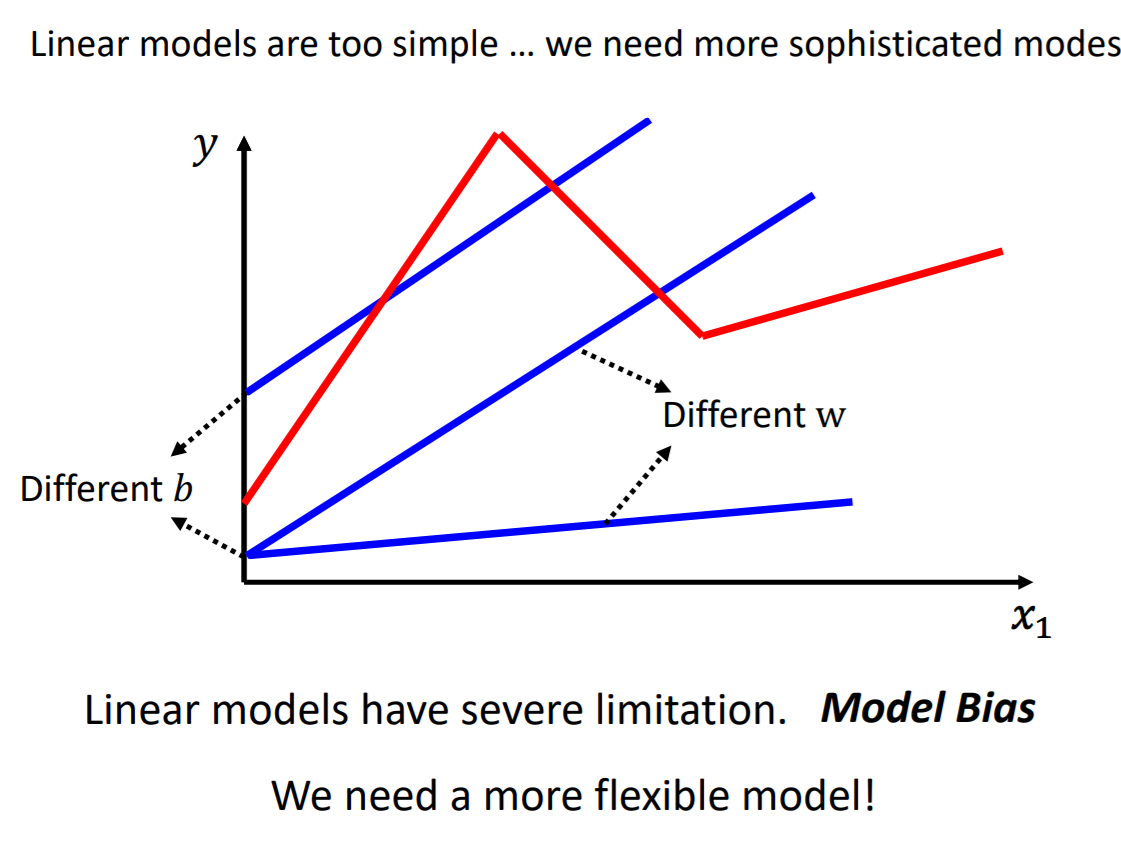
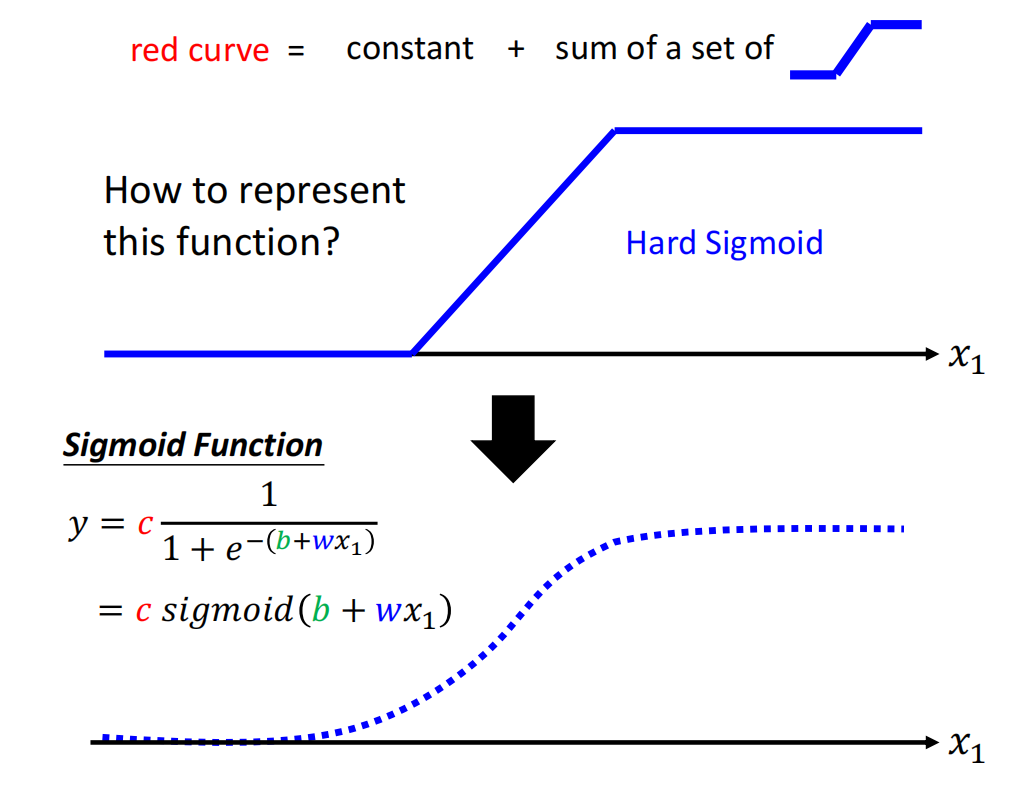
 但是如果想要刻画上图中的红色直线是困难的。这条红色的曲线应该怎么表示呢？

 

 

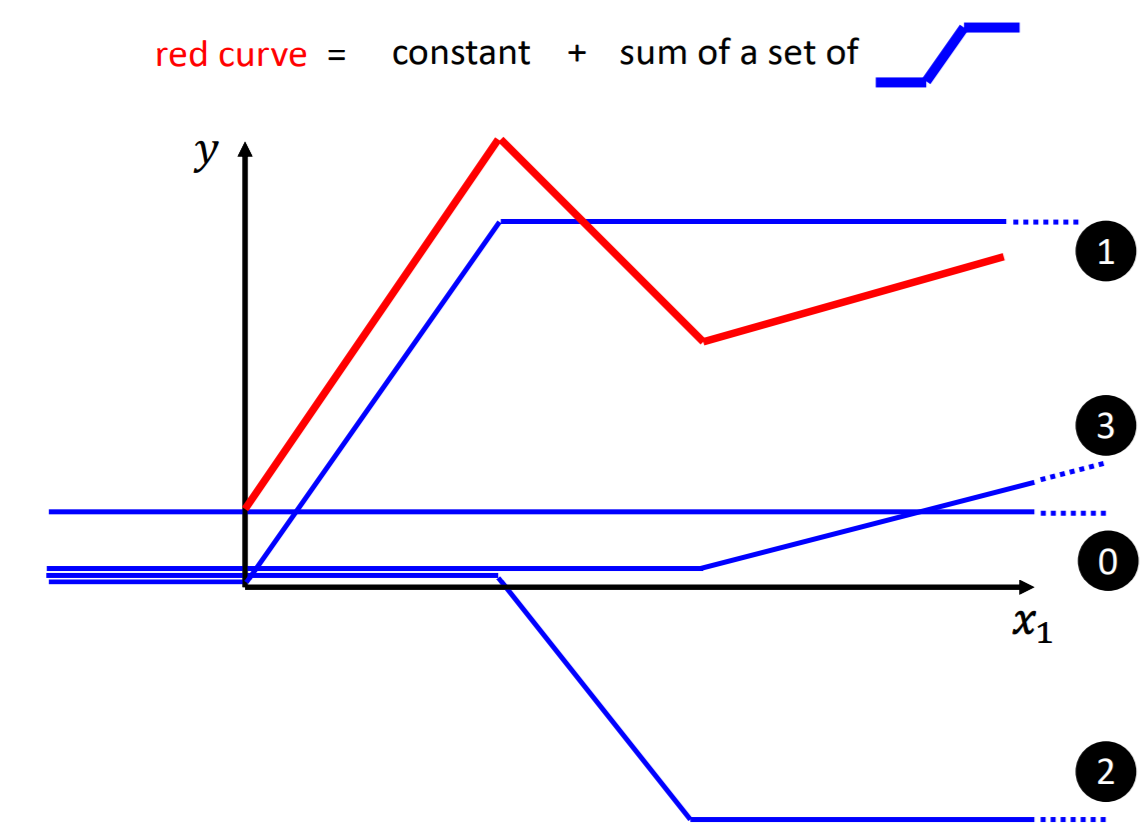
 红色的曲线可以表示为图中蓝色曲线的和。

蓝色曲线(Hard Sigmoid)的特征是拥有两个转折点threshold1和threshold2，小于threshold1和大于threshold2的部分取一个定值，两个转折点中间是一条线段（一个斜坡）。

 

 

 

 

 

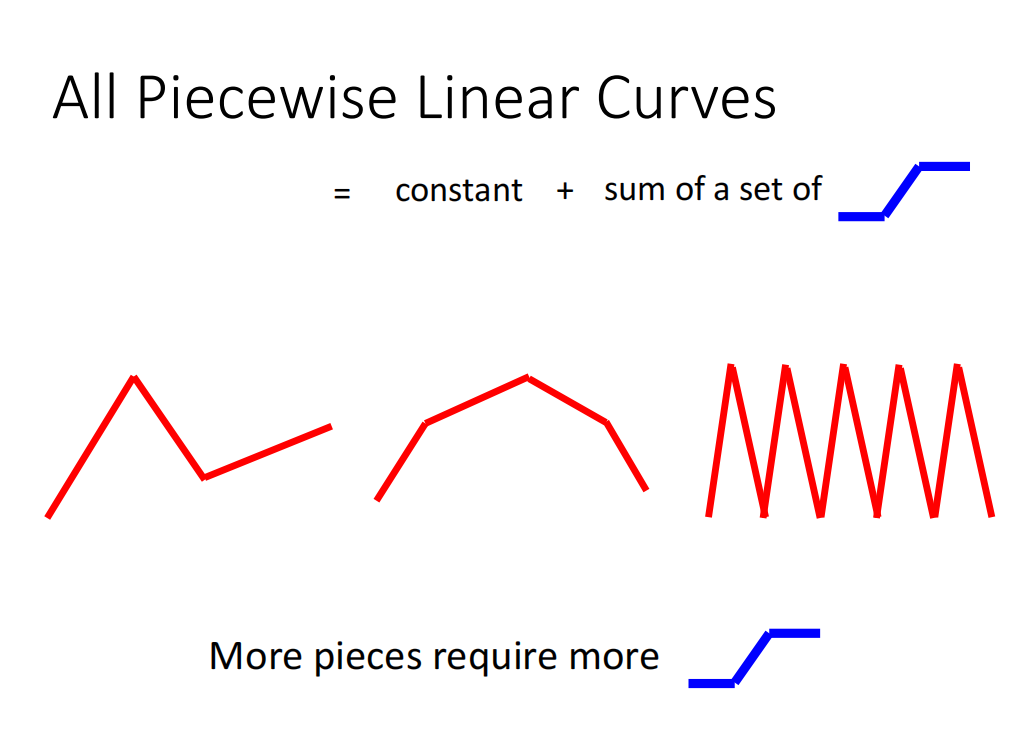
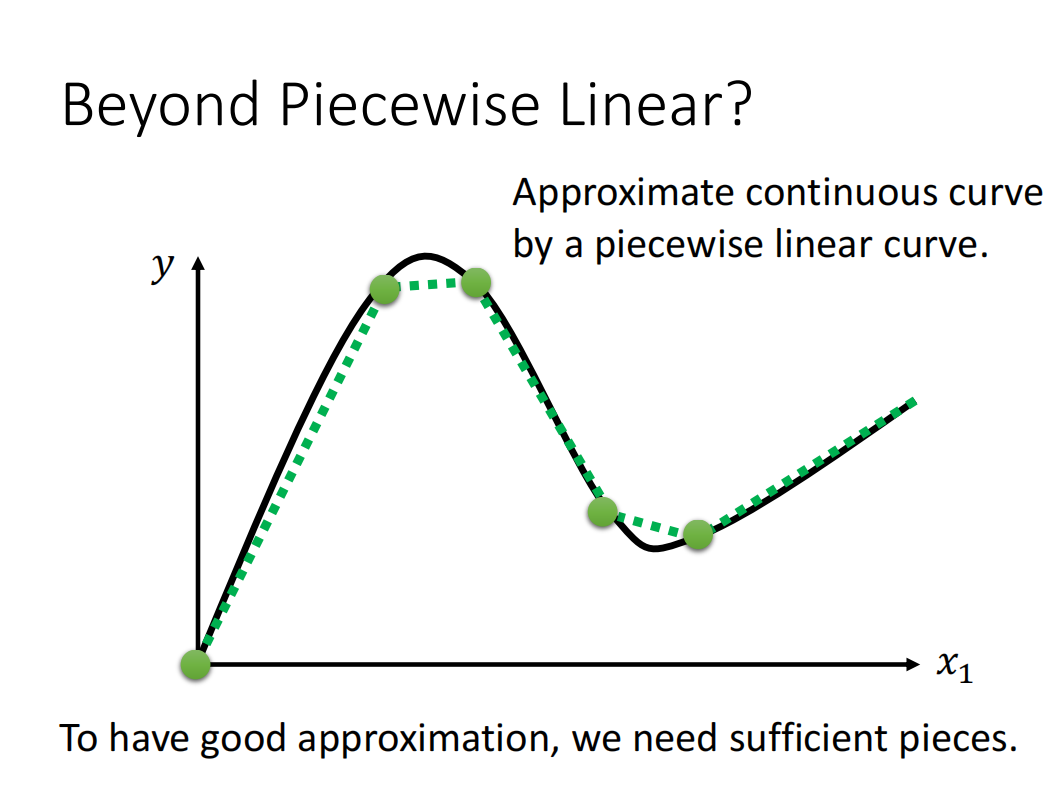
 如果函数的形状不是直线，而是曲线，也可以用直线来近似这条曲线。

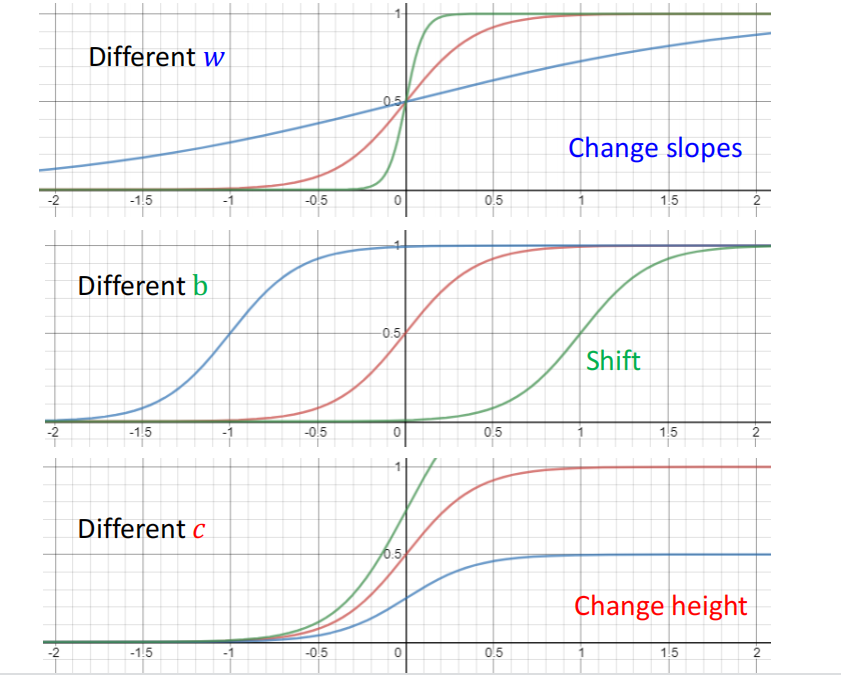
怎么表示上面的蓝色直线呢？我们使用sigmoid函数来近似它。c是它的系数。取值范围是(0,c)。

 

 

 

 

 由此，可以使用sigmoid函数的组合来近似我们想要的函数。

以上面的红色曲线为例，将1，2，3这三条曲线用sigmoid函数来表示，b代表直线0。y的表达式如下图所示。

 

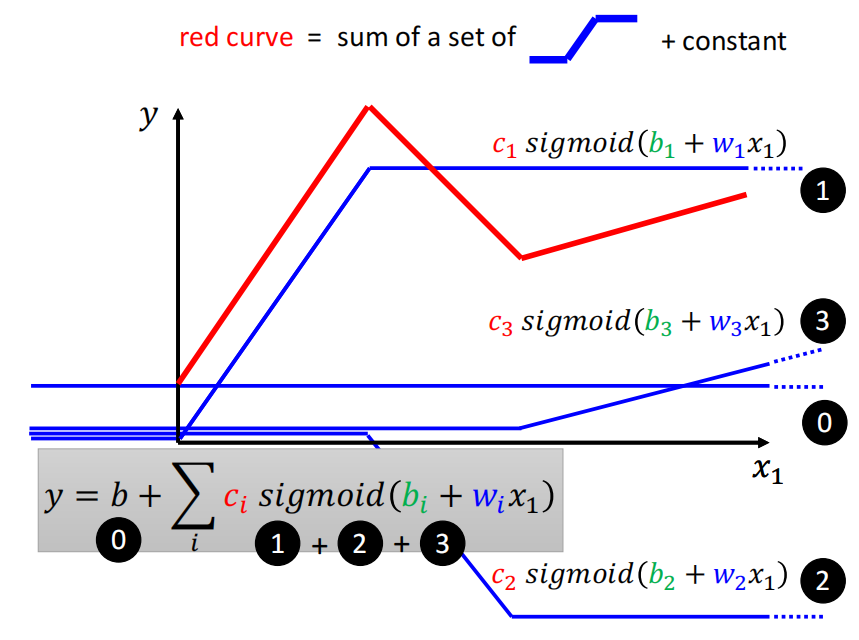
 如果有更多的特征输入，y的表达式如下所示。

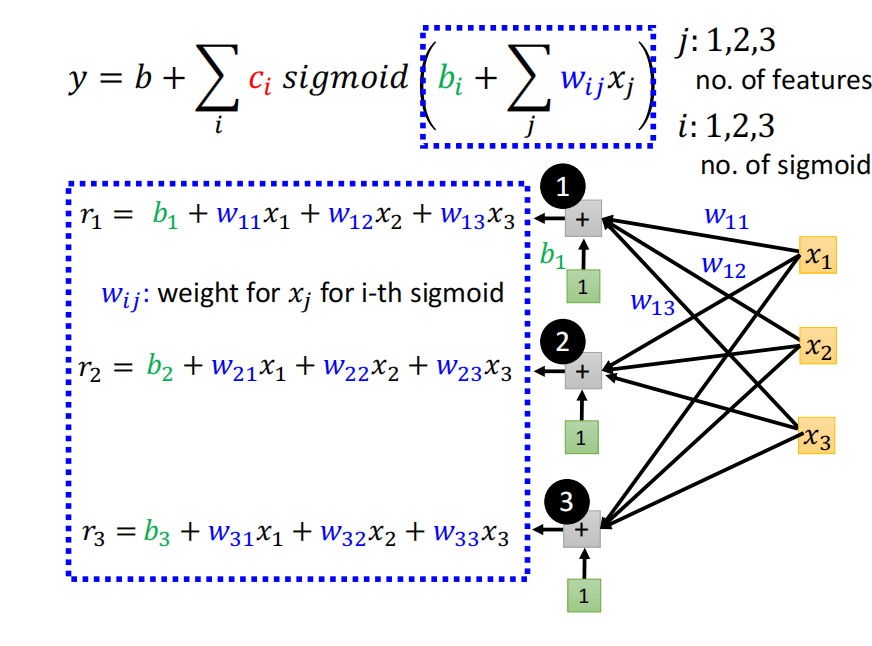
使用矩阵对公式进行简化。

 

 

 

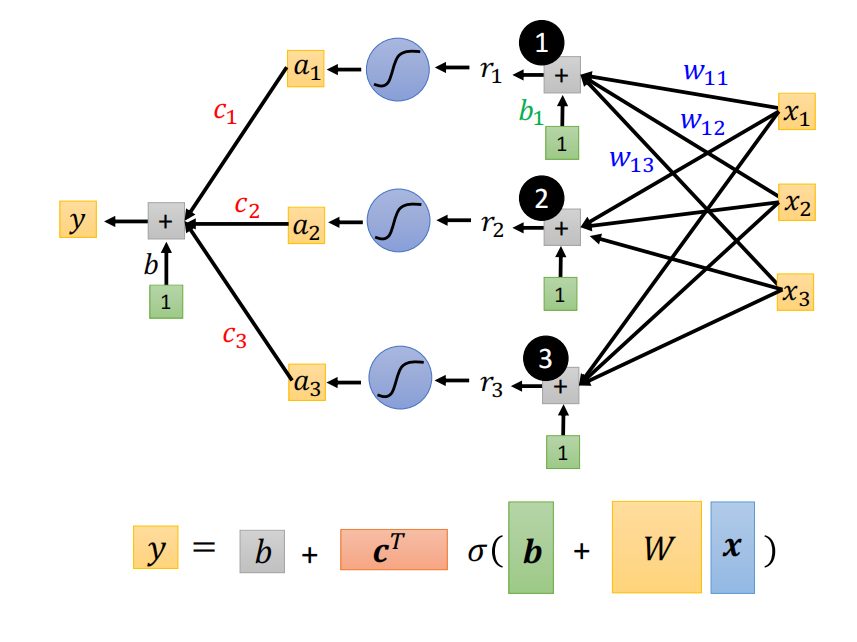
所有未知的参数都统称为theta。

 

 

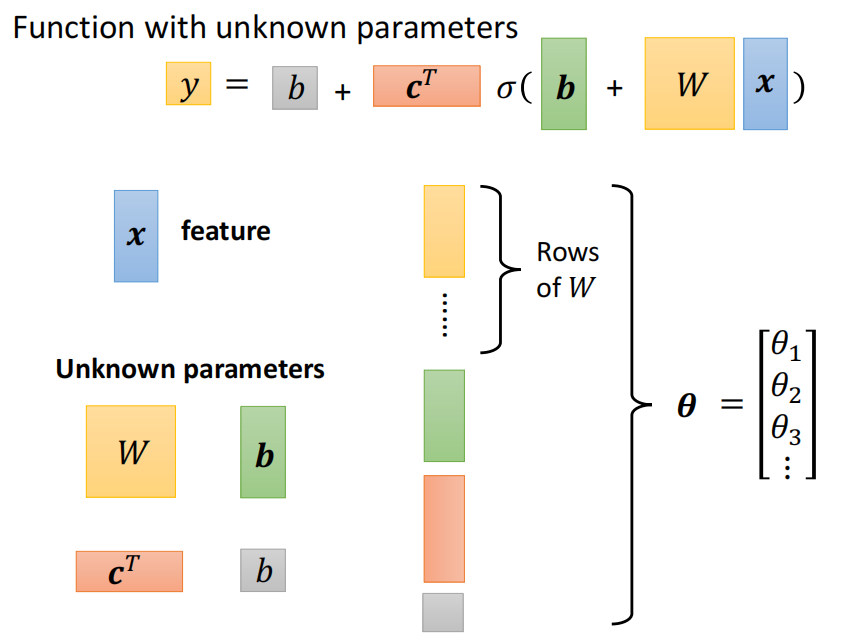
 到这里，我们已经定义了含有未知参数的函数，下一步似乎定义损失函数。

 

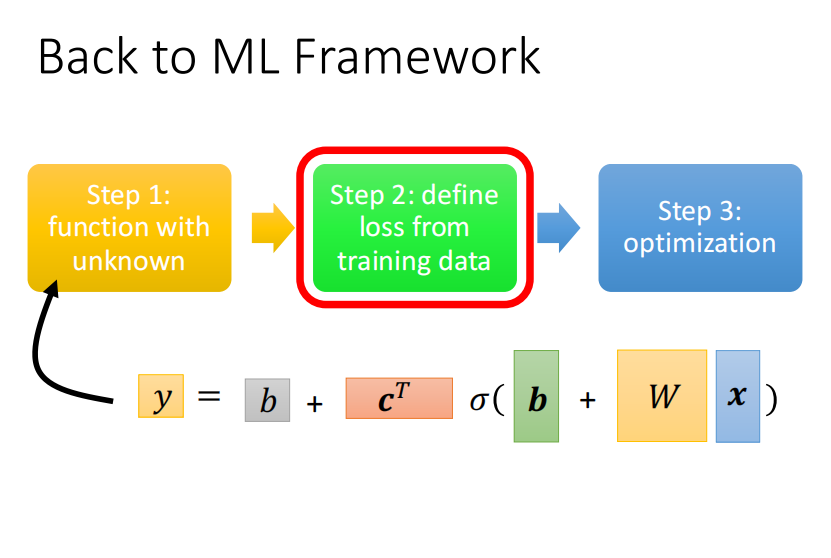
 损失函数的定义如下。

 

 

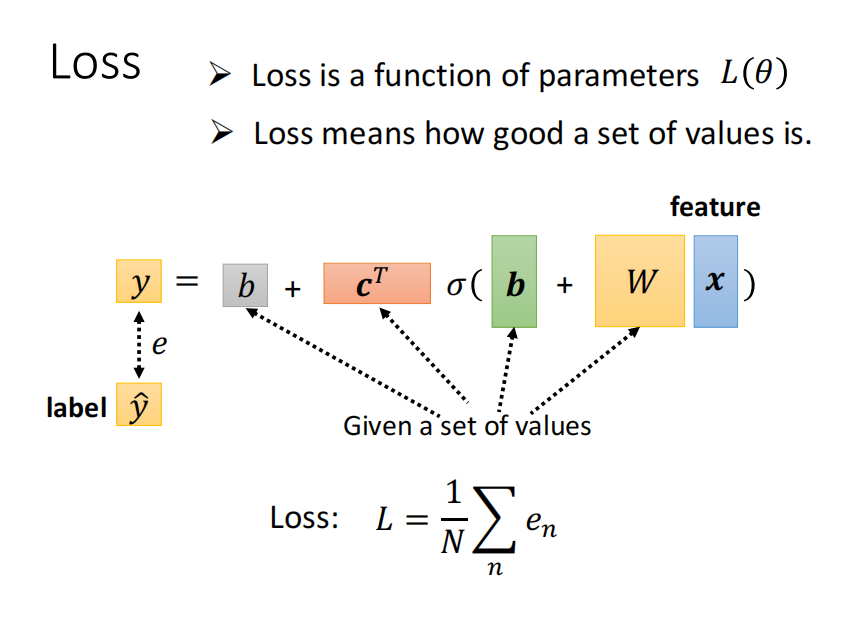
 下面使用梯度下降算法来优化损失函数。

根据求导的结果来更新参数。

 

 

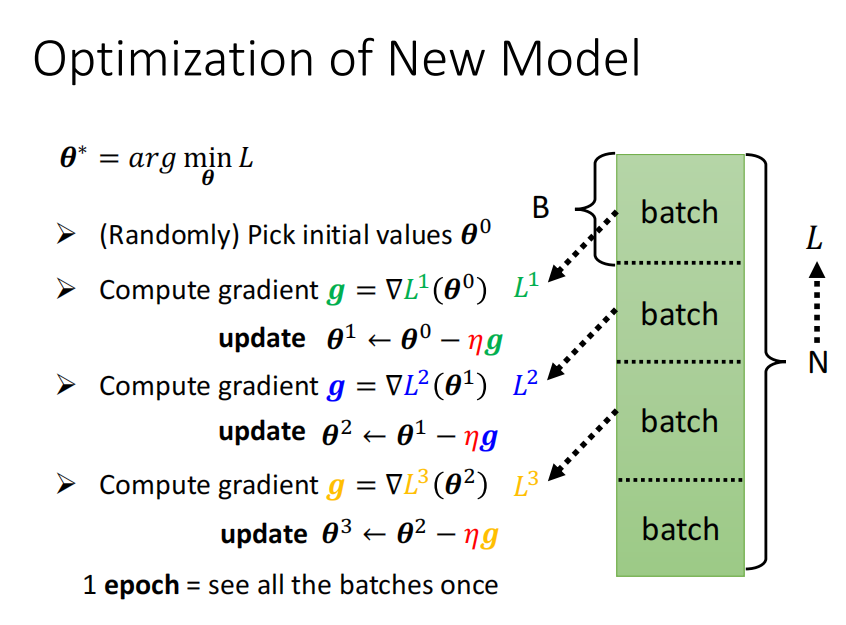
 在进行优化时，对数据分成一个一个批次，每次只拿出一个批次来计算L1，根据这个L1来计算gradient，再用这个gradient更新参数。

下一次，选取下一个批次来计算L2，...，直至所有地批次都计算结束。当所有的批次都参与一次计算后，这个过程成为一个Epoch。

 

 

下面介绍对模型做一些变形的情况。

上面都是用sigmoid组成我们想要的函数，其实也可以用别的函数。Hard sigmoid也可以看成是两个ReLU函数的和。

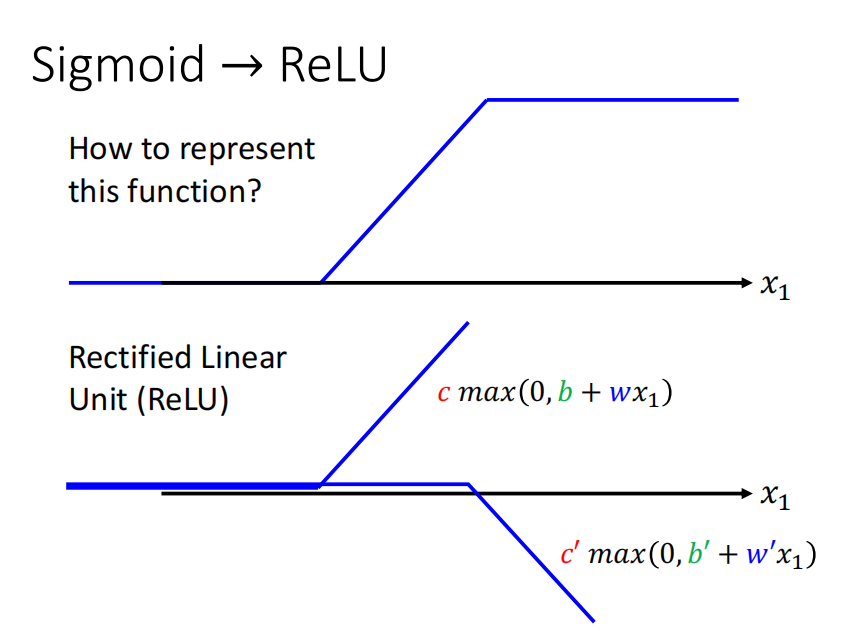
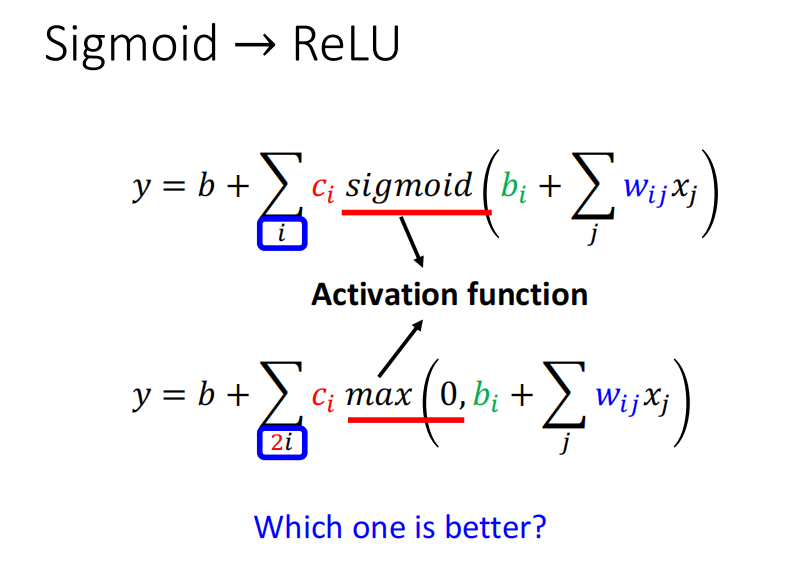
 sigmoid和ReLU在机器学习中被成为激活函数。一般使用ReLU更多。

 接着可以再对模型进行改进。将a作为下一层的输入继续计算。

 

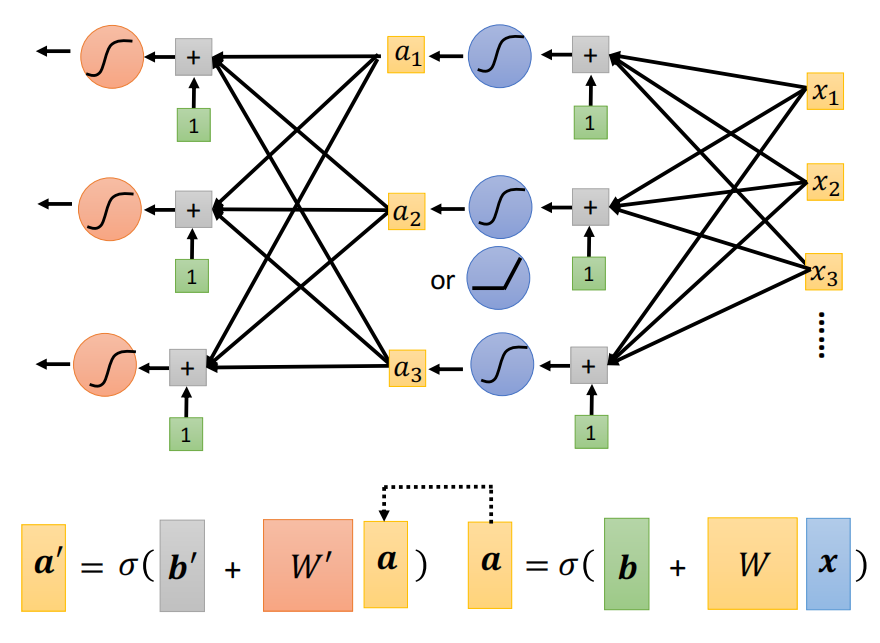
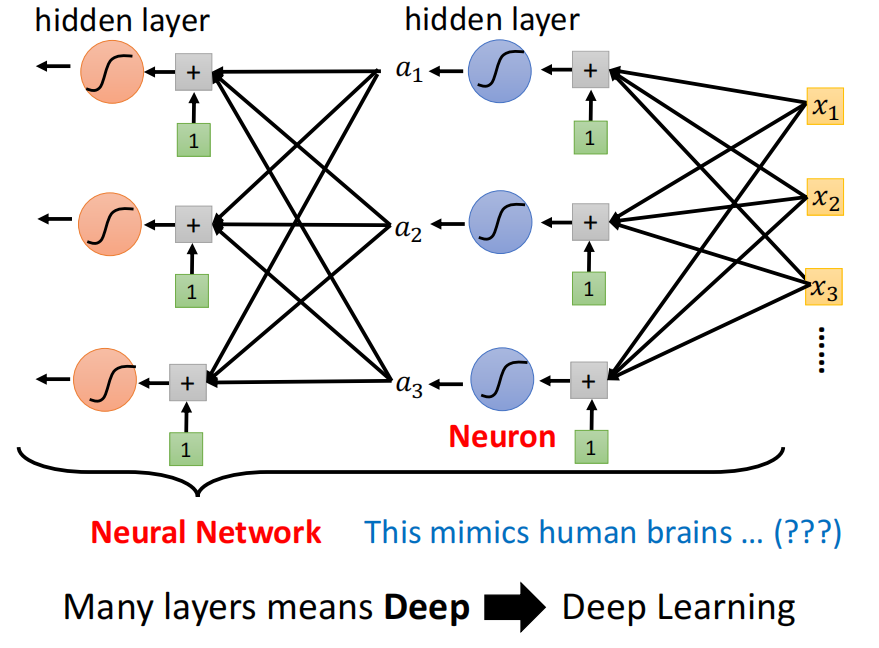
 一个sigmoid或者ReLU的处理称为是一个神经元(Neuron)，许多的神经元组成神经网络(Neural Network)。

上图中一列神经元叫做一层，有很多层组成，体现了它的深度，整个过程也被称为深度学习。