二十一、所有结点对最短路径问题(弗洛伊德算法)
弗洛伊德算法介绍
和Dijkstra算法一样,弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
基本思想
通过Floyd计算图G=(V,E)中各个顶点的最短路径时,需要引入一个矩阵S,矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。
假设图G中顶点个数为N,则需要对矩阵S进行N次更新。初始时,矩阵S中顶点a[i][j]的距离为顶点i到顶点j的权值;如果i和j不相邻,则a[i][j]=∞。 接下来开始,对矩阵S进行N次更新。第1次更新时,如果"a[i][j]的距离" > "a[i][0]+a[0][j]"(a[i][0]+a[0][j]表示"i与j之间经过第1个顶点的距离"),则更新a[i][j]为"a[i][0]+a[0][j]"。 同理,第k次更新时,如果"a[i][j]的距离" > "a[i][k]+a[k][j]",则更新a[i][j]为"a[i][k]+a[k][j]"。更新N次之后,操作完成!
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
弗洛伊德算法图解
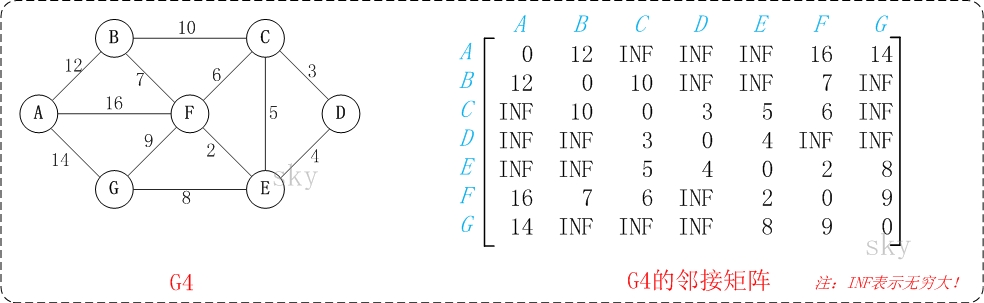
以上图G4为例,来对弗洛伊德进行算法演示。
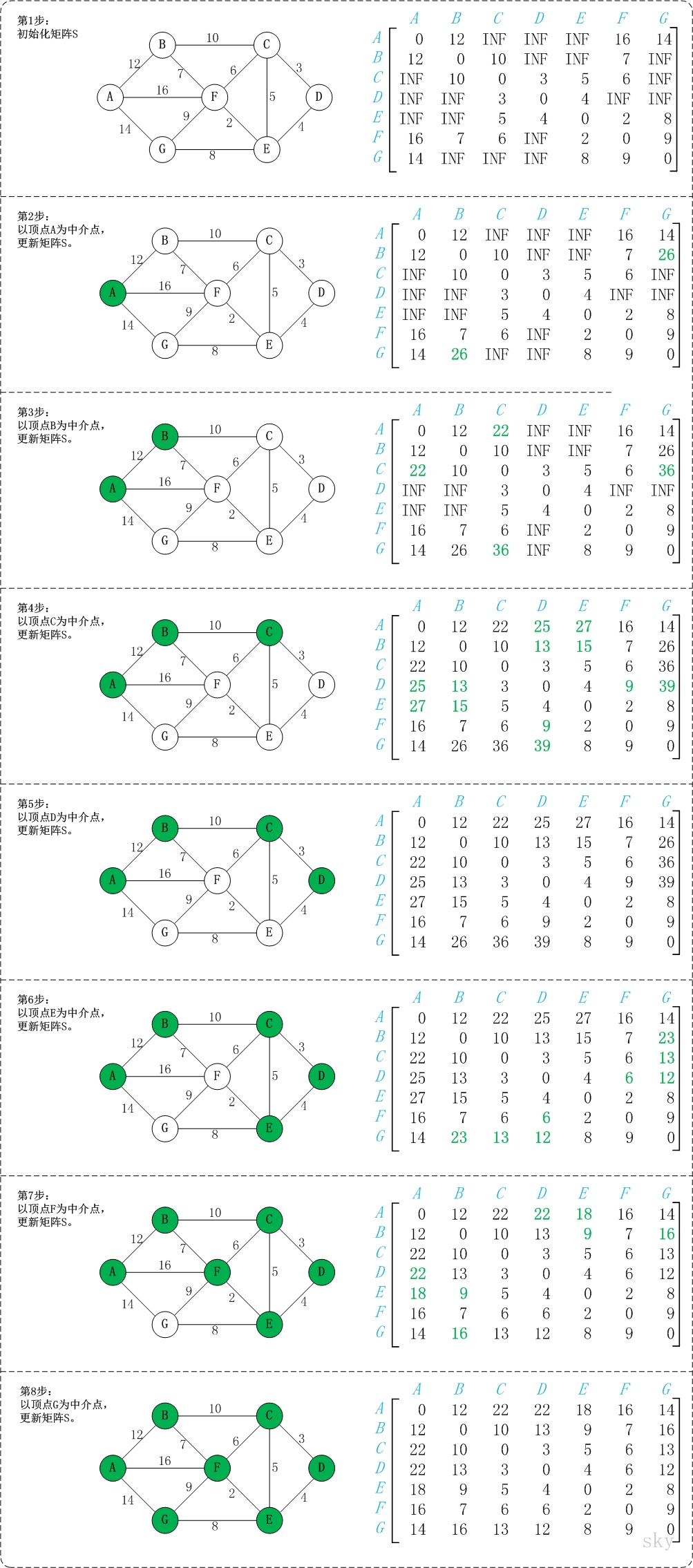
初始状态:S是记录各个顶点间最短路径的矩阵。
第1步:初始化S。
矩阵S中顶点a[i][j]的距离为顶点i到顶点j的权值;如果i和j不相邻,则a[i][j]=∞。实际上,就是将图的原始矩阵复制到S中。
注:a[i][j]表示矩阵S中顶点i(第i个顶点)到顶点j(第j个顶点)的距离。
第2步:以顶点A(第1个顶点)为中介点,若a[i][j] > a[i][0]+a[0][j],则设置a[i][j]=a[i][0]+a[0][j]。
以顶点a[1]6,上一步操作之后,a[1][6]=∞;而将A作为中介点时,(B,A)=12,(A,G)=14,因此B和G之间的距离可以更新为26。
同理,依次将顶点B,C,D,E,F,G作为中介点,并更新a[i][j]的大小。
邻接矩阵:
class Vertex
{
public char label;
public boolean wasVisited;
public Vertex(char lab)
{
label = lab;
wasVisited = false;
}
}
class DGraph
{
private final int MAX_VERTS = 20;
private Vertex vertexList[];
private int adjMat[][];
private int nVerts;
public DGraph()
{
vertexList = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for(int i=0;i<MAX_VERTS;i++)
for(int j=0;j<MAX_VERTS;j++)
if(i!=j)
adjMat[i][j] = Integer.MAX_VALUE;
else
adjMat[i][j] = 0;
}
public void addVertex(char lab)
{
vertexList[nVerts++] = new Vertex(lab);
}
public void addEdge(int start,int end,int weight)
{
adjMat[start][end] = weight;
//去掉就是有向图
//adjMat[end][start] = weight;//无向图
}
/*
* floyd最短路径。
* 即,统计图中各个顶点间的最短路径。
*
* 参数说明:
* path -- 路径。path[i][j]=k表示,"顶点i"到"顶点j"的最短路径会经过顶点k。
* dist -- 长度数组。即,dist[i][j]=sum表示,"顶点i"到"顶点j"的最短路径的长度是sum。
*/
public void Floyd()
{
int dist[][] = new int[nVerts][nVerts];
int path[][] = new int[nVerts][nVerts];
//初始化
for(int i=0;i<nVerts;i++)
{
for(int j=0;j<nVerts;j++)
{
dist[i][j] = adjMat[i][j];
path[i][j] = -1;
}
}
// 完成以k为中间点对所有矩阵dist[i][j]的顶点对{i,j}进行检测和修改。
// 如果经过下标为k顶点路径比原两点间路径更短,则更新dist[i][j]和path[i][j]
for(int k=0;k<nVerts;k++)
for(int i = 0;i<nVerts;i++)
for(int j=0;j<nVerts;j++)
{
//顶点i与顶点k连接且顶点j与顶点k连接且经过下标为k顶点路径比原两点间路径更短
if(dist[i][k] != Integer.MAX_VALUE && dist[k][j] !=Integer.MAX_VALUE &&
dist[i][k]+dist[k][j]<dist[i][j])
{
dist[i][j] = dist[i][k]+dist[k][j];
path[i][j] = k;
}
}
System.out.println("floyd最短路径结果:");
for(int i=0;i<nVerts;i++)
{
for(int j=0;j<nVerts;j++)
{
if(i!=j)
{
int k = path[i][j];
System.out.print("顶点"+vertexList[i].label+"到顶点"+vertexList[j].label+
"的路径:"+vertexList[i].label);
while(k!=-1)
{
System.out.print(vertexList[k].label);
k = path[k][j];
}
System.out.println(vertexList[j].label+" 最短路径长度:"+dist[i][j]);
}
}
}
}
}
public class MatrixDG_Floyd
{
public static void main(String[] args)
{
DGraph theGraph = new DGraph();
theGraph.addVertex('A'); // 0
theGraph.addVertex('B'); // 1
theGraph.addVertex('C'); // 2
theGraph.addVertex('D'); // 3
theGraph.addEdge(0, 1,5); // AB
theGraph.addEdge(0, 3,7); // AD
theGraph.addEdge(1, 2,4); // BC
theGraph.addEdge(1, 3,2); // BD
theGraph.addEdge(2, 3,2); // CD
theGraph.addEdge(2, 0,3); // CA
theGraph.addEdge(2, 1,3); // CB
theGraph.addEdge(3, 2,1); // DC
theGraph.Floyd();
}
}
floyd最短路径结果:
顶点A到顶点B的路径:AB 最短路径长度:5
顶点A到顶点C的路径:ADC 最短路径长度:8
顶点A到顶点D的路径:AD 最短路径长度:7
顶点B到顶点A的路径:B 最短路径长度:6
顶点B到顶点C的路径:BDC 最短路径长度:3
顶点B到顶点D的路径:BD 最短路径长度:2
顶点C到顶点A的路径:CA 最短路径长度:3
顶点C到顶点B的路径:CB 最短路径长度:3
顶点C到顶点D的路径:CD 最短路径长度:2
顶点D到顶点A的路径:DCA 最短路径长度:4
顶点D到顶点B的路径:DCB 最短路径长度:4
顶点D到顶点C的路径:DC 最短路径长度:1
邻接链表:
class Vertex
{ public char label; public boolean wasVisited; public Edge firstEdge; public Vertex(char lab)
{ this.label = lab; this.wasVisited = false; firstEdge = null; } } class Edge
{ public int dest; public int weight; public Edge nextEdge; public Edge(int dest,int weight)
{ this.dest= dest; this.weight = weight; nextEdge = null; } } class DGraph
{ private final int MAX_VERTS = 20;//图的最大顶点数 private int nVerts = 0;//当前顶点数 private Vertex vertexList[];//顶点链表 public DGraph()
{ vertexList = new Vertex[MAX_VERTS]; } public void addVertex(char lab)
{ vertexList[nVerts++] = new Vertex(lab); } public void addEdge(int start,int end,int weight)
{ Edge endEdge = new Edge(end,weight); Edge edge2 = vertexList[start].firstEdge; if(edge2==null)
{ vertexList[start].firstEdge = endEdge; }else
{ while(edge2.nextEdge!=null) edge2 = edge2.nextEdge; edge2.nextEdge = endEdge; } } /* * floyd最短路径。 * 即,统计图中各个顶点间的最短路径。 * * 参数说明: * path -- 路径。path[i][j]=k表示,"顶点i"到"顶点j"的最短路径会经过顶点k。 * dist -- 长度数组。即,dist[i][j]=sum表示,"顶点i"到"顶点j"的最短路径的长度是sum。 */ public void Floyd(){ int dist[][] = new int[nVerts][nVerts]; int path[][] = new int[nVerts][nVerts]; //初始化 for(int i=0;i<nVerts;i++)
{ for(int j=0;j<nVerts;j++)
{ dist[i][j] = getWeight(i, j); path[i][j] = -1; } } // 完成以k为中间点对所有矩阵dist[i][j]的顶点对{i,j}进行检测和修改。 // 如果经过下标为k顶点路径比原两点间路径更短,则更新dist[i][j]和path[i][j] for(int k=0;k<nVerts;k++) for(int i = 0;i<nVerts;i++) for(int j=0;j<nVerts;j++)
{ //顶点i与顶点k连接且顶点j与顶点k连接且经过下标为k顶点路径比原两点间路径更短 if(dist[i][k] != Integer.MAX_VALUE && dist[k][j] !=Integer.MAX_VALUE &&
dist[i][k]+dist[k][j]<dist[i][j])
{ dist[i][j] = dist[i][k]+dist[k][j]; path[i][j] = k; } } System.out.println("floyd最短路径结果:"); for(int i=0;i<nVerts;i++)
{ for(int j=0;j<nVerts;j++)
{ if(i!=j)
{ int k = path[i][j]; System.out.print("顶点"+vertexList[i].label+"到顶点"+vertexList[j].label+
"的路径:"+vertexList[i].label); while(k!=-1)
{ System.out.print(vertexList[k].label); k = path[k][j]; } System.out.println(vertexList[j].label+" 最短路径长度:"+dist[i][j]); } } } } /* * 获取边<start, end>的权值;若start和end不是连通的,则返回无穷大。 */ private int getWeight(int start, int end)
{ if (start==end) return 0; Edge currentEdge = vertexList[start].firstEdge; while (currentEdge != null)
{ if (end==currentEdge.dest) return currentEdge.weight; currentEdge = currentEdge.nextEdge; } return Integer.MAX_VALUE; } } public class ListDG_Floyd
{ public static void main(String[] args)
{ DGraph theGraph = new DGraph(); theGraph.addVertex('A'); // 0 theGraph.addVertex('B'); // 1 theGraph.addVertex('C'); // 2 theGraph.addVertex('D'); // 3 theGraph.addEdge(0, 1,5); // AB theGraph.addEdge(0, 3,7); // AD theGraph.addEdge(1, 2,4); // BC theGraph.addEdge(1, 3,2); // BD theGraph.addEdge(2, 3,2); // CD theGraph.addEdge(2, 0,3); // CA theGraph.addEdge(2, 1,3); // CB theGraph.addEdge(3, 2,1); // DC theGraph.Floyd(); } }
floyd最短路径结果:
顶点A到顶点B的路径:AB 最短路径长度:5
顶点A到顶点C的路径:ADC 最短路径长度:8
顶点A到顶点D的路径:AD 最短路径长度:7
顶点B到顶点A的路径:B 最短路径长度:6
顶点B到顶点C的路径:BDC 最短路径长度:3
顶点B到顶点D的路径:BD 最短路径长度:2
顶点C到顶点A的路径:CA 最短路径长度:3
顶点C到顶点B的路径:CB 最短路径长度:3
顶点C到顶点D的路径:CD 最短路径长度:2
顶点D到顶点A的路径:DCA 最短路径长度:4
顶点D到顶点B的路径:DCB 最短路径长度:4
顶点D到顶点C的路径:DC 最短路径长度:1


