十七、拓扑排序
拓扑排序介绍
拓扑排序(Topological Order)是指,将一个有向无环图(Directed Acyclic Graph简称DAG)进行排序进而得到一个有序的线性序列。
这样说,可能理解起来比较抽象。下面通过简单的例子进行说明!
例如,一个项目包括A、B、C、D四个子部分来完成,并且A依赖于B和D,C依赖于D。现在要制定一个计划,写出A、B、C、D的执行顺序。这时,就可以利用到拓扑排序,它就是用来确定事物发生的顺序的。
在拓扑排序中,如果存在一条从顶点A到顶点B的路径,那么在排序结果中B出现在A的后面。
拓扑排序的算法图解
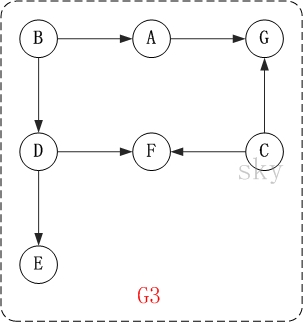
以上图为例,来对拓扑排序进行演示。

第1步:将B和C加入到排序结果中。
顶点B和顶点C都是没有依赖顶点,因此将C和C加入到结果集T中。假设ABCDEFG按顺序存储,因此先访问B,再访问C。访问B之后,去掉边<B,A>和<B,D>,并将A和D加入到队列Q中。同样的,去掉边<C,F>和<C,G>,并将F和G加入到Q中。
(01) 将B加入到排序结果中,然后去掉边<B,A>和<B,D>;此时,由于A和D没有依赖顶点,因此并将A和D加入到队列Q中。
(02) 将C加入到排序结果中,然后去掉边<C,F>和<C,G>;此时,由于F有依赖顶点D,G有依赖顶点A,因此不对F和G进行处理。
第2步:将A,D依次加入到排序结果中。
第1步访问之后,A,D都是没有依赖顶点的,根据存储顺序,先访问A,然后访问D。访问之后,删除顶点A和顶点D的出边。
第3步:将E,F,G依次加入到排序结果中。
因此访问顺序是:B -> C -> A -> D -> E -> F -> G
邻接矩阵:
class Vertex
{
public char label;
public Vertex(char lab)
{
label = lab;
}
}
class DGraph
{
private final int MAX_VERTS = 20;
private int nVerts;
private Vertex vertexList[];
private int adjMat[][];
private char sortedArray[];
public DGraph()
{
vertexList = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for(int i=0;i<MAX_VERTS;i++)
for(int j=0;j<MAX_VERTS;j++)
adjMat[i][j] = 0;
sortedArray = new char[MAX_VERTS];
}
public void addVertex(char lab)
{
vertexList[nVerts++] = new Vertex(lab);
}
public void addEdge(int start,int end)
{
adjMat[start][end] = 1;
}
public void displayVertex(int v)
{
System.out.println(vertexList[v].label);
}
public void topologicalSort()
{
int orig_nVerts = nVerts;
while(nVerts>0)
{
int currentVertex = noSuccessors();
if(currentVertex == -1)
{
System.out.println("Error:Graph has cycles");
return ;
}
//先找到拓扑排序的最后的节点
sortedArray[nVerts-1] = vertexList[currentVertex].label;
deleteVertex(currentVertex);
}
System.out.print("Topologically sorted order:");
for(int j=0;j<orig_nVerts;j++)
System.out.println(sortedArray[j]);
System.out.println();
}
//找到一个节点没有后继
public int noSuccessors()
{
boolean isEdge;
for(int row=0;row<nVerts;row++)
{
isEdge = false;
for(int col=0;col<nVerts;col++)
{
if(adjMat[row][col]>0)
{
isEdge = true;
break;
}
}
if(!isEdge)
return row;
}
return -1;
}
public void deleteVertex(int delVert)
{
if(delVert != nVerts-1)
{
for(int j=delVert;j<nVerts-1;j++)
vertexList[j] = vertexList[j+1];
for(int row=delVert;row<nVerts-1;row++)
moveRowUp(row,nVerts);
for(int col=delVert;col<nVerts-1;col++)
moveColLeft(col,nVerts-1);
}
nVerts--;
}
private void moveRowUp(int row,int length)
{
for(int col=0;col<length;col++)
adjMat[row][col] = adjMat[row+1][col];
}
private void moveColLeft(int col,int length)
{
for(int row=0;row<length;row++)
adjMat[row][col] = adjMat[row][col+1];
}
}
public class MatrixDG_TOPO
{
public static void main(String[] args)
{
DGraph theGraph = new DGraph();
theGraph.addVertex('A'); // 0
theGraph.addVertex('B'); // 1
theGraph.addVertex('C'); // 2
theGraph.addVertex('D'); // 3
theGraph.addVertex('E'); // 4
theGraph.addVertex('F'); // 5
theGraph.addVertex('G'); // 6
theGraph.addVertex('H'); // 7
theGraph.addEdge(0, 3); // AD
theGraph.addEdge(0, 4); // AE
theGraph.addEdge(1, 4); // BE
theGraph.addEdge(2, 5); // CF
theGraph.addEdge(3, 6); // DG
theGraph.addEdge(4, 6); // EG
theGraph.addEdge(5, 7); // FH
theGraph.addEdge(6, 7); // GH
theGraph.topologicalSort(); // do the sort
}
}
邻接链表:
import java.util.ArrayList;
class Vertex
{
public char label;
public int index;//数组下标索引编号
public Edge firstEdge;
public int inDegree;//入度
public Vertex(char lab){
index = 0;
inDegree = 0;
label = lab;
firstEdge = null;
}
}
class Edge
{
public int dest;
public Edge nextEdge;
public Edge(int dest)
{
this.dest= dest;
nextEdge = null;
}
}
class DGraph
{
private final int MAX_VERTS = 20;
private int nVerts = 0;
private Vertex[] vertexList;
private ArrayList<Vertex> topoList;
public DGraph()
{
vertexList = new Vertex[MAX_VERTS];
topoList = new ArrayList<Vertex>();
}
public void addVertex(Vertex vertex)
{
vertex.index = nVerts;
vertexList[nVerts++] = vertex;
}
public void addEdge(int start,int end)
{
vertexList[end].inDegree++;
Edge endEdge = new Edge(end);
Edge currentEdge = vertexList[start].firstEdge;
if(currentEdge==null)
{
vertexList[start].firstEdge = endEdge;
}else
{
while(currentEdge.nextEdge!=null)
currentEdge = currentEdge.nextEdge;
currentEdge.nextEdge = endEdge;
}
}
public void topologicalSort()
{
for(int i=0;i<nVerts;i++)
{
Vertex vertex = noPrevious();
if(vertex == null)
{
System.out.println("Error:Graph has cycles");
return ;
}
topoList.add(vertex);
deleteVertex(vertex);
}
}
public Vertex noPrevious()
{
int i=0;
for( ;i<nVerts;i++)
{
if(vertexList[i] != null && vertexList[i].inDegree==0)
break;
}
if(i==nVerts)
return null;
else
return vertexList[i];
}
public void deleteVertex(Vertex vertex)
{
Edge currentEdge = vertex.firstEdge;
if(currentEdge == null)
return;
while(currentEdge != null){
vertexList[currentEdge.dest].inDegree--;
currentEdge = currentEdge.nextEdge;
}
/* //删除顶点数组中的一个顶点
for(int j=vertex.index;j<nVerts-1;j++){
vertexList[j] = vertexList[j+1];
vertexList[j].index = j;
}*/
vertexList[vertex.index] = null;
//nVerts--;
}
public void displayTopo()
{
System.out.println("topologicalSort:");
for(int i=0;i<topoList.size();i++)
System.out.print(topoList.get(i).label);
System.out.println("");
}
}
public class ListDG_TOPO
{
public static void main(String[] args)
{
DGraph theGraph = new DGraph();
theGraph.addVertex(new Vertex('A'));// 0
theGraph.addVertex(new Vertex('B'));// 1
theGraph.addVertex(new Vertex('C'));// 2
theGraph.addVertex(new Vertex('D'));// 3
theGraph.addVertex(new Vertex('E'));// 4
theGraph.addVertex(new Vertex('F'));// 5
theGraph.addVertex(new Vertex('G'));// 6
theGraph.addVertex(new Vertex('H'));// 7
theGraph.addEdge(0, 3);// AD
theGraph.addEdge(0, 4);// AE
theGraph.addEdge(1, 4);// BE
theGraph.addEdge(2, 5);// CF
theGraph.addEdge(3, 6);// DG
theGraph.addEdge(4, 6);// EG
theGraph.addEdge(5, 7);// FH
theGraph.addEdge(6, 7);// GH
theGraph.addEdge(2, 1);// CB
theGraph.addEdge(6, 5);// GF
theGraph.topologicalSort();
theGraph.displayTopo();
}
}


