李宏毅机器学习笔记09(Unsupervised Learning 01——Clustering and PCA)
无监督学习
1、无监督学习的概念
什么叫无监督学习(输入都是无label的数据,没有训练集之说)
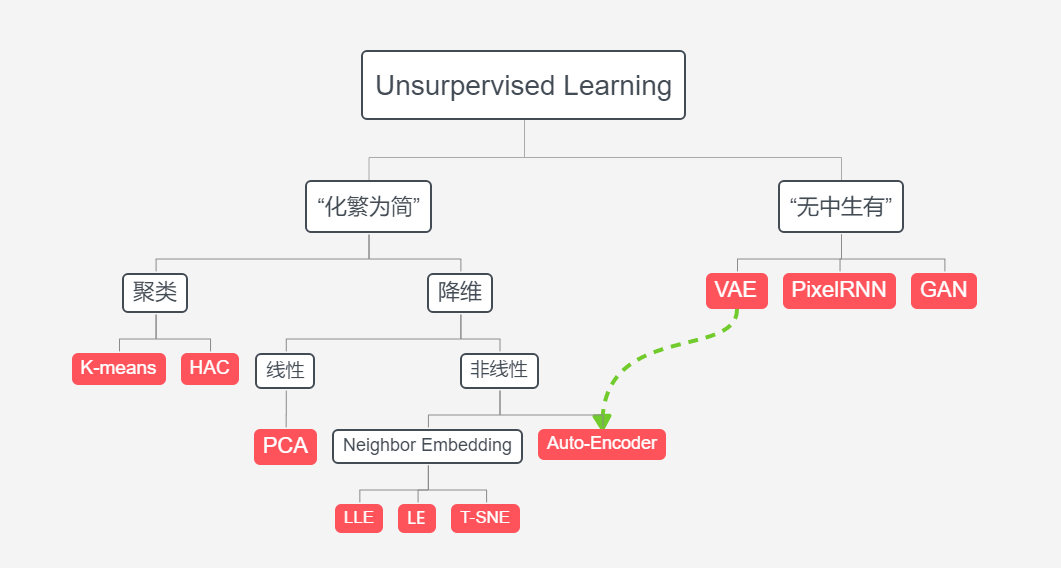
无监督学习的两大任务:“化繁为简”(聚类、降维)、“无中生有”
2、聚类Clustering(K-means、HAC)
3、降维Dimension Reduction(PCA)
1、无监督学习的概念
一、什么叫无监督学习
输入都是无label的数据,没有训练集之说,也就是只能从一些无label的数据中自己寻找规律
二、无监督学习的两大任务:“化繁为简”(聚类、降维)、“无中生有”
2、聚类Clustering(K-means、HAC)
一、K-means算法

kmeans算法又名k均值算法。其算法思想大致为:先从样本集中随机选取 k 个样本作为簇中心,并计算所有样本与这 k 个“簇中心”的距离,对于每一个样本,将其划分到与其距离最近的“簇中心”所在的簇中,对于新的簇计算各个簇的新的“簇中心”。
根据以上描述,我们大致可以猜测到实现kmeans算法的主要几点:
(1)簇个数 k 的选择
(2)初始化簇中心(可以从你的train data里面随机找K个x出来,就是你的k个center)
while(收敛——聚类结果不再变化)
{
(3)各个样本点到“簇中心”的距离
(4)根据新划分的簇,更新“簇中心”(求均值)
}
二、HAC算法
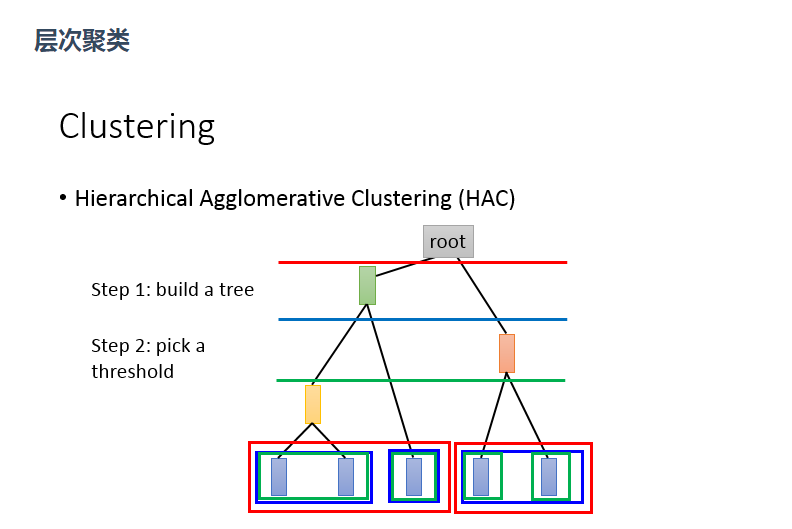
假设有5个样本,计算两两之间的相似度,将最相似的两个样本聚合在一起(比如第一个和第二个聚合成一个黄色类),再将剩下的4个聚合在一起,以此类推
3、降维Dimension Reduction(PCA)
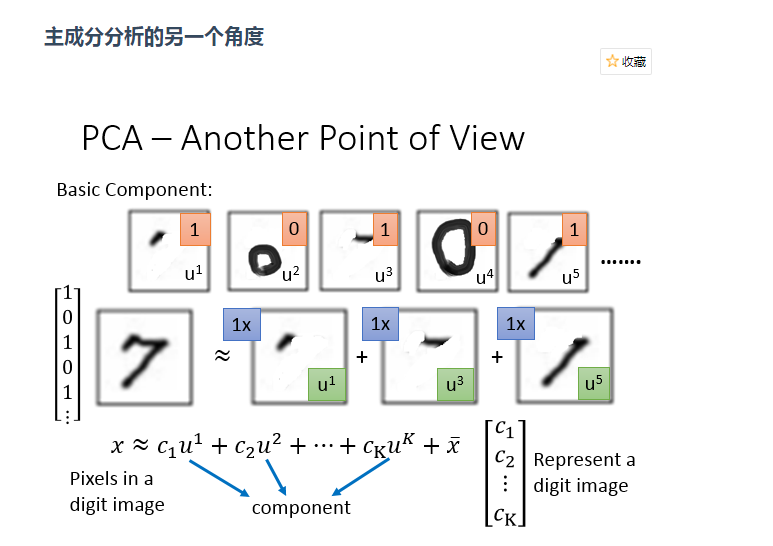
降维意思是说:原本高维的东西,其实是可以用低维去表示它,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。
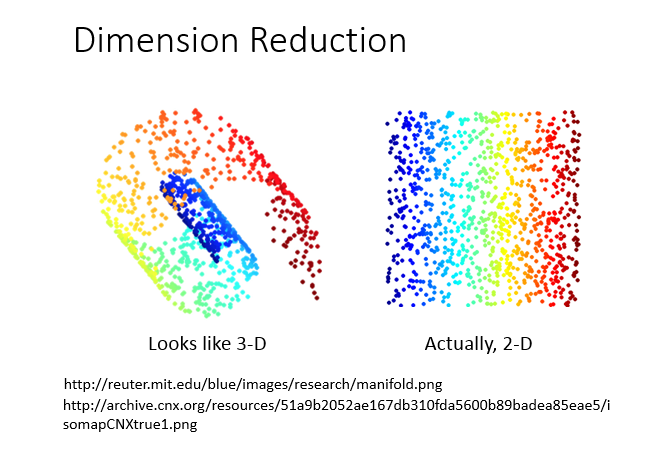
如果理想的话(如下图),我们可以直接抛弃下面的x1这个维度,但实际上我们不能直接拿掉某一个维度,
也就是说我们的数据跟每一个维度都有关系,这就需要主成分分析(PCA)

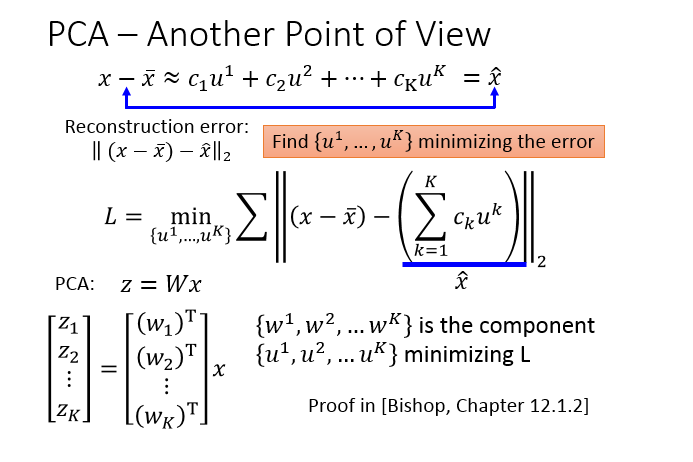
PCA实现
PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值分解去实现的。
(1)用特征值分解
现在举一个从二维数据降到一维的情况,
PCA做的事情就是:这个function(Z=Wx)是一个很简单的linear function,W就是我们要找的“一维”这个维度,Z是input x 从二维降到一维后的度量表示,
现在要做的事情就是:根据一大堆的x,我们要把w找出来!

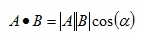
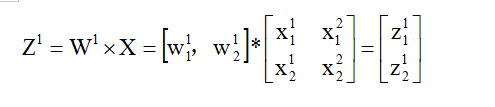
实际上w1就是一个row,假设w1的长度为1,那么对于一个数据来说,w1与x1的内积就等于x1在w1上的投影长度z1,那把所有x都输入就得到一堆的z1(如上面右图)。
那么我们寻找w1的规则就是,令z1的方差最大(数据识别度最大)
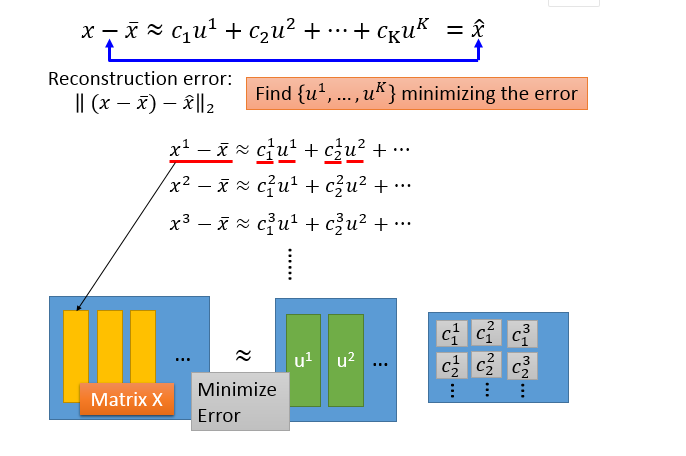
这就需要矩阵论的知识,把多个w放在一个矩阵里面计算,但要注意的是此时就需要w两两正交,也就是大W是一个正交矩阵
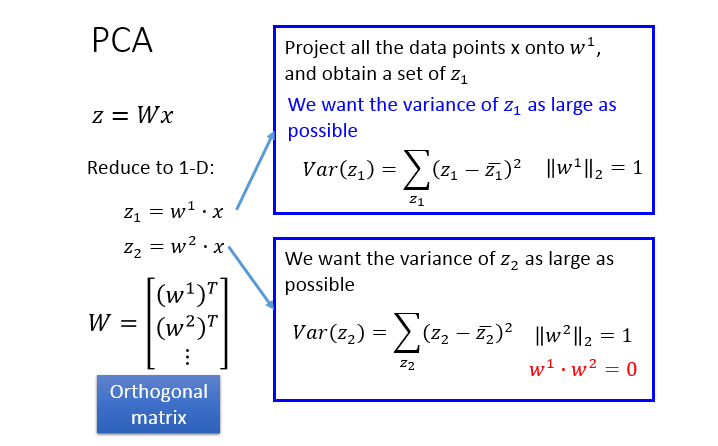
开始计算:
1、把方差式子展开,转化成协方差(具体转化过程不描述了)
2、结论:我们要找的w1就是协方差矩阵S的最大特征值所对应的特征向量,w2就是协方差矩阵S的第二大特征值所对应的特征向量,以此类推



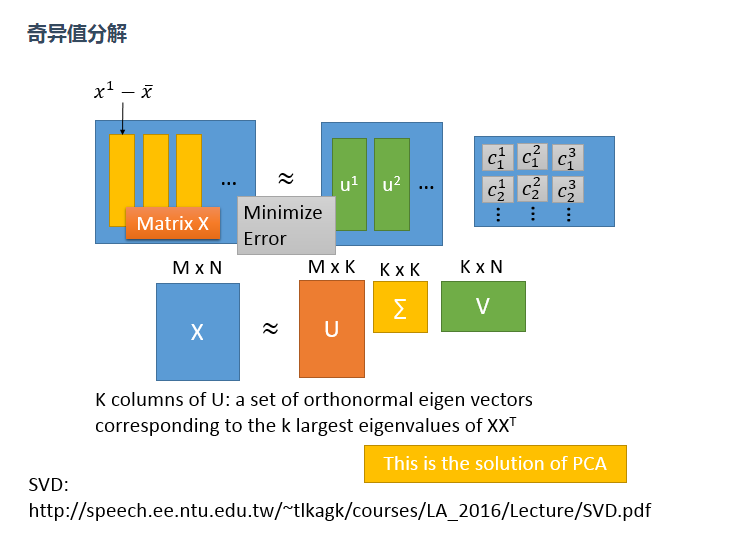
(2)用奇异值分解(SVD)
特征值分解是一个提取矩阵特征很不错的方法,但是它只是对方阵而言的,在现实的世界中,我们看到的大部分矩阵都不是方阵。奇异值分解是一个能适用于任意的矩阵的一种分解的方法。