李宏毅机器学习笔记08(Semi-Supervised)
半监督学习
1、什么是Semi-Supervised
2、Semi-Surpervised在生成模型中如何实现的(EM算法)
3、Semi-Surpervised基于Low-density Separation(低密度分离)假设是如何实现的
1)Self-training方法+Entropy-based Regularization
2)SVM
4、Semi-Surpervised基于Smoothness Assumption(平滑)假设是如何实现的
1)Cluster and then Label
2)Graph-based Approach(KNN算法)
1、什么是Semi-Supervised

举个栗子:现在我们要做一个猫狗分类,
- 如果只考虑labeled data,我们分类的分界线会画在中间;
- 但如果把unlabeled data 也考虑进去,我们可能会根据unlabeled data 的分布,分界线画成图中的斜线;
- semi-supervised learning使用unlabel的方式往往伴随着一些假设,学习有没有用,取决于你这个假设合不合理。(比如灰色的点也可能是个狗不过背景跟猫照片比较像)


2、Semi-Surpervised在生成模型中如何实现的(EM算法)
- 回顾有监督学习中的生成模型,由于data都是有label的,P(Ci)是已知的,P(x|Ci)是通过我们基于高斯分布的假设用最大似然估计出来的;
- 现在半监督学习中的生成模型,data的一部分是unlabel的,P(Ci)是不确定的(隐变量),P(x|Ci)的假设模型也不能套用原来的u等参数,这时候需要用EM算法


EM算法(Expectation-Maximization algorithm,又译为期望最大化算法)
- EM算法适用于带有无法观测的隐变量的概率模型估计
- 第一步,用labeled data算出来的高斯模型参数代入公式去求出unlabeled data的P(C1|Xu);
- 第二步,用极大似然估计更新P(Ci)以及高斯模型参数,求出P(x|Ci),进一步求出新的(Ci|Xu),重复这两步直到收敛(似然概率最大)
(至于为什么更新参数是要加入P(Ci|Xu)这一项,是因为EM算法的思想是把不确定的data用一个概率来表示label,而每一笔不确定的data都有可能来自C1和C2,看右下图)


3、Semi-Surpervised基于Low-density Separation(低密度分离)假设是如何实现的
- 生成模型的假设中,假设不确定的data的label是一个概率值
- 低密度分离的假设是,不确定的data的label要不是1,要不是0(“非黑即白”)。低密度的意思是,两个Class的分界处是低密度的(分得比较开的)

1)Self-training+Entropy-based Regularization
- 利用labeled的数据训练(逻辑回归,神经网络,决策树等)出模型
;
- 将一组unlabeled的数据代入,得到新的标签,称为Pseudo-label伪标签;
- 将刚才得到新标签数据的一部分和labeled数据结合到一起,得到训练新的模型,重复以上步骤;
注:在做regression时是不能用这一招的,主要因为把unlabeled data加入到训练数据中,f*并不会受影响

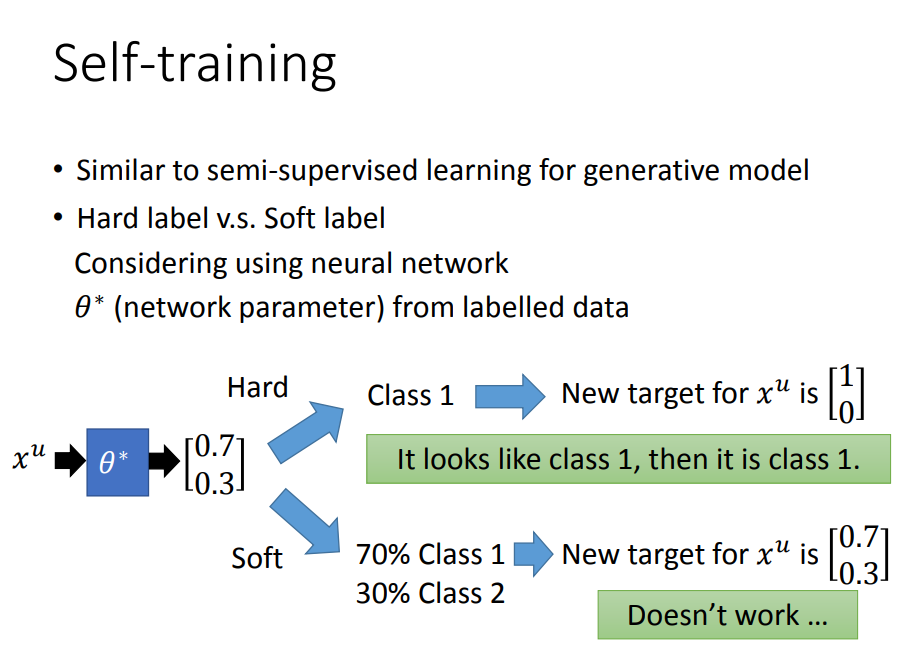
加上Entropy-based Regularization
接着Self-Learning做进一步改进:
- 基于熵的正则假设:假设输出是一个分布(类似于生成模型的概率),那么根据“低密度分离”原则,我们希望每输出一个值,它的分布都是很集中的(“非黑即白”)
- 用熵可以描述集中不集中这件事情,在Loss函数中加入unlabeled data的熵(相当于上面方法基础上加上正则项),我们希望这个熵越小越好

2)SVM
4、Semi-Surpervised基于Smoothness Assumption(平滑性)假设是如何实现的
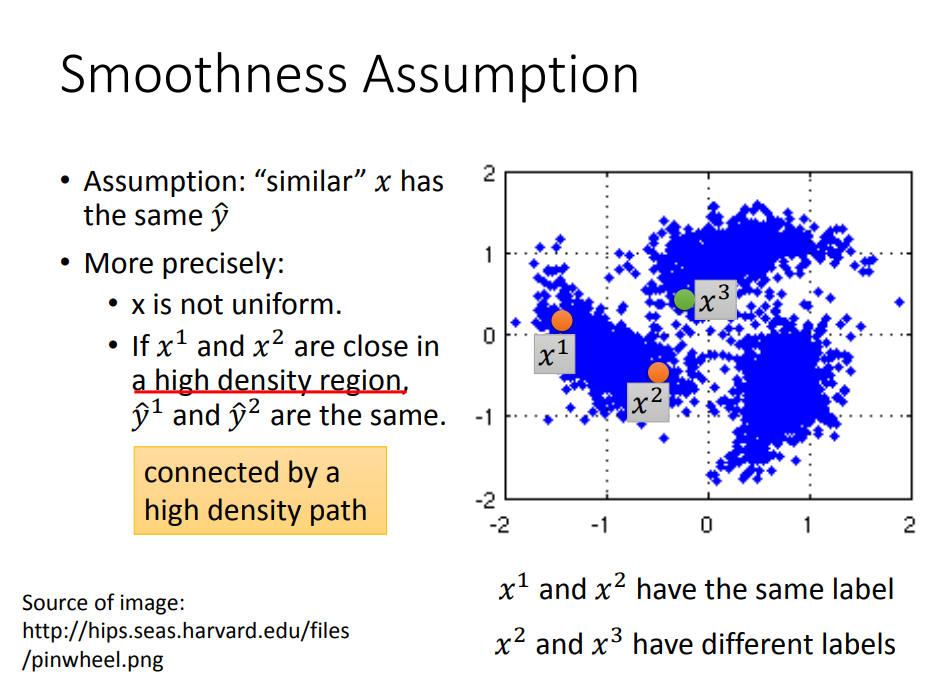
平滑性假设 :
- x的分布是不均匀的,在有的地方是稀疏的,在有的地方是密集的
- 如果在高密度区域比较相近,那么这两个数据具有相同的标签。
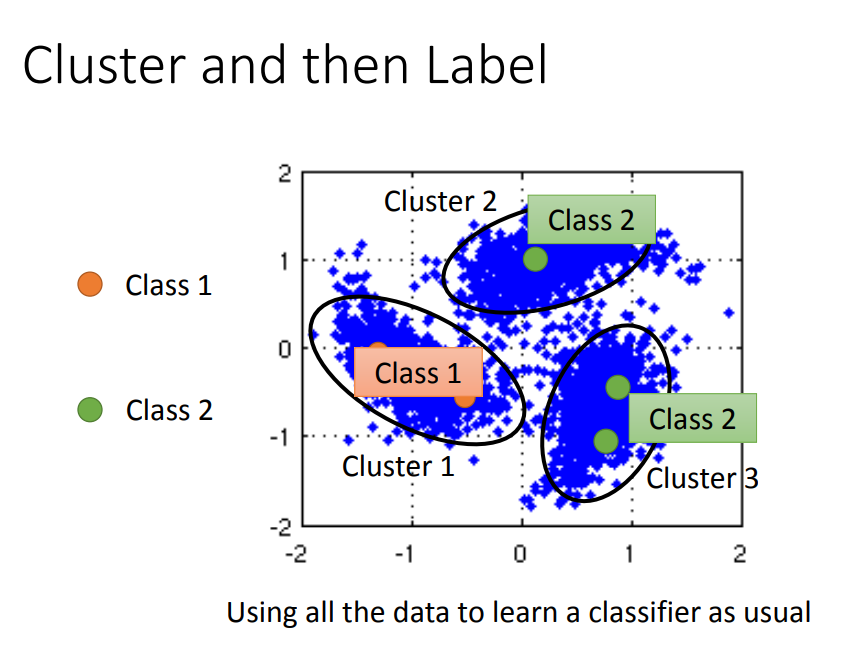
1)Cluster and then Label(先聚类后标注)
2)Graph-based Approach(KNN算法)
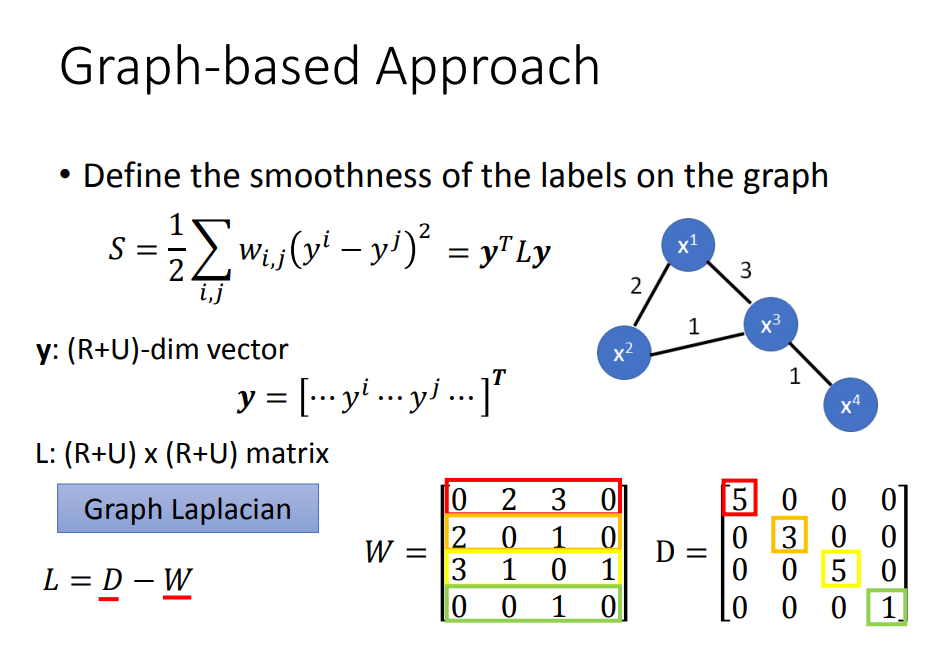
目标:我们希望利用基于图的方法,建立起下图的模型
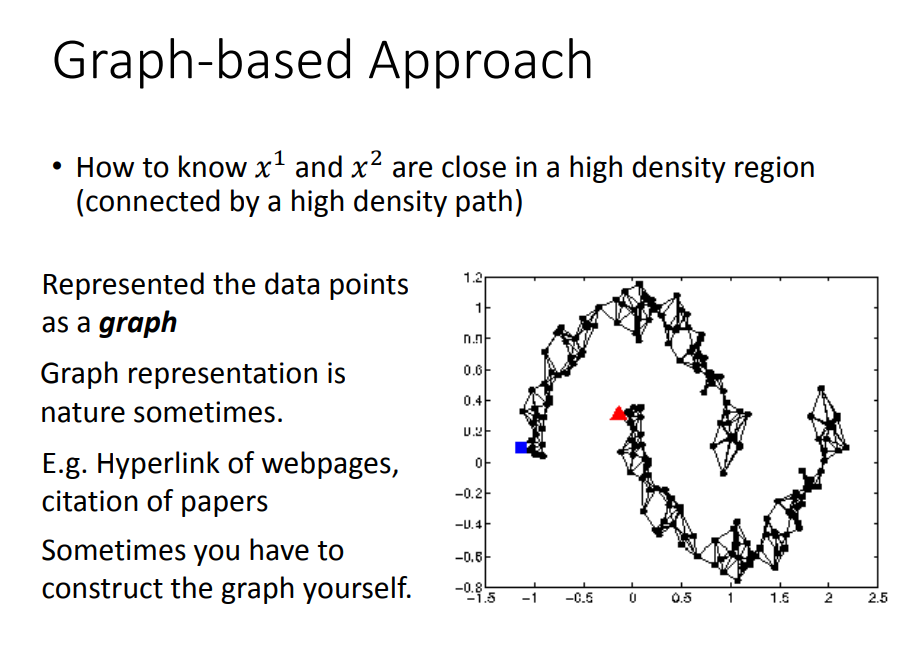
方法:
- 定义相似度,可以根据相似度定权重(加exp)
-
添加边界: 用KNN(根据“距离”找出K个最近的邻居)或者e-Neighborhood(超过阈值e才建立边)
要求有足够的数据才work

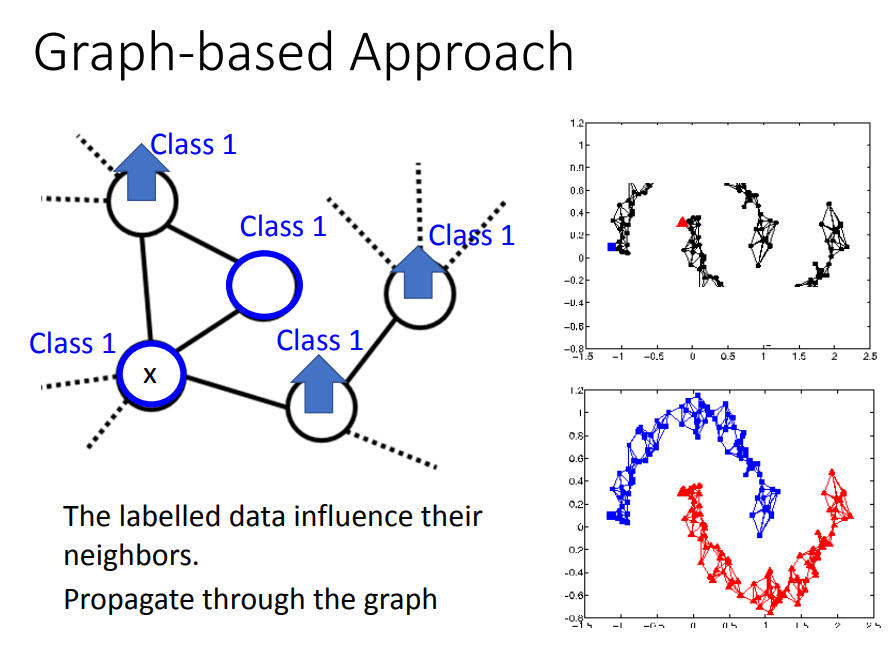
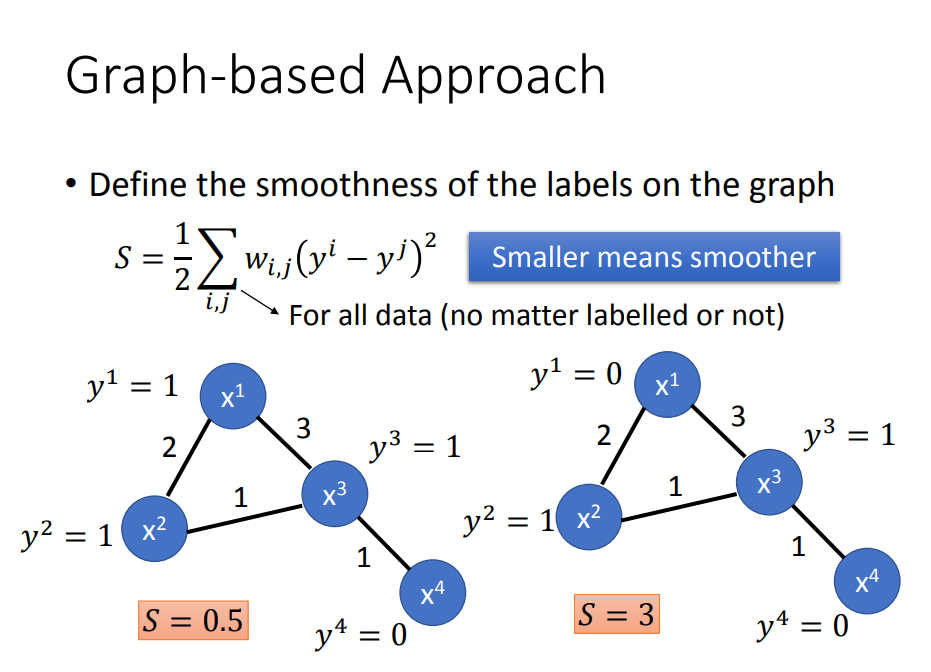
- 前面说半监督学习有没有用,取决于你这个假设合不合理。那么我们用以下的S值来评价假设有多合理