李宏毅机器学习笔记01(regression)
Regression
1、首先,什么是regression(回归)
2、然后,实现回归的步骤(机器学习的步骤)
step1、model(确定一个模型)——线性模型
step2、goodness of function(确定评价函数)——损失函数
step3、best function(找出最好的一个函数)——梯度下降法
3、进一步,如何做得更好(优化step1)
方法1、select another model(选择另一个模型)
方法2、consider the hidden factors(考虑其他隐藏因素)
4、再进一步,防止过拟合(优化step2)
方法:正则化
5、最后,总结
1、首先,什么是regression(回归)
Regression 就是找到一个函数 function,通过输入特征 x ,输出一个数值 Scalar 。

- 股市预测(Stock market forecast)
输入:过去10年股票的变动、新闻咨询、公司并购咨询等
输出:预测股市明天的平均值
- 自动驾驶(Self-driving Car)
输入:无人车上的各个sensor的数据,例如路况、测出的车距等
输出:方向盘的角度
- 商品推荐(Recommendation)
输入:商品A的特性,商品B的特性
输出:购买商品B的可能性
2、然后,实现回归的步骤(机器学习的步骤)
举个栗子:我们要预测Pokemon精灵攻击力。
输入:进化前的CP值、物种(Bulbasaur)、血量(HP)、重量(Weight)、高度(Height)
输出:进化后的CP值

step1、model(确定一个模型)——线性模型
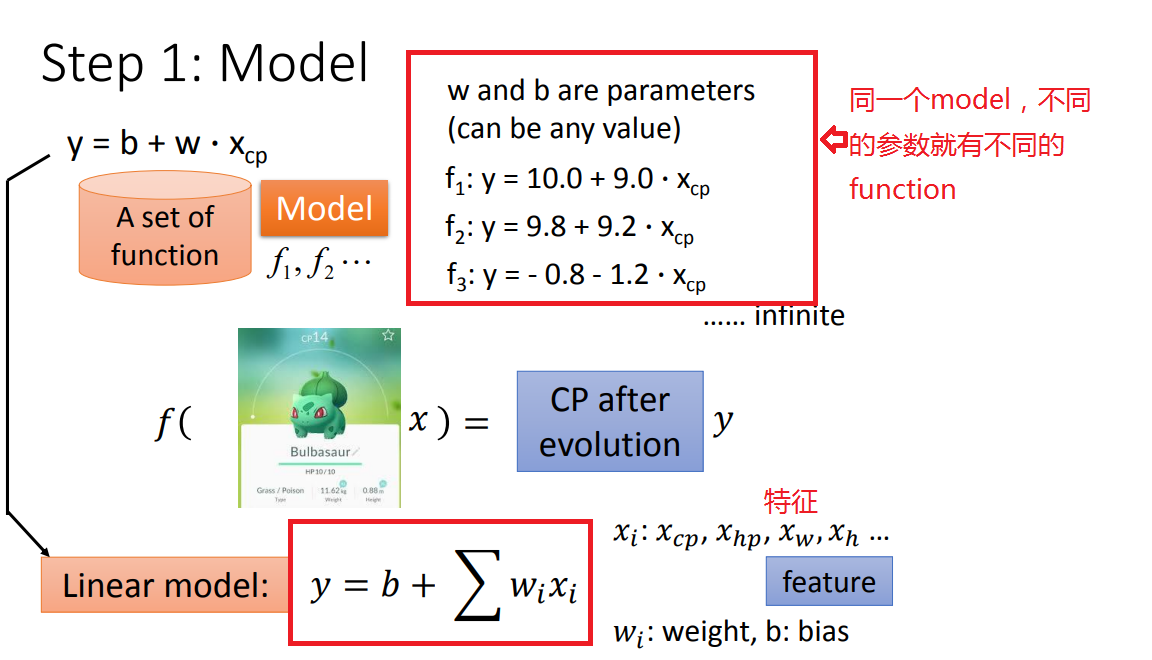
先从简单的单个特征(Xcp)开始(后面改进再考虑多个特征)。
step2、goodness of function(确定评价函数)——损失函数
1、确定好model以后,就开始训练数据
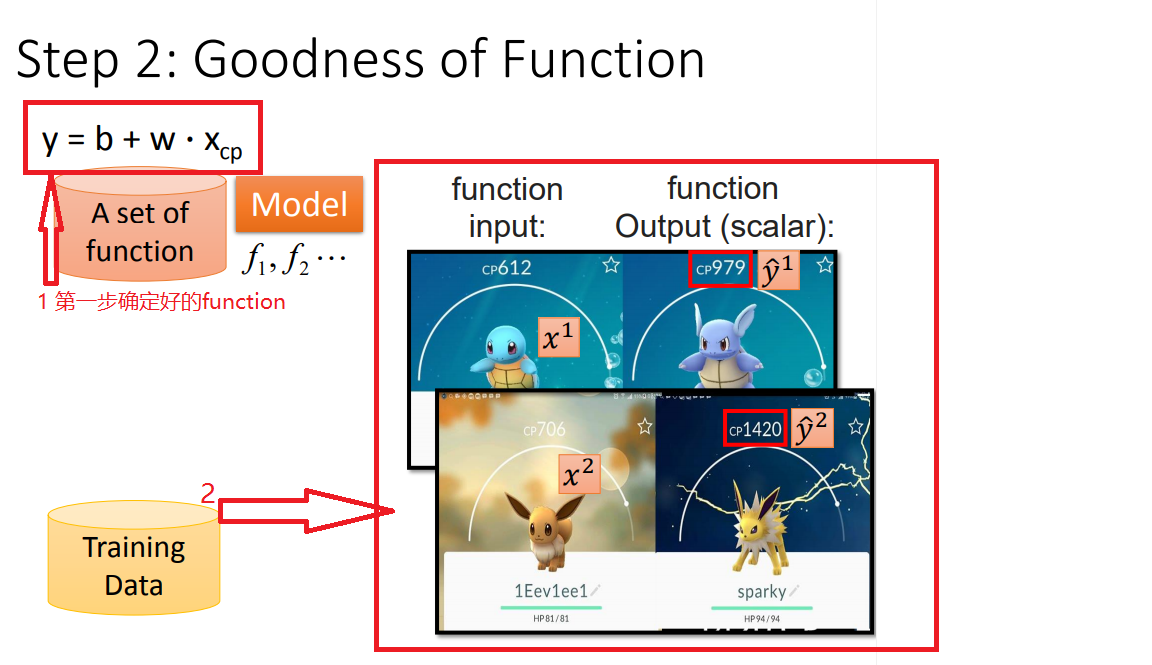
以此类推,训练10个数据:

2、确定损失函数
有了这些真实的数据,那我们怎么衡量模型的好坏呢?从数学的角度来讲,我们使用距离。求实际进化后的CP值与模型预测的CP值差,来判定模型的好坏。
也就是使用 损失函数(Loss function) 来衡量模型的好坏,和越小模型越好。如下图所示:

step3、best function(找出最好的一个函数)——梯度下降法
1、找到一个best function(说白了是找最佳的参数),也就是使损失函数最小时候的参数

2、用梯度下降法,求最佳参数
1)梯度是什么?梯度下降又是什么?
梯度:
- 在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
- 在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
梯度下降:“下山最快路径”的一种算法
2)先考虑简单的一个参数w
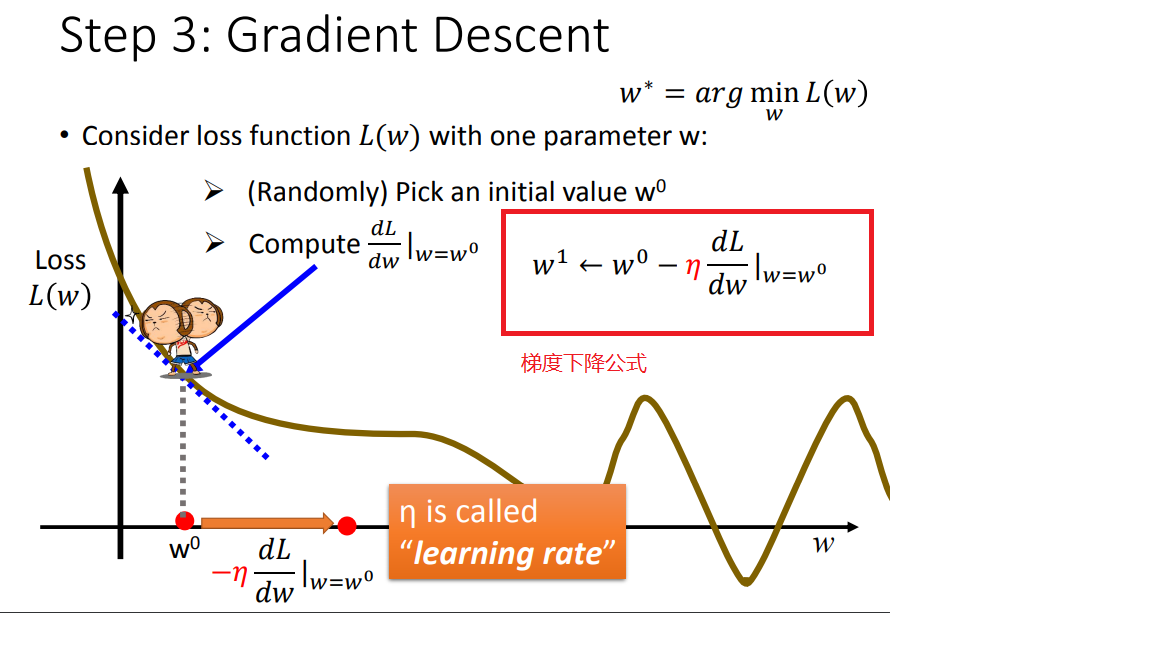
首先在这里引入一个概念 学习率 :移动的步长,如图7中 η (eta)
步骤1:随机选取一个 w0 。
步骤2:计算微分,也就是当前的斜率,根据斜率来判定移动的方向。
大于0向右移动(增加w)
小于0向左移动(减少w)
步骤3:根据学习率移动。
重复步骤2和步骤3,直到找到最低点。
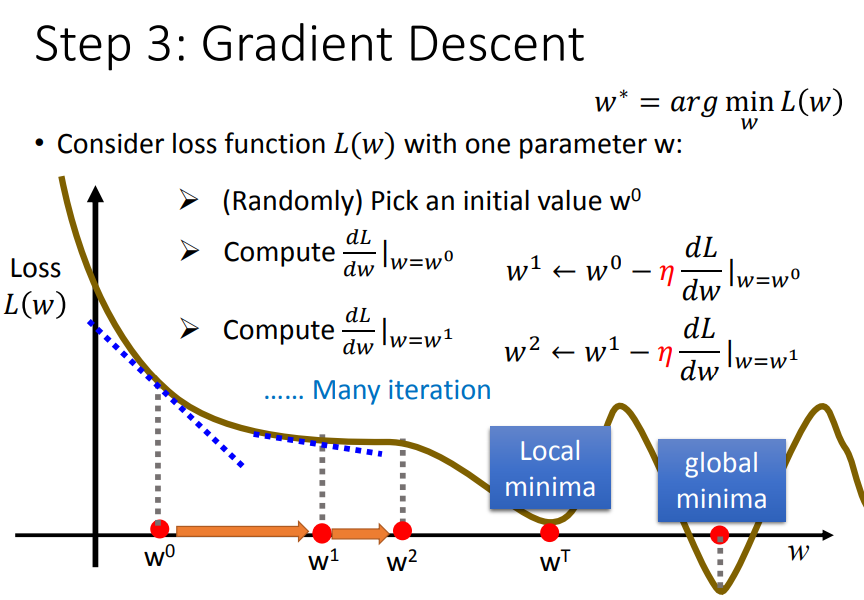
3)再考虑两个参数(w、b)

3、梯度下降法的效果
颜色约深的区域代表的损失函数越小

4、梯度下降的缺点
总结一下梯度下降法:我们要解决使L(x)最小时参数的最佳值,梯度下降法是每次update参数值,直到损失函数最小。

但是梯度下降法会出现问题呢?

step4、回归结果分析
经过上述三个步骤后,我们就得到了训练后的“最佳参数w,b”,那么它在测试集的performance怎么样呢?下面一起来看看吧
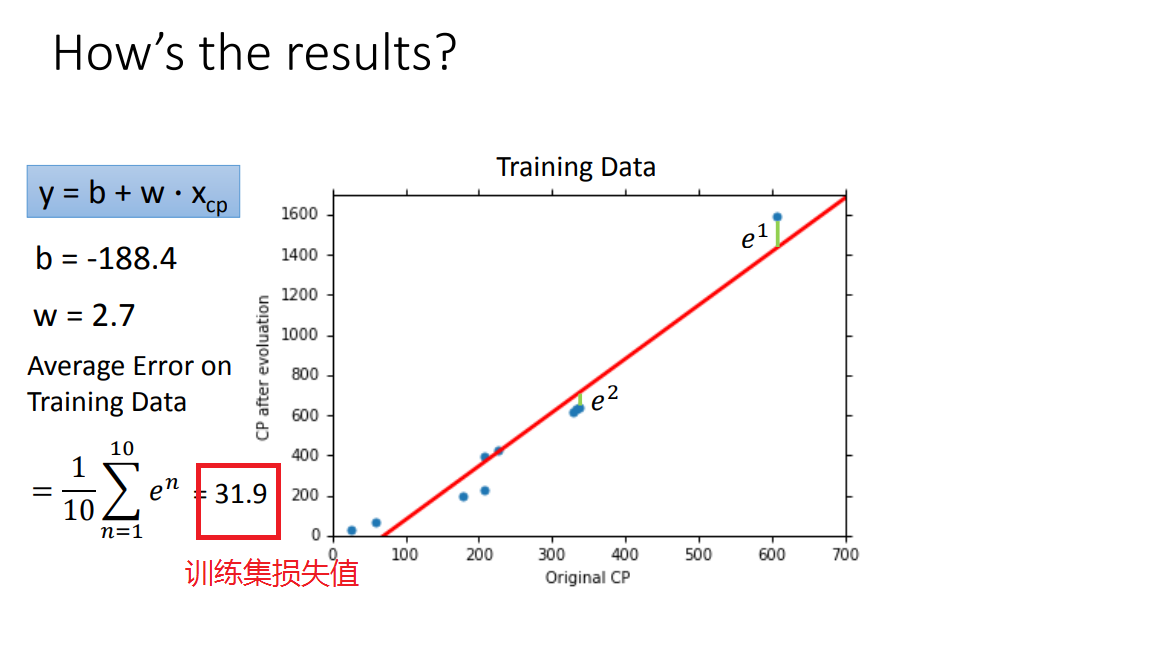

如何优化呢?继续看吧
3、进一步,如何做得更好(优化step1欠拟合)
方法1、select another model(选择另一个模型)
1、model改用不同函数的performance:
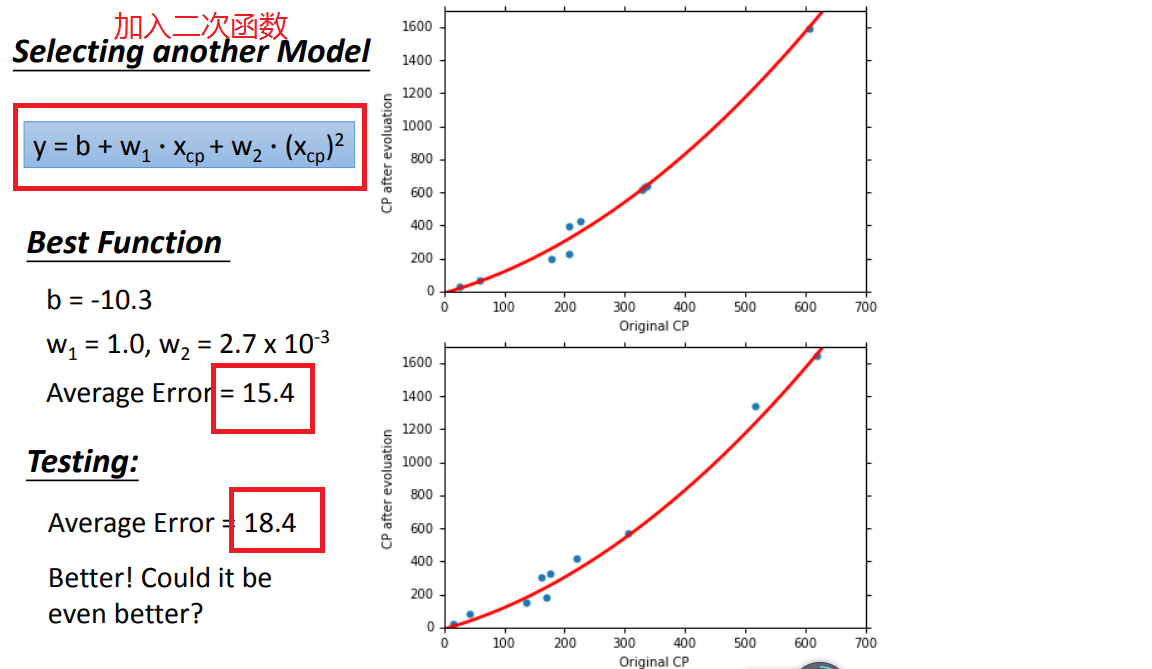


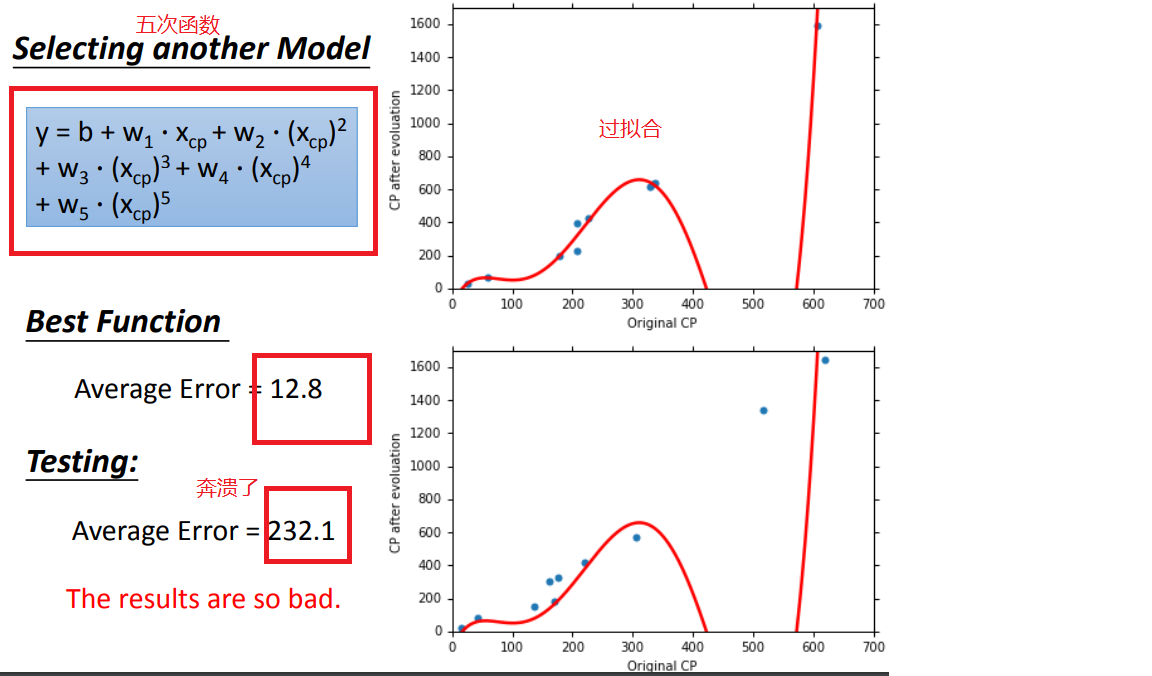
2、如何选择model呢
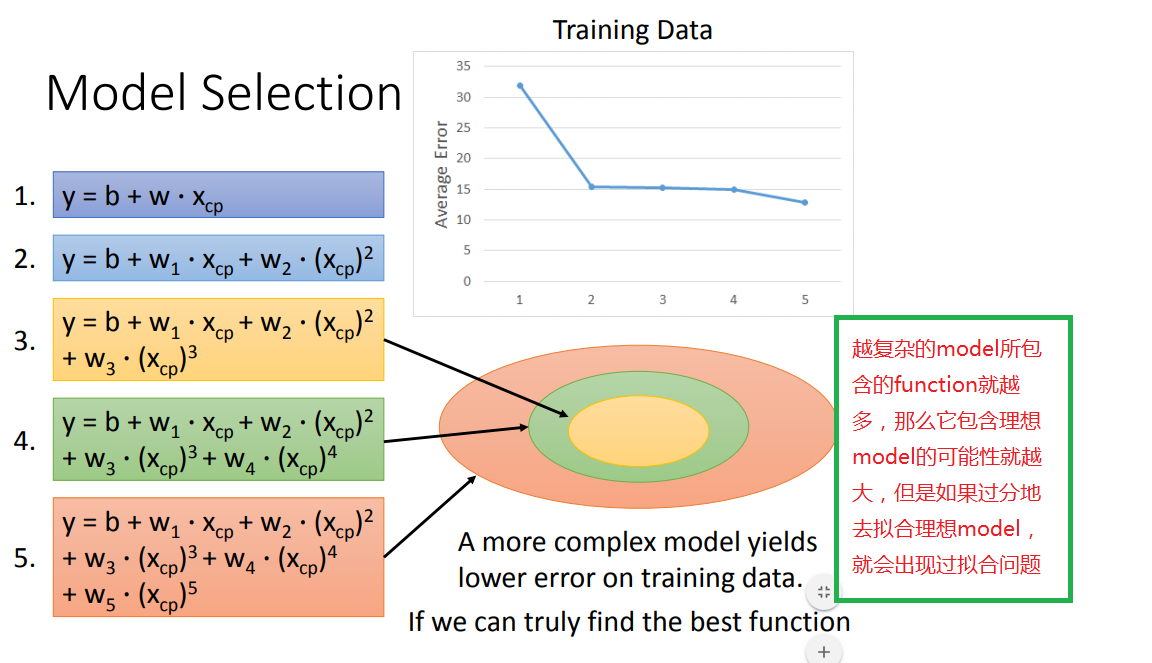

超过三次函数以上的model都出现了过拟合问题,因此要找到一个suitable model(这里是第三个)
方法2、consider the hidden factors(考虑其他隐藏因素)
1、再考虑另外一个因素(精灵的种类)
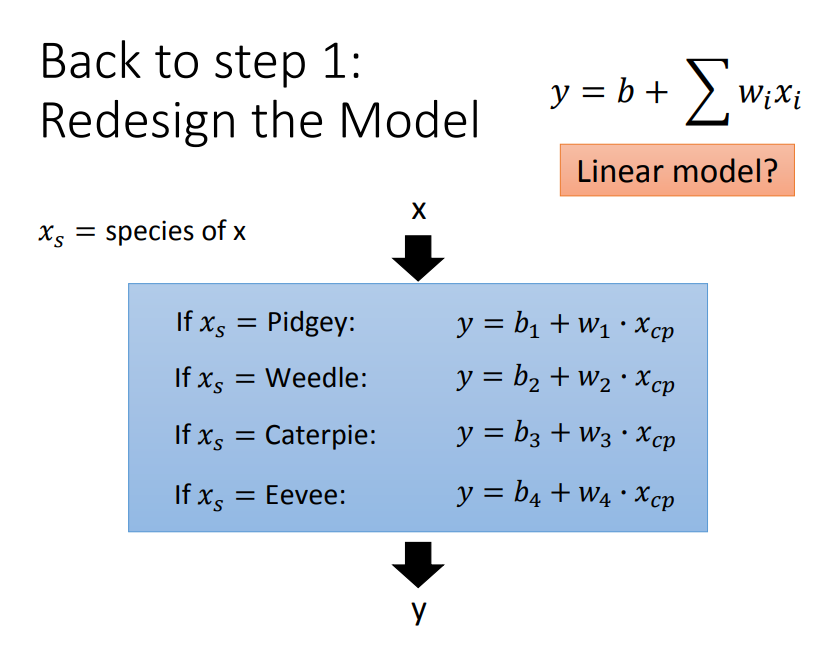

performance:
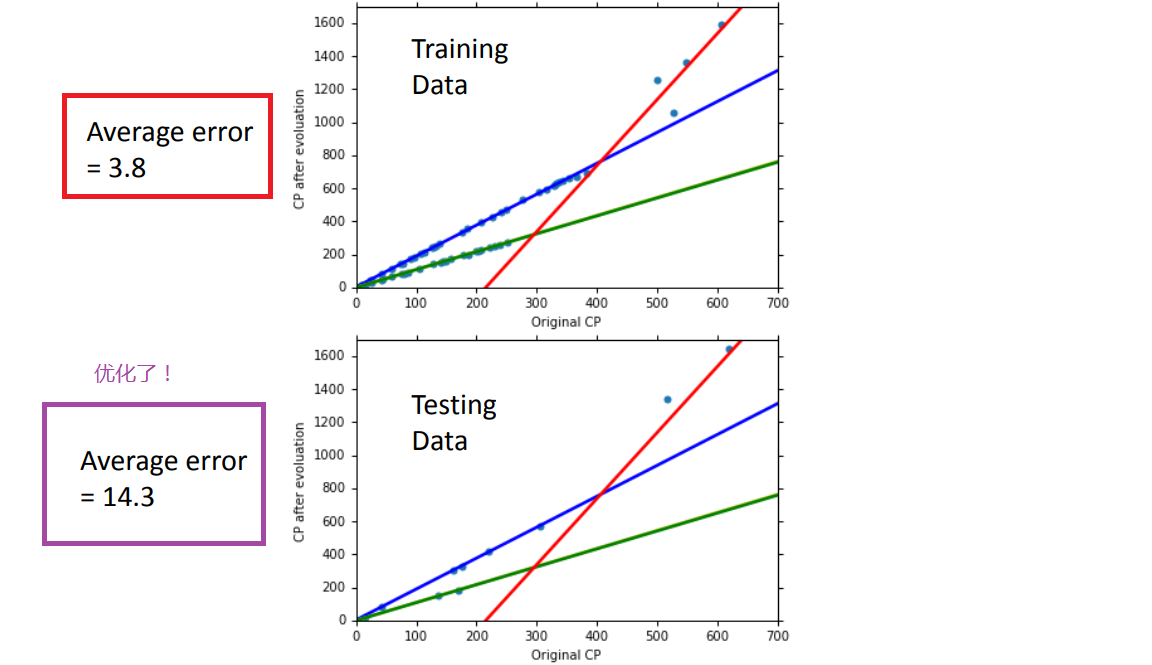
2、把更多的因素都考虑
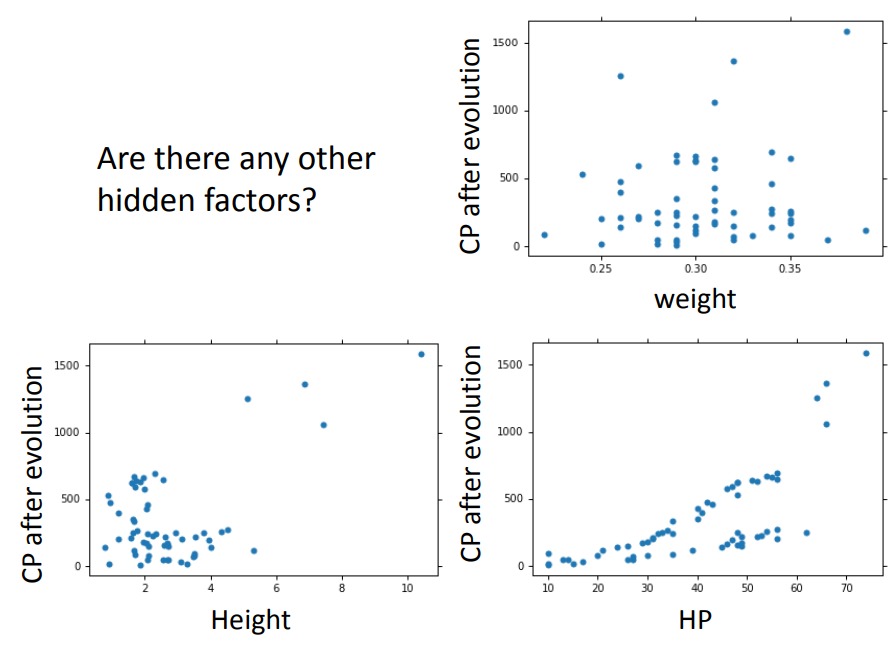

考虑更多的因素反而出现了过拟合的问题,说明有些因素跟本次实验的CP值预测没有关系!
过拟合这么讨厌,到底如何减少过拟合问题呢?往下看!
4、再进一步,防止过拟合(优化step2)
方法:正则化
1、比如先考虑一个参数w,正则化就是在损失函数上加上一个与w(斜率)相关的值,那么要是loss function越小的话,w也会越小,w越小就使function更加平滑(function没那么大跳跃)

2、正则化的缺点
正则化虽然能够减少过拟合的现象,但是因为加在损失函数后面的值是平白无故加上去的,所以正则化过度的话会导致bias偏差增大
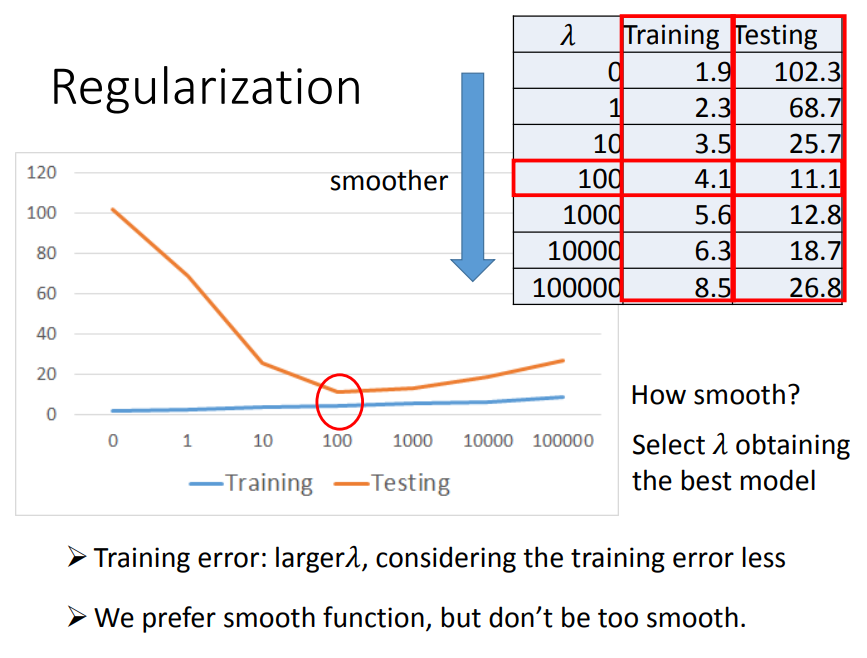
5、最后,总结




