计算机组成原理
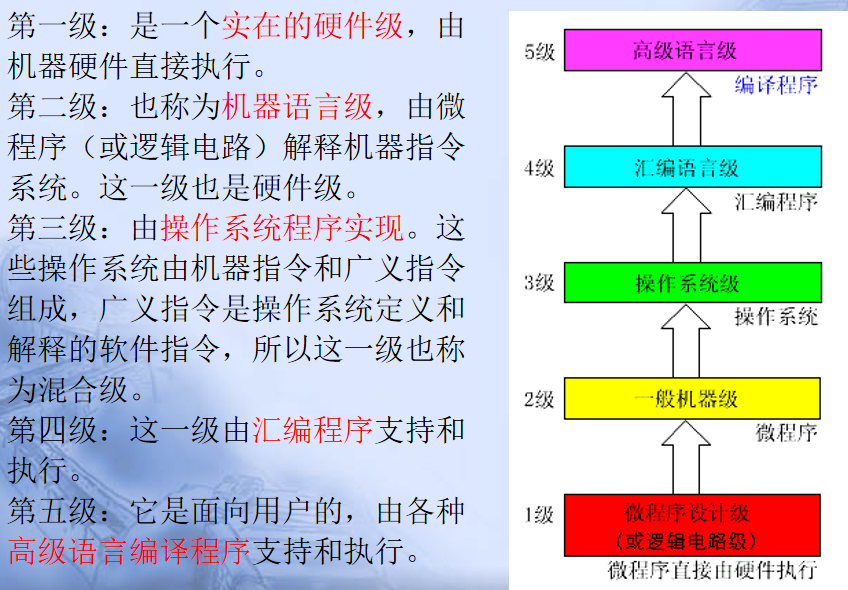
第一章:计算机系统概论
1.1 计算机分类:
按信息的形式及处理方式分:模拟电子计算机和数字电子计算机
按用途分:通用计算机和专用计算机
按规模分:超级计算机、大型机、服务器、工作站 、微型机、单片机等
1.2计算机发展简史:
1.五代变化:电子管计算机、晶体管计算机、中小规模集成电路计算机(小型计算机)、大规模和超大规模集成计算机(微型计算机)、巨大规模集成电路计算机(单片机)
2.半导体存储器发展:
仙童半导体公司生产了第一个较大容量半导体存储器,后面每代的容量都增大四倍
3.微处理器的发展
4.计算机的性能指标:
总线宽度:一般指CPU中运算器与存储器之间进行互连的内部总线二进制位数。
存储器带宽:存储器的速度指标,单位时间内从存储器读出的二进制数信息量,一般用字节数/秒表示。

1.3计算机的硬件
1.冯·诺依曼计算机—存储程序概念

2. 数字计算机的硬件组成:
中央处理器(CPU) 主存储器 总线 适配器 外围设备
指令:![]()
总线的分类:根据总线上传送的信息可以分为数据总线、地址总线、控制总线
1.4计算机系统的层次结构
1.多级计算机系统
第二章:运算方法和运算器
2.1数据与文字的表示方法
一、数据格式
1.定点表示法
机器中所有数据的小数点位置固定,且位置是隐含的,不需要占一个位。
把小数点固定在有效数位的最前面或末尾,故,形成了两类定点数:定点小数(纯小数)、定点整数(纯整数)。

若x表示的是定点小数(纯小数),则小数点位于x0和x1之间; 若x表示的是定点整数(纯整数),则小数点位于xn之后。
2.浮点表示法

(1)浮点格式:
格式1:
由阶码(指数)、尾数及其符号位组成。

格式2:
按照 IEEE754 的标准,32位浮点数标准格式为 :

S:浮点数的符号位,占1 位,常用0表示正数,1表示负数。
M:尾数的数值部分,占23位,用小数表示,小数点放在尾数域的最前面。
E:阶码,8 位,阶符用该字段的最高位表示。
例子: 二进制数 x=1011.0110=0.10110110×24
用格式1表示x: 设m=6,n=8,符号位“0”表示正,“1”表示负

用格式2表示:

(2)浮点数的规格化表示:
1.一般意义下的规格化:

2.IEEE754标准中的规格化浮点表示

例子:

二、机器码的表示
1.原码表示法:
(1)定点整数:
例如,x=+1001,则[x]原=01001 ,x=-1001,则[x]原=11001
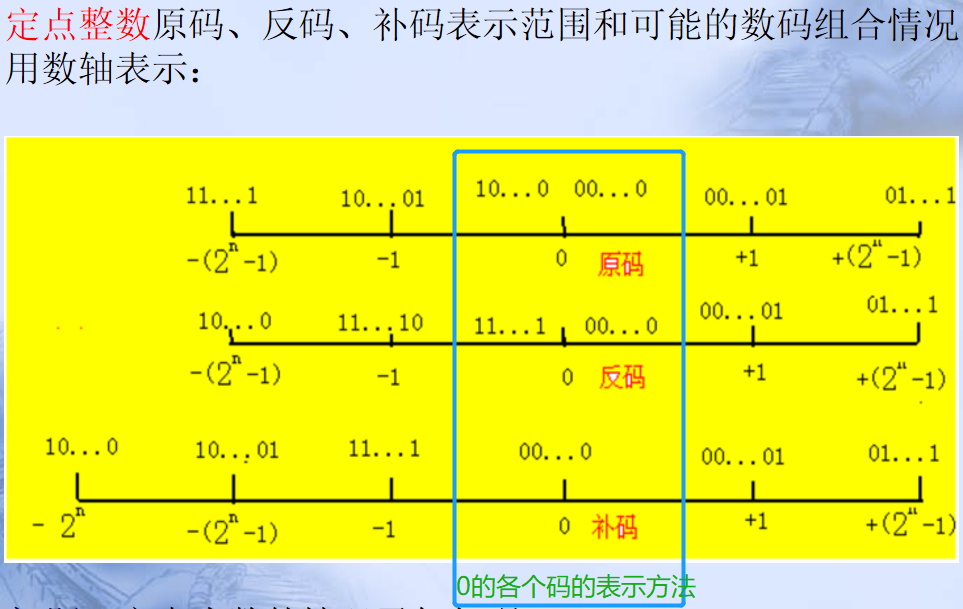
(2)定点小数
2.补码表示法
(1)定点小数的补码
例如,x=+0.1001,则[x]补=0.1001 x=-0.1001,则[x]补=1.0111
(2)定点整数的补码
若定点整数的补码形式为XnXn-1Xn-2…X0,则补码表示的范围是:
正数: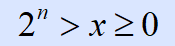
负数: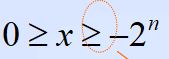
3.反码表示法
(1)定点小数的反码
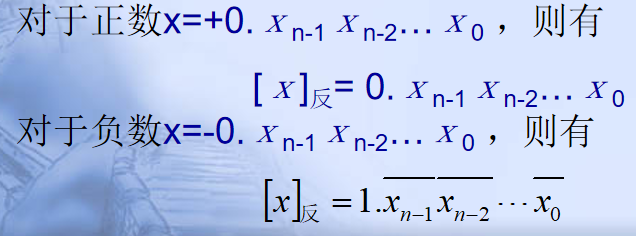
(2)定点整数的反码
4.移码的表示法
移码通常用于表示浮点数的阶码,因此需掌握定点整数的移码表示方法
移码就是将补码的符号位取反就好:

重点:机器码的规格化形式的相关规定(熟记)

重点例题:1.求规格化范围

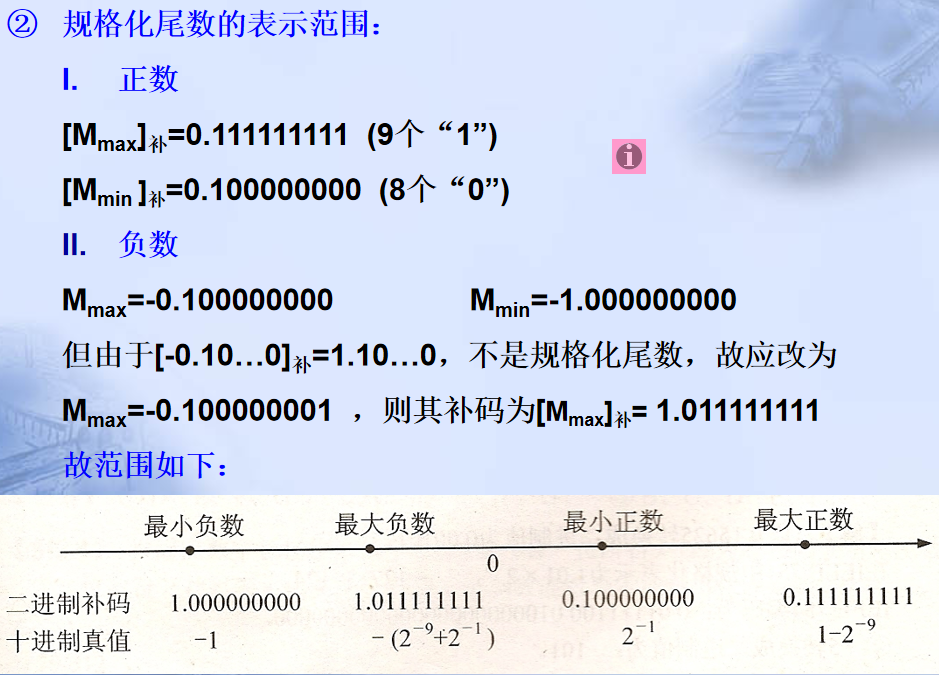

2.求754规格化范围

三、字符与字符串的表示方法
1.字符的表示方法:ASCII码,7位
2.字符串的存放:向量法(连续存放)、串表法(非连续存放)
四、汉字的表示方法
1.汉字的输入编码:数字编码(常用国标区位码)、拼音码、字形编码
2.汉字内码:占两个字节,最高位都为1
3.汉字字模码:只能用来构成汉字库,而不能用于机内存储,是汉字的输出形式。
2.2定点加法、减法运算
一、补码加法:
①符号位要作为数的一部分一起参加运算;②要在模2n+1 (或模2)的意义下相加,即符号位产生的进位要丢掉。
二、补码减法:
公式:[x-y]补= [x]补+[-y]补
由[y]补 求[-y]补 的法则: 各位都取反(包括符号位),然后末位+1
三、溢出概念与检测方法:
溢出:在定点整数机器中,数的表示范围为|x|<(2n-1)在运算过程中若出现大于(2n-1)的现象,则称为“溢出”。在定点机中,正常情况下溢出是不允许的。
检测方法:1.双符号位法:“01”表示上溢, “10”表示下溢。最高符号位始终表示结果的正确符号。
2.单符号位法:溢出检测逻辑表达式为V=Cf⊕Co,其中Cf为符号位产生的进位,Co为最高有效位产生的进位, V=1表示发生溢出。
四、定点加减运算的逻辑实现:
1.一位全加器估算时间延迟:
考虑溢出检测,那么n位串行进位加/减法器的延迟时间ta为:ta=n·2T+9T=(2n+9)T
当不考虑溢出检测时,有:ta=(n-1)·2T+9T
2.3定点乘法运算
一、原码乘法
符号位单独计算。
(1)串行实现:原码一位乘法算法

(2)原码并行乘法:
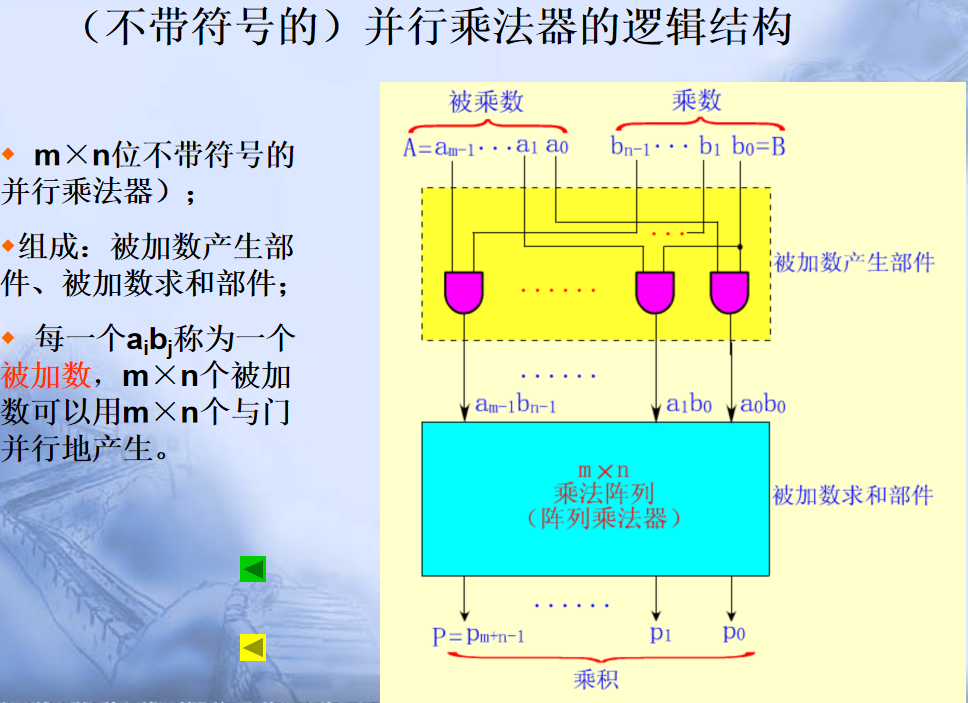
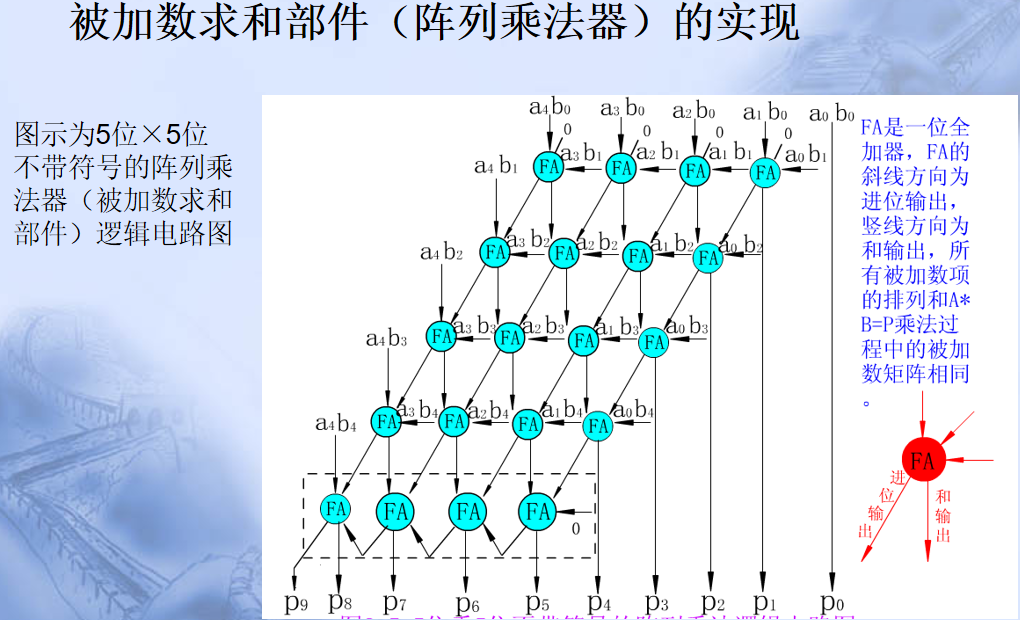
二、补码乘法
(1)间接补码并行乘法
1.原理: 特别需注意:负数的“原码→补码”和“补码→原码”的过程相同:数值位按位取反末位加1。

2.逻辑框图:
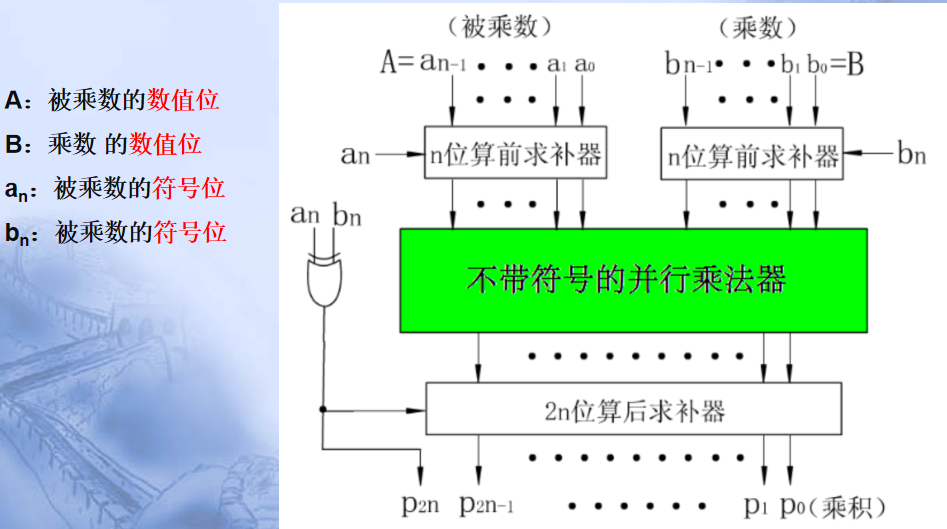
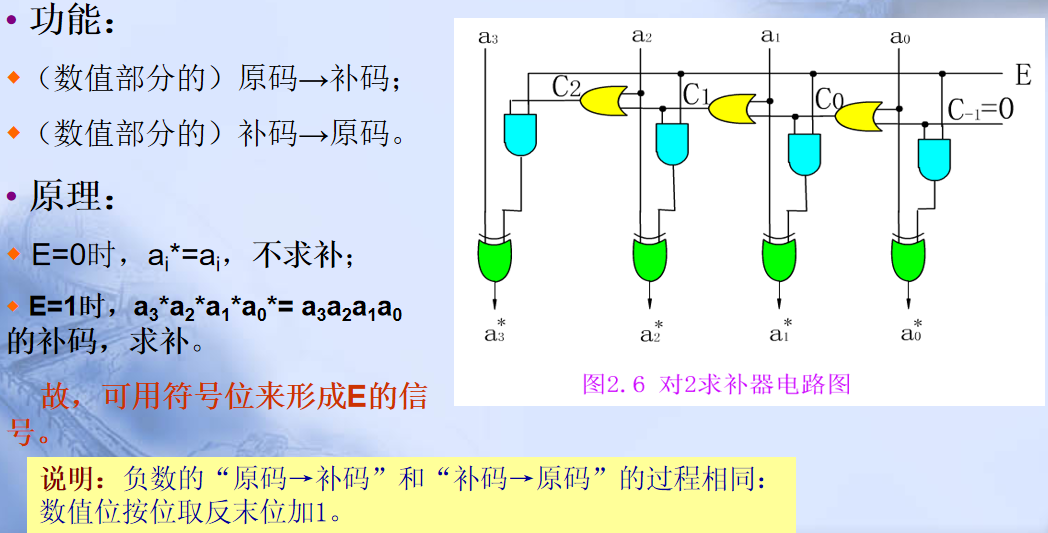
3.算前(后)求补器的功能和实现电路:
间接补码并行乘法的例子:

(2)直接补码并行乘法
2.4定点除法运算


一、(串行)恢复余数法:


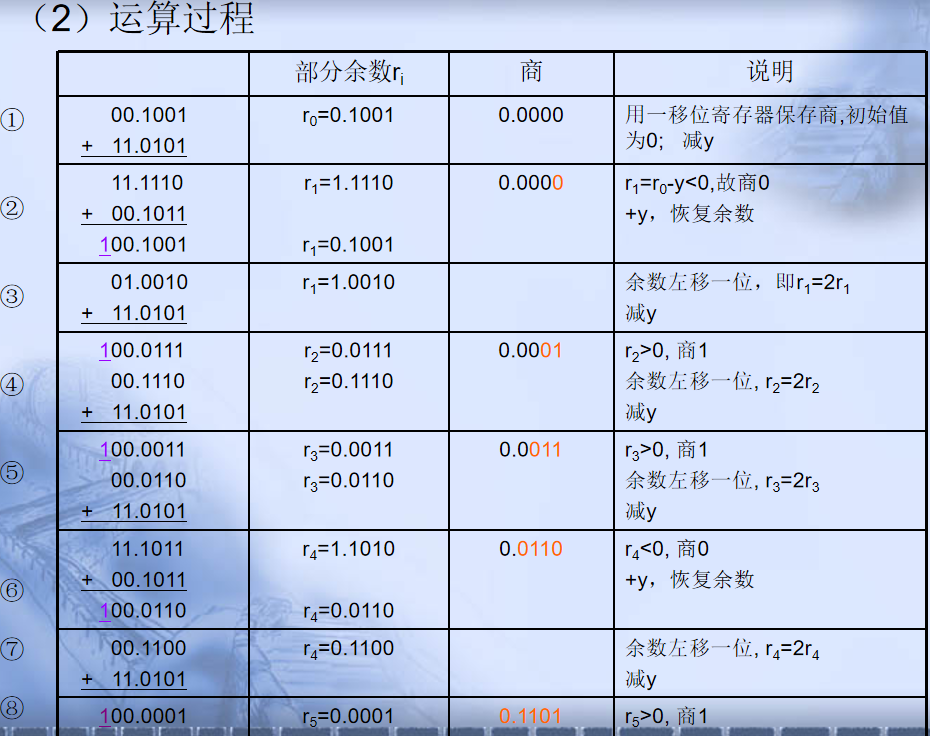
二、不恢复余数法(加减交替法)


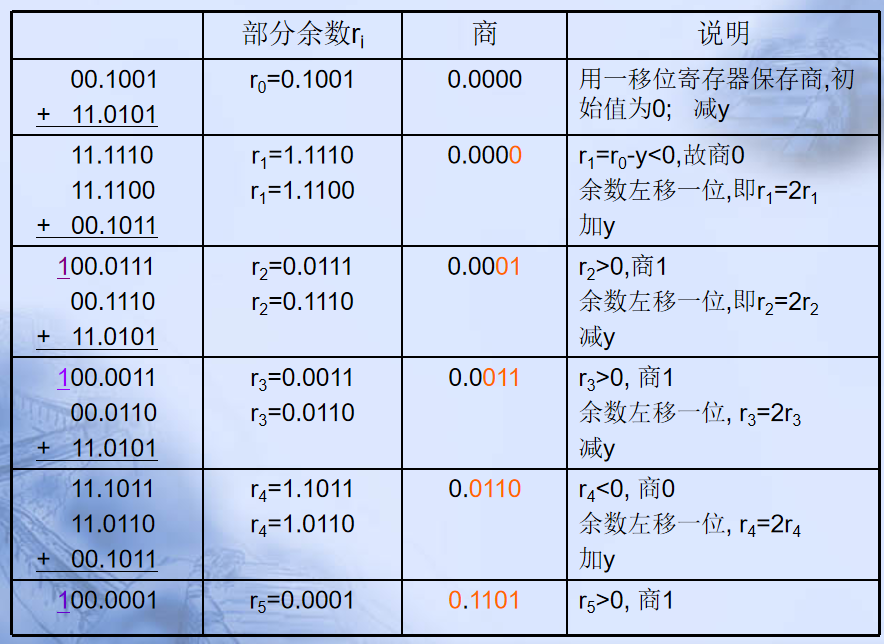

三、(并行)不恢复余数的阵列除法器


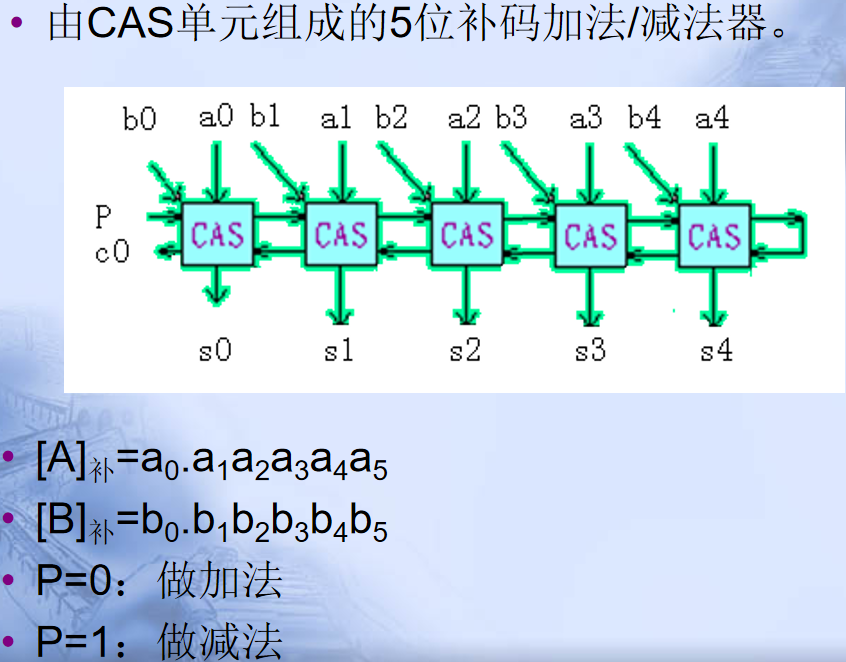
2.5定点运算器的组成
一、逻辑运算
分:逻辑非、逻辑加(逻辑或)、逻辑乘(逻辑与)、逻辑异(异或)四种基本运算
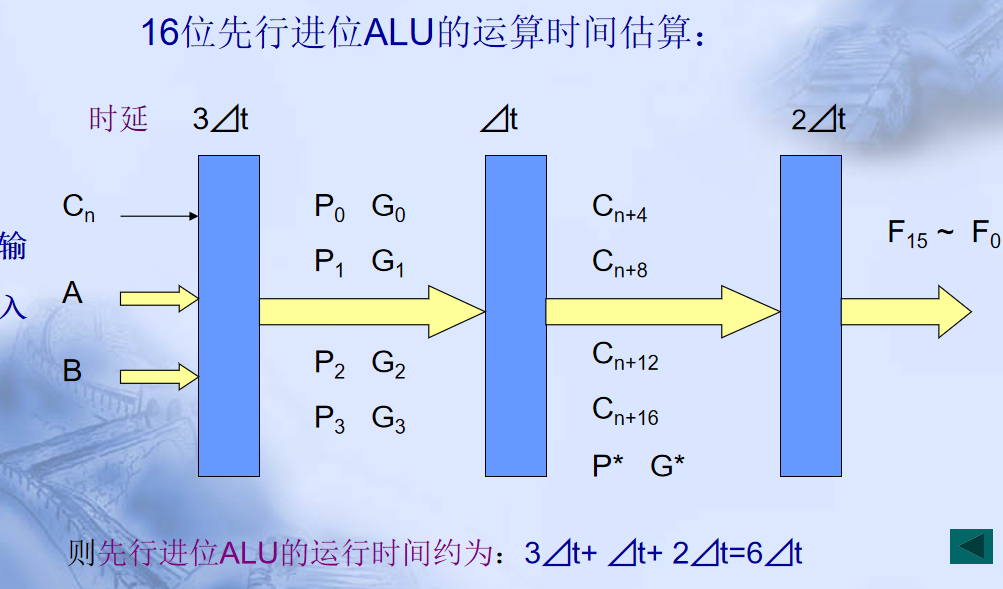
二、多功能算术/逻辑运算单元ALU
1.先行进位算法
(1)一位全加器: (2) 由一位全加器构成的串行进位的四位加法器 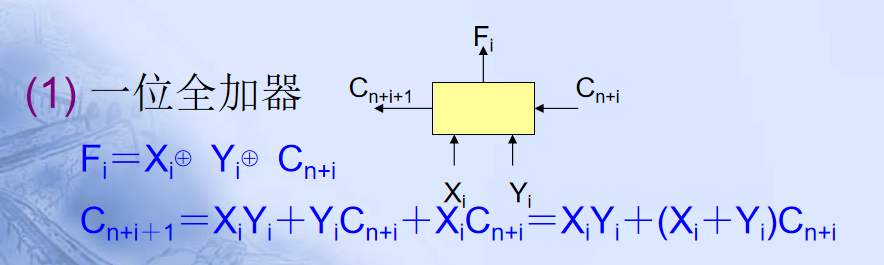
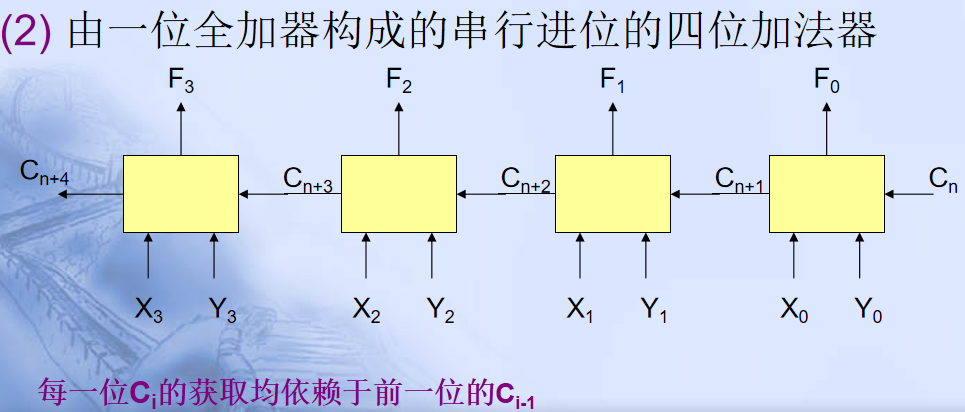
Cn+1~ Cn+4是同时算出的,故比串行进位的全加器速度要快。依此先行进位公式,可设计出四位并行加法器。对全加器电路再增加一函数发生器电路,即 可实现多种算术运算。
2.多种算术运算的实现:
可以证明:XiYi=Yi, Xi+Yi=Xi,则Cn+1=Y0+X0Cn,······Cn+4=Y3+ Y2X3 +Y1X2 X3 +Y0X1X2 X3 +X0X1X2X3Cn
=G+PCn G= Y3+ Y2X3 +Y1X2 X3 +Y0X1X2 X3 , P=X0X1X2X3

3. 算术/逻辑运算单元74181ALU
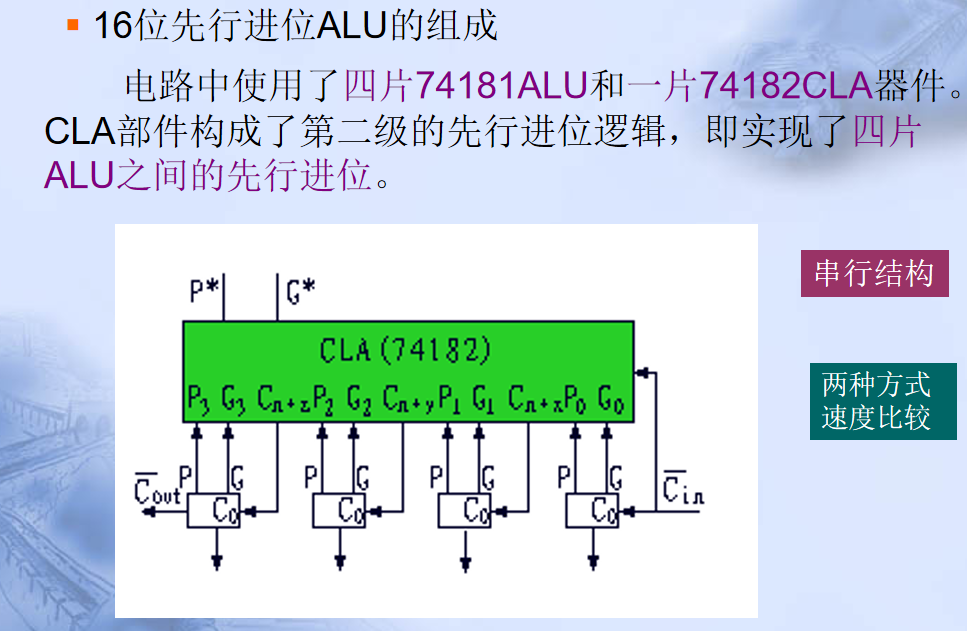
三、内部总线
内部总线:CPU内各部分的连线,分单向、双向总线
四、定点运算器的基本结构
运算器包括ALU、阵列乘除器、寄存器、多路开关、三态缓冲器、数据总线等逻辑部件。
1.单总线结构的运算器:双操作数分时经总线进入锁存器A和B,结果也通过单总线送回
2.双总线结构的运算器:两操作数通过各自的总线送加法器运算,结果通过 其中一总线送回
3.三总线结构的运算器:两操作数和操作结果通过各自的总线传送

2.6浮点运算方法和浮点运算器
一、浮点加减法运算
1.对(补码)非规格化数的规格化处理:

2.浮点加减法运算过程:

运算步骤:1对阶 2尾数求和 3规格化
小阶向大阶看齐:尾数右移,损失的是最小位
舍入处理:在对阶或者是右规的时候尾数要右移,舍弃低位,有两种舍入处理方法:“0舍1入法”,舍入的部分最高位为1的话就进一个1,最高位为0的话就直接舍去;“恒置1法”,只要位数被移掉,就在尾数末尾加“1”。
溢出处理:浮点数的溢出是按照阶码是否溢出来判断的!!!
数的表示:一般阶码E采用移码或补码表示,而尾数M采用补码表示。

二、浮点乘除法运算
1.浮点数的阶码运算:


2.对尾数运算结果(Mx× My)的处理:

运算步骤:1.0操作数检查 2.阶码加/减操作 3.尾数乘/除操作 4.结果规格化及舍入处理


三、浮点运算流水线:
各子过程段之间须设置高速缓冲存储器。


