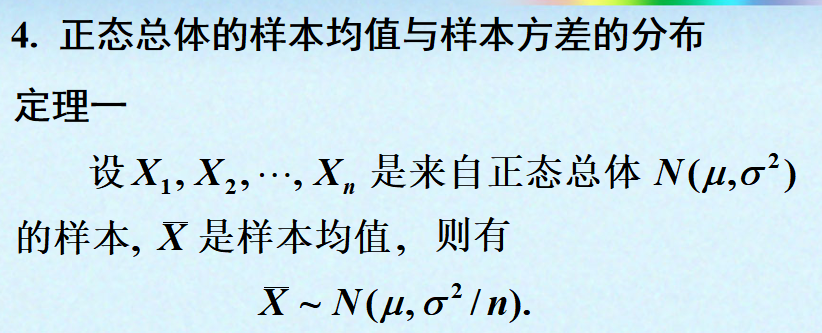概率论复习

概率论主要就是把公式提取出来了

不记公式星人又要展示考前临时速记，考完就忘操作啦~

 

 

1.若X是一维连续型随机变量，且Y=g(X)是关于X的单调函数，那么设h(y)为Y=g(X)的反函数：

 

 2连续性随机变量的函数的数学期望：

.

3.二维随机变量函数的数学期望：

        

 

 4.相互独立的随机变量：

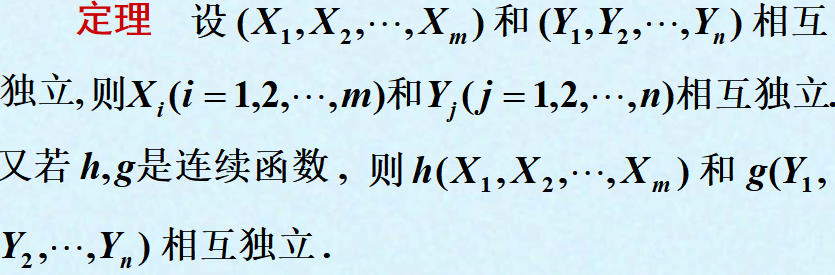
 5.条件分布函数与条件密度函数的关系：

 

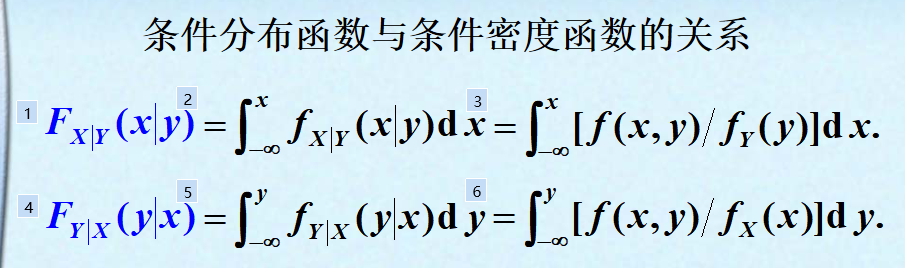
 6.两个连续性随机变量函数的分布：

 

一个重要公式：

 

 

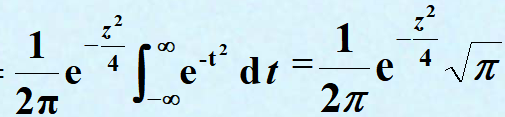
 有限个相互独立的正态随机变量的线性组合仍服从正态分布。

 

 

 

 

 

 7.方差：

 

 

 

切比雪夫不等式给出了在随机变量的分布未知，而只知道E(X)和D(X)的情况下估计概率P{|X-E(X)|<}的界限的方法。

 

 8.协方差和相关系数：

 

 

 

 

 

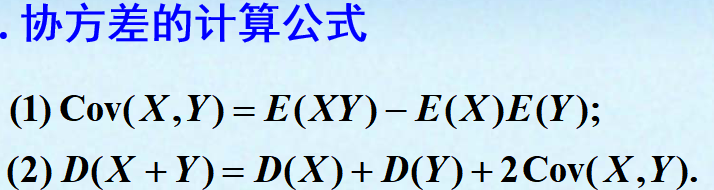
中心极限定理：

独立同分布的中心极限定理：（条件：同分布、相互独立、同期望、同方差）

李雅普诺夫定理：（条件：只需要相互独立）

用棣莫弗—拉普拉斯定理求值：（条件：同两点分布）

 

 

 

 

 随机样本：

 

 两点分布的分布律可以写成：

 

分位点：

 

 

 

 

 

 

 

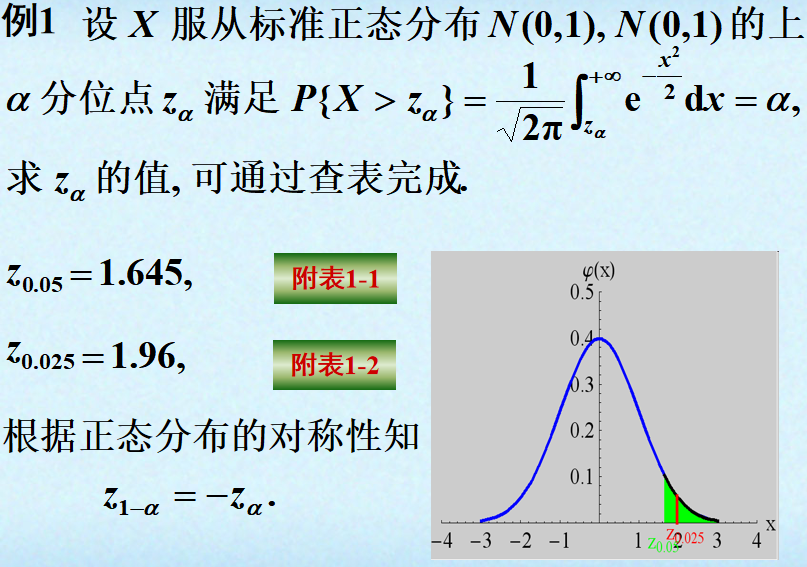
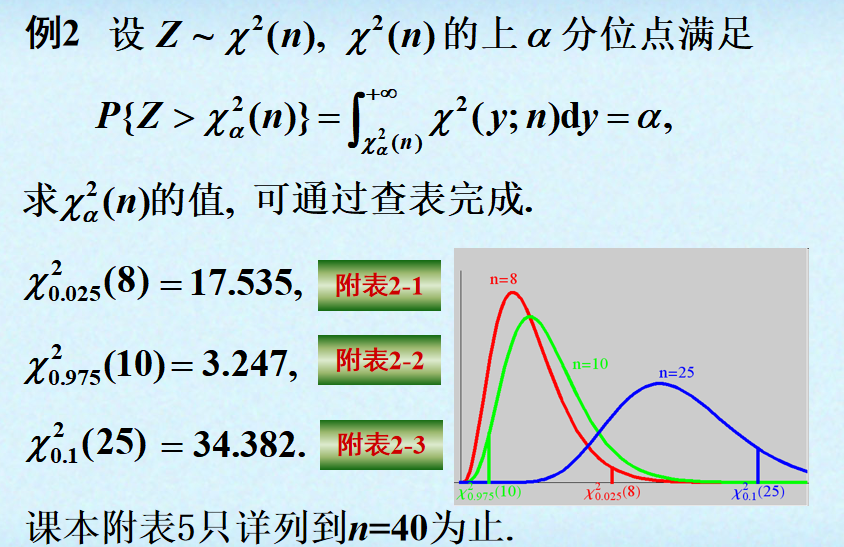
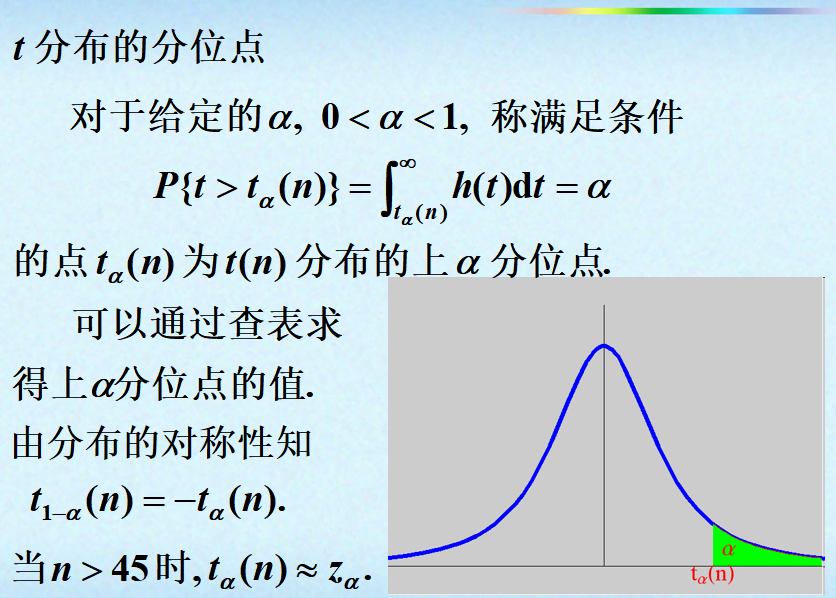
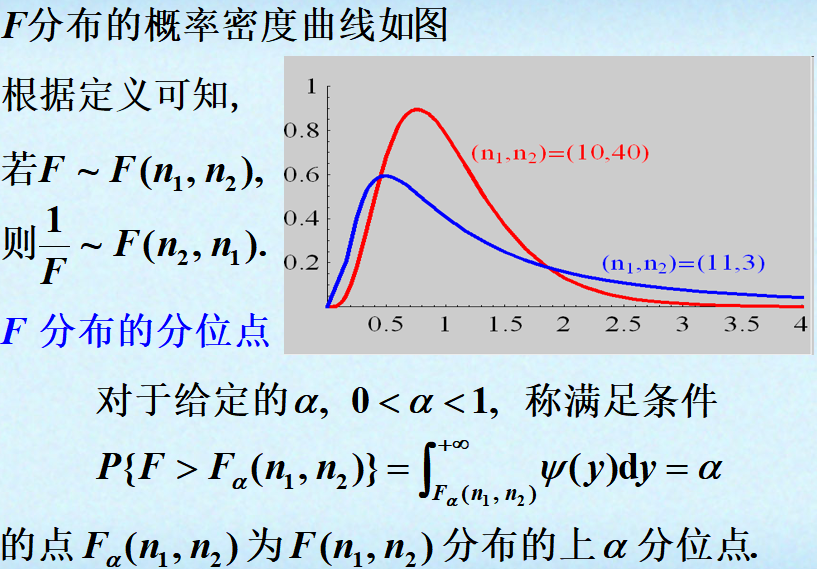
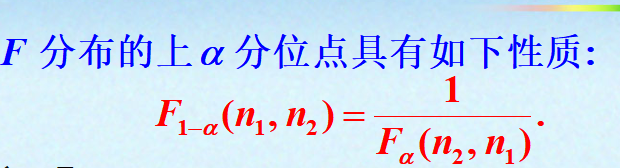
 正态总体的样本均值与样本方差：