Neural Network模型复杂度之Residual Block - Python实现
-
背景介绍
Neural Network之模型复杂度主要取决于优化参数个数与参数变化范围. 优化参数个数可手动调节, 参数变化范围可通过正则化技术加以限制. 本文从优化参数个数出发, 以Residual Block技术为例, 简要演示Residual Block残差块对Neural Network模型复杂度的影响. -
算法特征
①. 对输入进行等维度变换; ②. 以加法连接前后变换扩大函数空间 -
算法推导
典型残差块结构如下,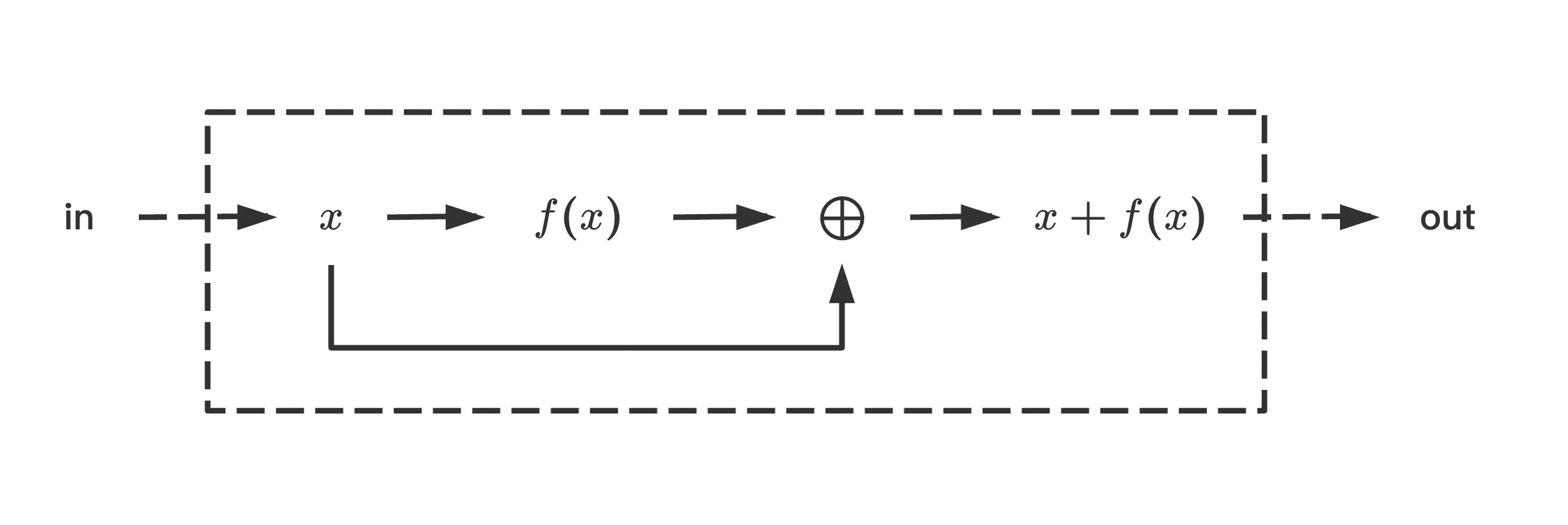
即, 输入\(x\)之函数空间通过加法\(x + f(x)\)扩大. 可以看到, 在前向计算过程中, 函数\(f(x)\)之作用类似于残差, 补充输入\(x\)对标准输出描述之不足; 同时, 在反向传播过程中, 对输入\(x\)之梯度计算分裂在不同影响链路上, 降低了函数\(f(x)\)对梯度的直接影响.
-
数据、模型与损失函数
数据生成策略如下,\[\left\{ \begin{align*} x &= r + 2g + 3b \\ y &= r^2 + 2g^2 + 3b^2 \\ lv &= -3r - 4g - 5b \end{align*} \right. \]Neural Network网络模型如下,
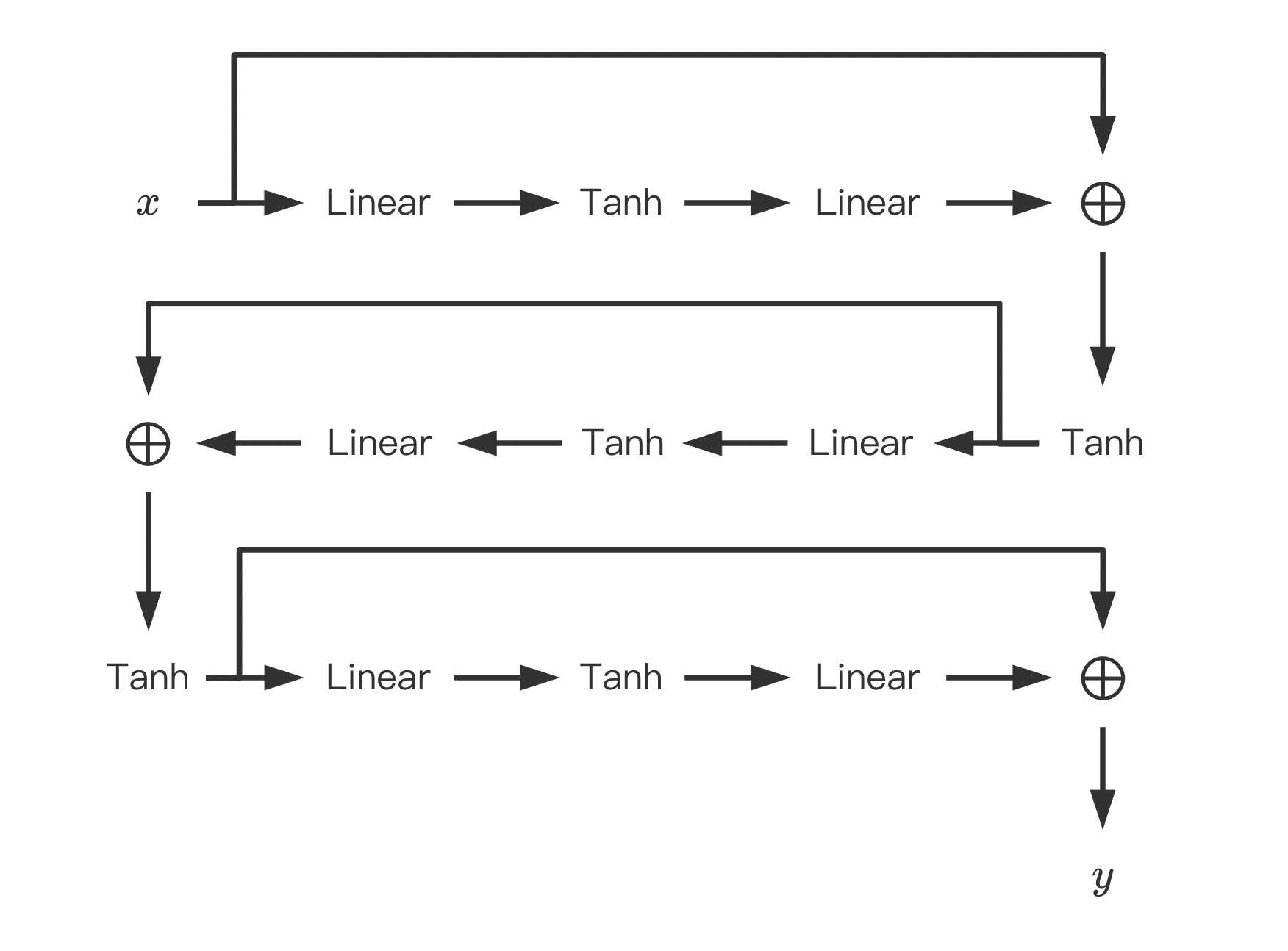
其中, 输入层\(x:=(r, g, b)\), 输出层\(y:=(x, y, lv)\), 中间所有隐藏层与输入之dimension保持一致.
损失函数如下,\[L = \sum_{i}\frac{1}{2}(\bar{x}^{(i)} - x^{(i)})^2 + \frac{1}{2}(\bar{y}^{(i)} - y^{(i)})^2 + \frac{1}{2}(\bar{lv}^{(i)} - lv^{(i)})^2 \]其中, \(i\)为data序号, \((\bar{x}, \bar{y}, \bar{lv})\)为相应观测值.
-
代码实现
本文以是否采用Residual Block为例(即在上述模型中是否去除\(\oplus\)), 观察Residual Block对模型复杂度的影响.code
import numpy import torch from torch import nn from torch import optim from torch.utils import data from matplotlib import pyplot as plt numpy.random.seed(0) # 获取数据与封装数据 def xFunc(r, g, b): x = r + 2 * g + 3 * b return x def yFunc(r, g, b): y = r ** 2 + 2 * g ** 2 + 3 * b ** 2 return y def lvFunc(r, g, b): lv = -3 * r - 4 * g - 5 * b return lv class GeneDataset(data.Dataset): def __init__(self, rRange=[-1, 1], gRange=[-1, 1], bRange=[-1, 1], \ num=100, transform=None, target_transform=None): self.__rRange = rRange self.__gRange = gRange self.__bRange = bRange self.__num = num self.__transform = transform self.__target_transform = target_transform self.__X = self.__build_X() self.__Y_ = self.__build_Y_() def __build_Y_(self): rArr = self.__X[:, 0:1] gArr = self.__X[:, 1:2] bArr = self.__X[:, 2:3] xArr = xFunc(rArr, gArr, bArr) yArr = yFunc(rArr, gArr, bArr) lvArr = lvFunc(rArr, gArr, bArr) Y_ = numpy.hstack((xArr, yArr, lvArr)) return Y_ def __build_X(self): rArr = numpy.random.uniform(*self.__rRange, (self.__num, 1)) gArr = numpy.random.uniform(*self.__gRange, (self.__num, 1)) bArr = numpy.random.uniform(*self.__bRange, (self.__num, 1)) X = numpy.hstack((rArr, gArr, bArr)) return X def __len__(self): return self.__num def __getitem__(self, idx): x = self.__X[idx] y_ = self.__Y_[idx] if self.__transform: x = self.__transform(x) if self.__target_transform: y_ = self.__target_transform(y_) return x, y_ # 构建模型 class Model(nn.Module): def __init__(self, is_residual_block=True): super(Model, self).__init__() torch.random.manual_seed(0) self.__is_residual_block = is_residual_block self.__in_features = 3 self.__out_features = 3 self.lin11 = nn.Linear(3, 3, dtype=torch.float64) self.lin12 = nn.Linear(3, 3, dtype=torch.float64) self.lin21 = nn.Linear(3, 3, dtype=torch.float64) self.lin22 = nn.Linear(3, 3, dtype=torch.float64) self.lin31 = nn.Linear(3, 3, dtype=torch.float64) self.lin32 = nn.Linear(3, 3, dtype=torch.float64) def forward(self, X): X1 = self.lin12(torch.tanh(self.lin11(X))) if self.__is_residual_block: X1 += X X1 = torch.tanh(X1) X2 = self.lin22(torch.tanh(self.lin21(X1))) if self.__is_residual_block: X2 += X1 X2 = torch.tanh(X2) X3 = self.lin32(torch.tanh(self.lin31(X2))) if self.__is_residual_block: X3 += X2 return X3 # 构建损失函数 class MSE(nn.Module): def forward(self, Y, Y_): loss = torch.sum((Y - Y_) ** 2) return loss # 训练单元与测试单元 def train_epoch(trainLoader, model, loss_fn, optimizer): model.train(True) loss = 0 with torch.enable_grad(): for X, Y_ in trainLoader: optimizer.zero_grad() Y = model(X) lossVal = loss_fn(Y, Y_) lossVal.backward() optimizer.step() loss += lossVal.item() loss /= len(trainLoader.dataset) return loss def test_epoch(testLoader, model, loss_fn, optimzier): model.train(False) loss = 0 with torch.no_grad(): for X, Y_ in testLoader: Y = model(X) lossVal = loss_fn(Y, Y_) loss += lossVal.item() loss /= len(testLoader.dataset) return loss def train_model(trainLoader, testLoader, epochs=100): model_RB = Model(True) loss_RB = MSE() optimizer_RB = optim.Adam(model_RB.parameters(), 0.001) model_No = Model(False) loss_No = MSE() optimizer_No = optim.Adam(model_No.parameters(), 0.001) trainLoss_RBList = list() testLoss_RBList = list() trainLoss_NoList = list() testLoss_NoList = list() for epoch in range(epochs): trainLoss_RB = train_epoch(trainLoader, model_RB, loss_RB, optimizer_RB) testLoss_RB = test_epoch(testLoader, model_RB, loss_RB, optimizer_RB) trainLoss_No = train_epoch(trainLoader, model_No, loss_No, optimizer_No) testLoss_No = test_epoch(testLoader, model_No, loss_No, optimizer_No) trainLoss_RBList.append(trainLoss_RB) testLoss_RBList.append(testLoss_RB) trainLoss_NoList.append(trainLoss_No) testLoss_NoList.append(testLoss_No) if epoch % 50 == 0: print(epoch, trainLoss_RB, trainLoss_No, testLoss_RB, testLoss_No) fig = plt.figure(figsize=(5, 4)) ax1 = fig.add_subplot(1, 1, 1) X = numpy.arange(1, epochs+1) ax1.plot(X, trainLoss_RBList, "r-", lw=1, label="train with RB") ax1.plot(X, testLoss_RBList, "r--", lw=1, label="test with RB") ax1.plot(X, trainLoss_NoList, "b-", lw=1, label="train without RB") ax1.plot(X, testLoss_NoList, "b--", lw=1, label="test without RB") ax1.set(xlabel="epoch", ylabel="loss", yscale="log") ax1.legend() fig.tight_layout() fig.savefig("loss.png", dpi=300) plt.show() if __name__ == "__main__": trainData = GeneDataset([-1, 1], [-1, 1], [-1, 1], num=1000, \ transform=torch.tensor, target_transform=torch.tensor) testData = GeneDataset([-1, 1], [-1, 1], [-1, 1], num=300, \ transform=torch.tensor, target_transform=torch.tensor) trainLoader = data.DataLoader(trainData, batch_size=len(trainData), shuffle=False) testLoader = data.DataLoader(testData, batch_size=len(testData), shuffle=False) epochs = 10000 train_model(trainLoader, testLoader, epochs) -
结果展示
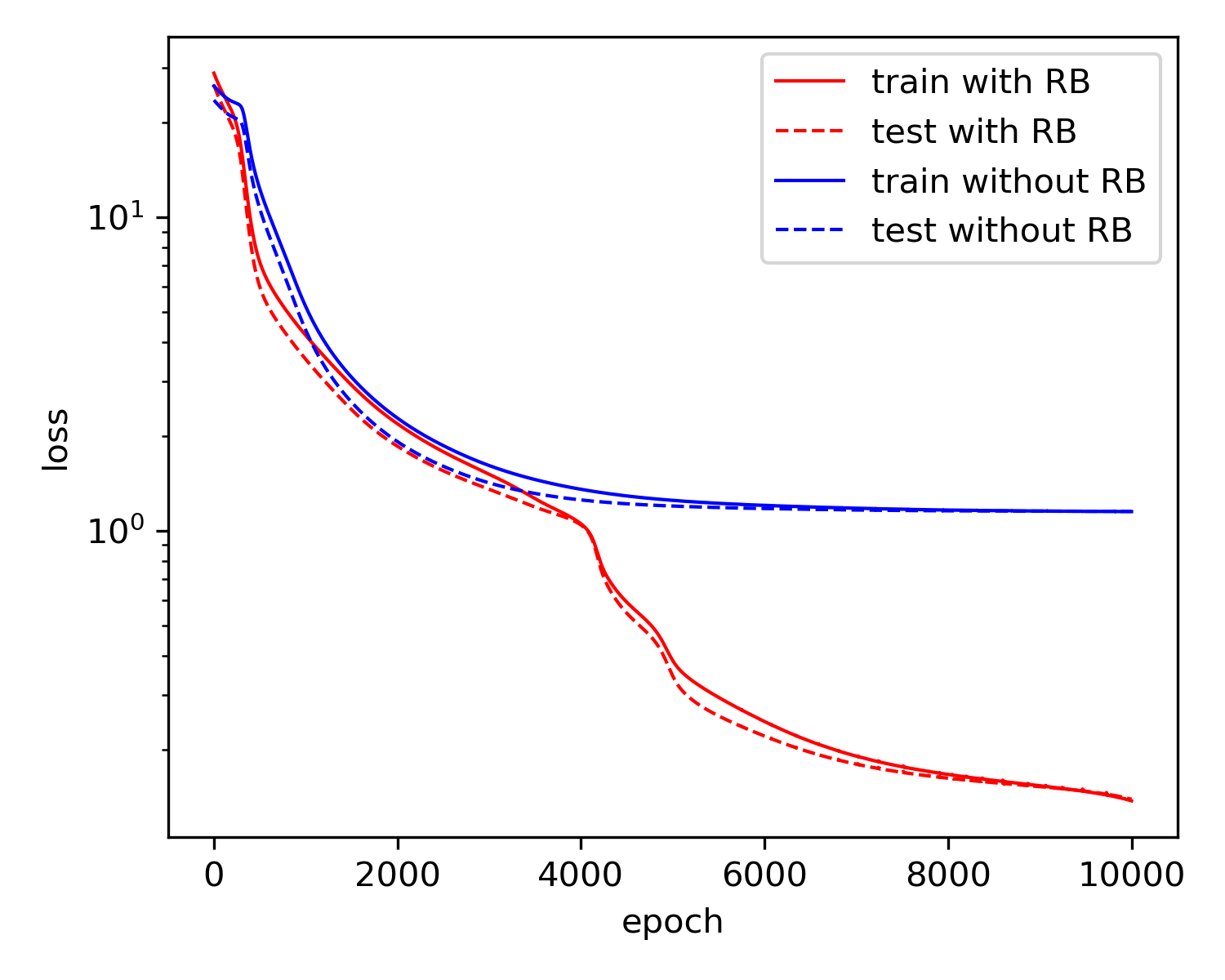
可以看到, 由于Residual Block结构引入额外的优化参数, 模型复杂度得以提升. 同时, 相较于常规Neural Network(对应去除Residual Block之\(\oplus\)), Residual Block之Neural Network在优化参数个数相同的前提下更加稳妥地扩大了函数空间.
-
使用建议
①. 残差函数之设计应当具备与目标输出匹配之能力;
②. 残差函数之设计可改变dimension, 此时\(\oplus\)侧之输入应当进行线性等维调整;
③. 若训练数据之复杂度高于测试数据, 则在训练起始, 训练数据之loss可能也要高于测试数据. -
参考文档
①. 动手学深度学习 - 李牧




