Neural Network模型复杂度之Dropout - Python实现

• 背景介绍
  Neural Network之模型复杂度主要取决于优化参数个数与参数变化范围. 优化参数个数可手动调节, 参数变化范围可通过正则化技术加以限制. 本文从优化参数个数出发, 以dropout技术为例, 简要演示dropout参数丢弃比例对Neural Network模型复杂度的影响.

• 算法特征
  ①. 训练阶段以概率丢弃数据点; ②. 测试阶段保留所有数据点

• 算法推导
  以概率\(p\)对数据点\(x\)进行如下变换,

  \[\begin{equation*} x' = \left\{\begin{split} &0 &\quad\text{with probability $p$,} \\ &\frac{x}{1-p} &\quad\text{otherwise,} \end{split}\right. \end{equation*} \]

  即数据点\(x\)以概率\(p\)置零, 以概率\(1-p\)放大\(1/(1-p)\)倍. 此时有,

  \[\begin{equation*} \mathbf{E}[x'] = p\mathbf{E}[0] + (1-p)\mathbf{E}[\frac{x}{1-p}] = \mathbf{E}[x], \end{equation*} \]

  此变换不改变数据点均值, 为无偏变换.
  若数据点\(x\)作为某线性变换之输入, 将其置零, 则对此线性变换无贡献, 等效于无效化该数据点及相关权重参数, 减少了优化参数个数, 降低了模型复杂度.

• 数据、模型与损失函数
  数据生成策略如下,

  \[\begin{equation*} \left\{\begin{aligned} x &= r + 2g + 3b \\ y &= r^2 + 2g^2 + 3b^2 \\ lv &= -3r - 4g - 5b \end{aligned}\right. \end{equation*} \]

  Neural Network网络模型如下,

  
  其中, 输入层为$(r, g, b)$, 隐藏层取激活函数$\tanh$, 输出层为$(x, y, lv)$且不取激活函数.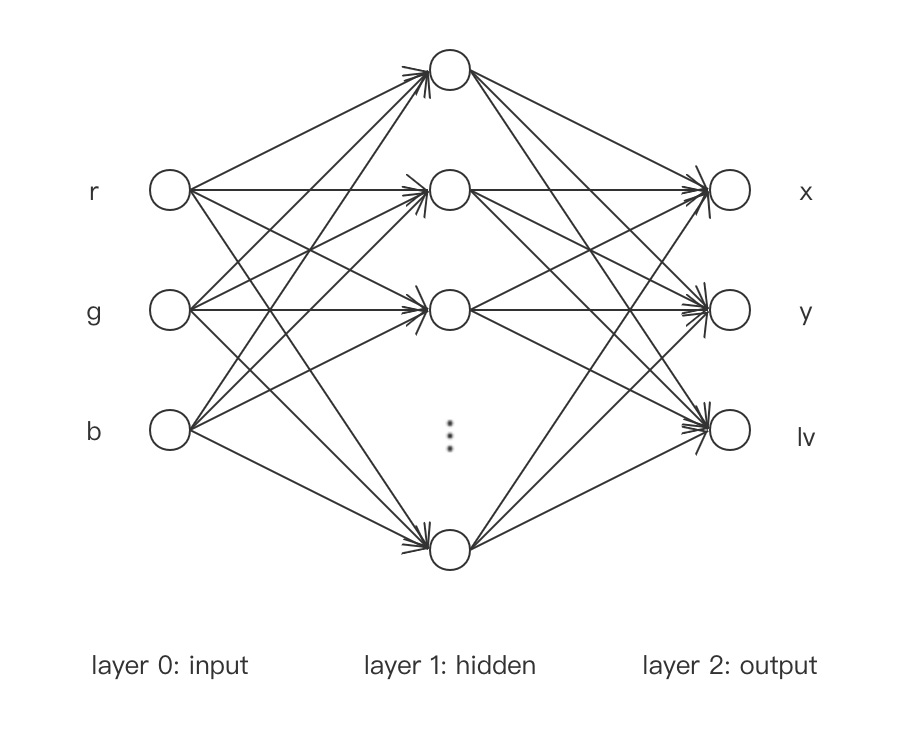
  损失函数如下, $$ \begin{equation*} L = \sum_i\frac{1}{2}(\bar{x}^{(i)}-x^{(i)})^2+\frac{1}{2}(\bar{y}^{(i)}-y^{(i)})^2+\frac{1}{2}(\bar{lv}^{(i)}-lv^{(i)})^2 \end{equation*} $$ 其中, $i$为data序号, $(\bar{x}, \bar{y}, \bar{lv})$为相应观测值.

• 代码实现
  本文拟将中间隐藏层节点数设置为300, 使模型具备较高复杂度. 后逐步提升置零概率\(p\), 使模型复杂度降低, 以此观察泛化误差的变化. 具体实现如下,

  code

  import numpy
  import torch
  from torch import nn
  from torch import optim
  from torch.utils import data
  from matplotlib import pyplot as plt
  
  
  # 获取数据与封装数据
  def xFunc(r, g, b):
      x = r + 2 * g + 3 * b
      return x
  
  
  def yFunc(r, g, b):
      y = r ** 2 + 2 * g ** 2 + 3 * b ** 2
      return y
  
  
  def lvFunc(r, g, b):
      lv = -3 * r - 4 * g - 5 * b
      return lv
  
  
  class GeneDataset(data.Dataset):
      
      def __init__(self, rRange=[-1, 1], gRange=[-1, 1], bRange=[-1, 1], num=100, transform=None,\
                   target_transform=None):
          self.__rRange = rRange
          self.__gRange = gRange
          self.__bRange = bRange
          self.__num = num
          self.__transform = transform
          self.__target_transform = transform
          
          self.__X = self.__build_X()
          self.__Y_ = self.__build_Y_()
          
      
      def __build_X(self):
          rArr = numpy.random.uniform(*self.__rRange, (self.__num, 1))
          gArr = numpy.random.uniform(*self.__gRange, (self.__num, 1))
          bArr = numpy.random.uniform(*self.__bRange, (self.__num, 1))
          X = numpy.hstack((rArr, gArr, bArr))
          return X
      
      
      def __build_Y_(self):
          rArr = self.__X[:, 0:1]
          gArr = self.__X[:, 1:2]
          bArr = self.__X[:, 2:3]
          xArr = xFunc(rArr, gArr, bArr)
          yArr = yFunc(rArr, gArr, bArr)
          lvArr = lvFunc(rArr, gArr, bArr)
          Y_ = numpy.hstack((xArr, yArr, lvArr))
          return Y_
      
      
      def __len__(self):
          return self.__num
      
      
      def __getitem__(self, idx):
          x = self.__X[idx]
          y_ = self.__Y_[idx]
          if self.__transform:
              x = self.__transform(x)
          if self.__target_transform:
              y_ = self.__target_transform(y_)
          return x, y_
  
  
  # 构建模型
  class Linear(nn.Module):
      
      def __init__(self, dim_in, dim_out):
          super(Linear, self).__init__()
          
          self.__dim_in = dim_in
          self.__dim_out = dim_out
          self.weight = nn.Parameter(torch.randn((dim_in, dim_out)))
          self.bias = nn.Parameter(torch.randn((dim_out,)))
          
          
      def forward(self, X):
          X = torch.matmul(X, self.weight) + self.bias
          return X
      
      
  class Tanh(nn.Module):
      
      def __init__(self):
          super(Tanh, self).__init__()
          
          
      def forward(self, X):
          X = torch.tanh(X)
          return X
  
  
  class Dropout(nn.Module):
      
      def __init__(self, p):
          super(Dropout, self).__init__()
          
          assert 0 <= p <= 1
          self.__p = p     # 置零概率
          
          
      def forward(self, X):
          if self.__p == 0:
              return X
          if self.__p == 1:
              return torch.zeros_like(X)
          mark = (torch.rand(X.shape) > self.__p).type(torch.float)
          X = X * mark / (1 - self.__p)
          return X
      
  
  class MLP(nn.Module):
      
      def __init__(self, dim_hidden=50, p=0, is_training=True):
          super(MLP, self).__init__()
          
          self.__dim_hidden = dim_hidden
          self.__p = p
          self.training = True
          self.__dim_in = 3
          self.__dim_out = 3
          
          self.lin1 = Linear(self.__dim_in, self.__dim_hidden)
          self.tanh = Tanh()
          self.drop = Dropout(self.__p)
          self.lin2 = Linear(self.__dim_hidden, self.__dim_out)
  
          
      def forward(self, X):
          X = self.tanh(self.lin1(X))
          if self.training:
              X = self.drop(X)
          X = self.lin2(X)
          return X
  
  
  # 构建损失函数
  class MSE(nn.Module):
          
      def __init__(self):
          super(MSE, self).__init__()
          
          
      def forward(self, Y, Y_):
          loss = torch.sum((Y - Y_) ** 2) / 2
          return loss
  
  
  # 训练单元与测试单元
  def train_epoch(trainLoader, model, loss_fn, optimizer):
      model.train()
      loss = 0
      
      with torch.enable_grad():
          for X, Y_ in trainLoader:
              optimizer.zero_grad()
              Y = model(X)
              loss_tmp = loss_fn(Y, Y_)
              loss_tmp.backward()
              optimizer.step()
              
              loss += loss_tmp.item()
      return loss
              
          
  def test_epoch(testLoader, model, loss_fn):
      model.eval()
      loss = 0
      
      with torch.no_grad():
          for X, Y_ in testLoader:
              Y = model(X)
              loss_tmp = loss_fn(Y, Y_)
              loss += loss_tmp.item()
              
      return loss
  
  
  # 进行训练与测试
  def train(trainLoader, testLoader, model, loss_fn, optimizer, epochs):
      minLoss = numpy.inf
      for epoch in range(epochs):
          trainLoss = train_epoch(trainLoader, model, loss_fn, optimizer) / len(trainLoader.dataset)
          testLoss = test_epoch(testLoader, model, loss_fn) / len(testLoader.dataset)
          if testLoss < minLoss:
              minLoss = testLoss
              torch.save(model.state_dict(), "./mlp.params")
  #         if epoch % 100 == 0:
  #             print(f"epoch = {epoch:8}, trainLoss = {trainLoss:15.9f}, testLoss = {testLoss:15.9f}")
      return minLoss
  
  
  numpy.random.seed(0)
  torch.random.manual_seed(0)
  
  def search_dropout():
      trainData = GeneDataset(num=50, transform=torch.Tensor, target_transform=torch.Tensor)
      trainLoader = data.DataLoader(trainData, batch_size=50, shuffle=True)
      testData = GeneDataset(num=1000, transform=torch.Tensor, target_transform=torch.Tensor)
      testLoader = data.DataLoader(testData, batch_size=1000, shuffle=False)
  
      dim_hidden1 = 300
      p = 0.005
      model = MLP(dim_hidden1, p)
      loss_fn = MSE()
      optimizer = optim.Adam(model.parameters(), lr=0.003)
      train(trainLoader, testLoader, model, loss_fn, optimizer, 100000)
  
      pRange = numpy.linspace(0, 1, 101)
      lossList = list()
      for idx, p in enumerate(pRange):
          model = MLP(dim_hidden1, p)
          loss_fn = MSE()
          optimizer = optim.Adam(model.parameters(), lr=0.003)
          model.load_state_dict(torch.load("./mlp.params"))
          loss = train(trainLoader, testLoader, model, loss_fn, optimizer, 100000)
          lossList.append(loss)
          print(f"p = {p:10f}, loss = {loss:15.9f}")
  
      minIdx = numpy.argmin(lossList)
      pBest = pRange[minIdx]
      lossBest = lossList[minIdx]
  
      fig = plt.figure(figsize=(5, 4))
      ax1 = fig.add_subplot(1, 1, 1)
      ax1.plot(pRange, lossList, ".--", lw=1, markersize=5, label="testing error", zorder=1)
      ax1.scatter(pBest, lossBest, marker="*", s=30, c="red", label="optimal", zorder=2)
      ax1.set(xlabel="$p$", ylabel="error", title="optimal dropout probability = {:.5f}".format(pBest))
      ax1.legend()
      fig.tight_layout()
      fig.savefig("search_p.png", dpi=100)
      # plt.show()
  
  
  
  if __name__ == "__main__":
      search_dropout()
  

• 结果展示

  
  可以看到, 泛化误差在提升置零概率后先下降后上升, 大致对应降低模型复杂度使模型表现从过拟合至欠拟合.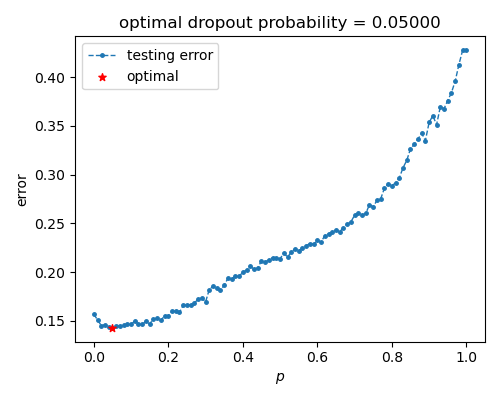

• 使用建议
  ①. dropout为使整个节点失效, 通常作用在节点的最终输出上(即激活函数后);
  ②. dropout适用于神经网络全连接层.

• 参考文档
  ①. 动手学深度学习 - 李牧