Neural Network模型复杂度之Weight Decay - Python实现

  • 背景介绍
    Neural Network之模型复杂度主要取决于优化参数个数与参数变化范围. 优化参数个数可手动调节, 参数变化范围可通过正则化技术加以限制. 正则化技术之含义是: 引入额外的条件, 对function space进行适当的约束. 本文借助pytorch前向计算与反向传播特性, 以正则化技术之weight decay($l^2$范数)为例, 简要演示正则化对Neural Network模型复杂度的影响.
  • 操作流程
    ①. 获取数据; ②. 封装数据; ③. 构建模型; ④. 构建损失函数; ⑤. 构建优化器; ⑥. 训练单元; ⑦. 测试单元; ⑧. 启动训练测试; ⑨. 保存模型
  • 数据、模型与损失函数
    数据生成策略如下,
    \begin{equation*}
    \left\{
    \begin{aligned}
    x &= r + 2g + 3b \\
    y &= r^2 + 2g^2 + 3b^2 \\
    lv &= -3r-4g-5b
    \end{aligned}
    \right.
    \end{equation*}
    Neural Network网络模型如下,
     其中, 输入层为$(r,g,b)$, 隐藏层取激活函数为双曲正切函数$\tanh$, 输出层为$(x,y,lv)$且不取激活函数.
    损失函数如下,
    \begin{gather*}
    L = \sum_i\frac{1}{2}(\bar{x}^{(i)}-x^{(i)})^2+\frac{1}{2}(\bar{y}^{(i)}-y^{(i)})^2+\frac{1}{2}(\bar{lv}^{(i)}-lv^{(i)})^2 \\
    J = L + \frac{\lambda}{2}\|W\|_2^2
    \end{gather*}
    其中, $i$为data序号, $(\bar{x}, \bar{y}, \bar{lv})$为相应观测值, $W$为隐藏层weight, $L$为原始损失函数, $J$为添加$W$之$l^2$正则项后的损失函数, $\lambda$为可调超参数控制正则项在损失函数$J$中的权重.
  • 代码实现
    本文拟将中间隐藏层节点数设置为50, 使模型具备较高复杂度. 后逐渐提升权重参数$\lambda$, 使模型复杂度降低, 以此观察泛化误差的变化. 根据操作流程, 具体实现如下,
      1 # L2 normalization之实现:
  2 # 1. 获取数据
  3 # 2. 封装数据
  4 # 3. 构建模型
  5 # 4. 构建损失函数
  6 # 5. 构建优化器
  7 # 6. 训练单元
  8 # 7. 测试单元
  9 # 8. 启动训练与测试
 10 # 9. 保存模型
 11 
 12 import numpy
 13 import torch
 14 from torch import optim
 15 from matplotlib import pyplot as plt
 16 
 17 
 18 numpy.random.seed(0)
 19 torch.random.manual_seed(0)
 20 
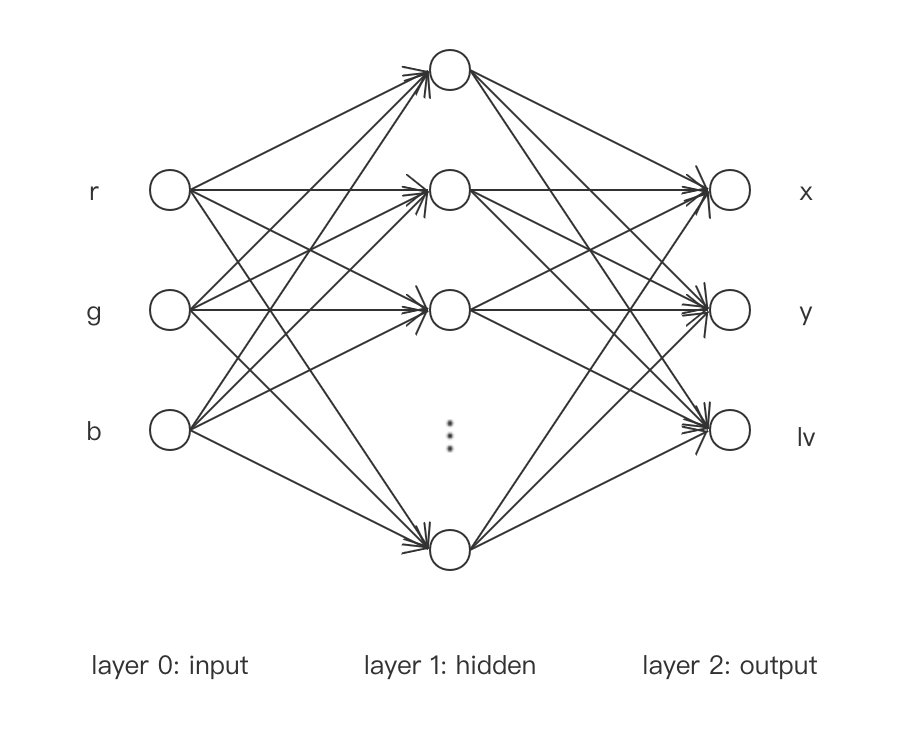
 21 def xFunc(r, g, b):
 22     x = r + 2 * g + 3 * b
 23     return x
 24 
 25 def yFunc(r, g, b):
 26     y = r ** 2 + 2 * g ** 2 + 3 * b ** 2
 27     return y
 28 
 29 def lvFunc(r, g, b):
 30     lv = -3 * r - 4 * g - 5 * b
 31     return lv
 32 
 33 
 34 # 1. 获取数据
 35 class GeneData(object):
 36 
 37     def __init__(self, rRange=[-1, 1], gRange=[-1, 1], bRange=[-1, 1]):
 38         self.__rRange = rRange
 39         self.__gRange = gRange
 40         self.__bRange = bRange
 41 
 42     def getDataset(self, num):
 43         rArr, gArr, bArr = self.__generate_rgbArr(num)
 44         xArr, yArr, lvArr = self.__generate_xylvArr(rArr, gArr, bArr)
 45         rgb = numpy.hstack((rArr.reshape((-1, 1)), gArr.reshape((-1, 1)), bArr.reshape((-1, 1))))
 46         xylv = numpy.hstack((xArr.reshape((-1, 1)), yArr.reshape((-1, 1)), lvArr.reshape((-1, 1))))
 47         return torch.tensor(rgb, dtype=torch.float), torch.tensor(xylv, dtype=torch.float)
 48 
 49     def __generate_xylvArr(self, rArr, gArr, bArr):
 50         xArr = xFunc(rArr, gArr, bArr)
 51         yArr = yFunc(rArr, gArr, bArr)
 52         lvArr = lvFunc(rArr, gArr, bArr)
 53         return xArr, yArr, lvArr
 54 
 55     def __generate_rgbArr(self, num):
 56         rArr = numpy.random.uniform(*self.__rRange, num)
 57         gArr = numpy.random.uniform(*self.__gRange, num)
 58         bArr = numpy.random.uniform(*self.__bRange, num)
 59         return rArr, gArr, bArr
 60 
 61 
 62 # 2. 封装数据
 63 class PackData(object):
 64 
 65     def __init__(self, features, labels, batch_size=None, random_shuffle=True):
 66         self.__features = features
 67         self.__labels = labels
 68         self.__batch_size = batch_size
 69         self.__random_shuffle = random_shuffle
 70 
 71         self.num = self.__features.shape[0]
 72         if self.__batch_size is None:
 73             self.__batch_size = self.num
 74 
 75         self.__indices = list(range(self.num))
 76         if self.__random_shuffle:
 77             numpy.random.shuffle(self.__indices)
 78     
 79     def __call__(self):
 80         for i in range(0, self.num, self.__batch_size):
 81             batchIndices = self.__indices[i:min(i+self.__batch_size, self.num)]
 82             yield self.__features[batchIndices], self.__labels[batchIndices]
 83 
 84 
 85 # 3. 构建模型: multi-layer perceptron
 86 class MLP(object):
 87 
 88     def __init__(self, hidden_dim=100):
 89         self.__hidden_dim = hidden_dim
 90 
 91         self.l1_W = torch.normal(0, 0.01, (3, self.__hidden_dim), requires_grad=True)
 92         self.l1_b = torch.zeros((1, self.__hidden_dim), requires_grad=True)
 93         self.l1_f = torch.nn.Tanh()
 94 
 95         self.l2_W = torch.normal(0, 0.01, (self.__hidden_dim, 3), requires_grad=True)
 96         self.l2_b = torch.zeros((1, 3), requires_grad=True)
 97         
 98     def __call__(self, x):
 99         l1_1 = torch.matmul(x, self.l1_W) + self.l1_b
100         l1_2 = self.l1_f(l1_1)
101 
102         l2_1 = torch.matmul(l1_2, self.l2_W) + self.l2_b
103         return l2_1
104 
105 
106 # 4. 构建损失函数
107 class MSE(object):
108 
109     def __init__(self, lamda):
110         self.__lamda = lamda
111 
112     def __call__(self, Y, Y_, mlpObj=None):
113         L = torch.sum((Y - Y_) ** 2) / 2
114         if mlpObj:
115             term1 = torch.sum(mlpObj.l1_W ** 2)
116             term2 = torch.sum(mlpObj.l2_W ** 2)
117             term3 = (term1 + term2) * self.__lamda / 2
118             L = L + term3
119         return L
120 
121 
122 # 6. 训练单元
123 def training_epoch(packObj, mlpObj, mseObj, optObj):
124     loss_total = 0
125     with torch.enable_grad():
126         for X, Y_ in packObj():
127             optObj.zero_grad()
128             Y = mlpObj(X)
129             loss = mseObj(Y, Y_, mlpObj)
130             loss.backward()
131             optObj.step()
132 
133             loss_total += loss.item()
134     return loss_total
135 
136 
137 # 7. 测试单元
138 def testing_epoch(packObj, mlpObj, mseObj):
139     loss_total = 0
140     with torch.no_grad():
141         for X, Y_ in packObj():
142             Y = mlpObj(X)
143             loss = mseObj(Y, Y_)
144             loss_total += loss.item()
145     return loss_total
146 
147 
148 # 8. 启动训练与测试
149 def train(trainingData, testingData, model, loss, optimizer, maxEpoch=10000):
150     testingLossList = list()
151     for epoch in range(maxEpoch):
152         training_epoch(trainingData, model, loss, optimizer)
153         testingLoss = testing_epoch(testingData, model, loss) / testingData.num
154         testingLossList.append(testingLoss)
155         # if epoch % 100 == 0:
156         #     print("epoch {}: testing error = {:.5f}".format(epoch,
157         #         testingLoss))
158 
159     minIdx = numpy.argmin(testingLossList)
160     testingLossBest = testingLossList[minIdx]
161     return testingLossBest
162 
163 
164 # 9. 模型保存
165 def save(model, filename=None):
166     l1_W = model.l1_W.detach().numpy()
167     l1_b = model.l1_b.detach().numpy()
168     l2_W = model.l2_W.detach().numpy()
169     l2_b = model.l2_b.detach().numpy()
170 
171     if filename is None:
172         filename = "./mlp.dat"
173     with open(filename, "wt") as f:
174         f.write("l1_W = \n")
175         for row in l1_W:
176             for ele in row:
177                 f.write("{:.9f} ".format(ele))
178             f.write("\n")
179         f.write("\nl1_b = \n")
180         for ele in l1_b[0]:
181             f.write("{:.9f} ".format(ele))
182         f.write("\n")
183 
184         f.write("\nl2_W = \n")
185         for row in l2_W:
186             for ele in row:
187                 f.write("{:.9f} ".format(ele))
188             f.write("\n")
189         f.write("\nl2_b = \n")
190         for ele in l2_b[0]:
191             f.write("{:.9f} ".format(ele))
192 
193 
194 # 搜索超参数lamda
195 def search_lamda():
196     rRange = [-10, 10]
197     gRange = [-10, 10]
198     bRange = [-10, 10]
199     trainingNum = 500
200     testingNum = 1000
201     batch_size = 250
202     hidden_dim = 50
203 
204     geneObj = GeneData(rRange, gRange, bRange)
205     trainingData = geneObj.getDataset(trainingNum)
206     testingData = geneObj.getDataset(testingNum)
207     trainingPack = PackData(*trainingData, batch_size)
208     testingPack = PackData(*testingData, batch_size)
209 
210     lamda = 0.001
211     lr = 0.003
212     mlpObj = MLP(hidden_dim)
213     mseObj = MSE(lamda)
214     params = [mlpObj.l1_W, mlpObj.l1_b, mlpObj.l2_W, mlpObj.l2_b]
215     optObj = optim.Adam(params, lr)
216     train(trainingPack, testingPack, mlpObj, mseObj, optObj, 100000)
217     l1_W, l1_b, l2_W, l2_b = mlpObj.l1_W, mlpObj.l1_b, mlpObj.l2_W, mlpObj.l2_b
218 
219     lr = 0.003
220     lamdaList = numpy.linspace(0, 0.01, 101)
221     testList = list()
222     for idx, lamda in enumerate(lamdaList):
223         mlpObj = MLP(hidden_dim)
224         mlpObj.l1_W.requires_grad = False
225         mlpObj.l1_b.requires_grad = False
226         mlpObj.l2_W.requires_grad = False
227         mlpObj.l2_b.requires_grad = False
228         l1_W.requires_grad = False
229         l1_b.requires_grad = False
230         l2_W.requires_grad = False
231         l2_b.requires_grad = False
232         mlpObj.l1_W[:], mlpObj.l1_b[:], mlpObj.l2_W[:], mlpObj.l2_b[:] = l1_W, l1_b, l2_W, l2_b
233         mlpObj.l1_W.requires_grad = True
234         mlpObj.l1_b.requires_grad = True
235         mlpObj.l2_W.requires_grad = True
236         mlpObj.l2_b.requires_grad = True
237         mseObj = MSE(lamda)
238         params = [mlpObj.l1_W, mlpObj.l1_b, mlpObj.l2_W, mlpObj.l2_b]
239         optObj = optim.Adam(params, lr)
240         testingLoss = train(trainingPack, testingPack, mlpObj, mseObj, optObj, 100000)
241         print("lamda = {:5f}, testing error = {}".format(lamda, testingLoss))
242         testList.append(testingLoss)
243         l1_W, l1_b, l2_W, l2_b = mlpObj.l1_W, mlpObj.l1_b, mlpObj.l2_W, mlpObj.l2_b
244 
245     minIdx = numpy.argmin(testList)
246     lamdaBest = lamdaList[minIdx]
247     testBest = testList[minIdx]
248 
249     fig = plt.figure(figsize=(5, 4))
250     ax1 = fig.add_subplot(1, 1, 1)
251     ax1.plot(lamdaList, testList, ".--", lw=1, markersize=5, label="testing error", zorder=1)
252     ax1.scatter(lamdaBest, testBest, marker="*", s=30, c="red", label="optimal", zorder=2)
253     ax1.set(xlabel="$\\lambda$", ylabel="error", title="optimal $\\lambda$ = {:.5f}".format(lamdaBest))
254     ax1.legend()
255     fig.tight_layout()
256     fig.savefig("search_lamda.png", dpi=100)
257 
258     ############
259     maxEpoch = 100000
260     mlpObj = MLP(hidden_dim)
261     mseObj = MSE(lamdaBest)
262     params = [mlpObj.l1_W, mlpObj.l1_b, mlpObj.l2_W, mlpObj.l2_b]
263     optObj = optim.Adam(params, lr)
264 
265     testingLossBest = numpy.inf
266     for epoch in range(maxEpoch):
267         training_epoch(trainingPack, mlpObj, mseObj, optObj)
268         testingLoss = testing_epoch(testingPack, mlpObj, mseObj) / testingPack.num
269         print("epoch {}: testing error best = {}, testing error current = {}".format(epoch, testingLossBest, testingLoss))
270         if testingLoss < testingLossBest:
271             save(mlpObj)
272             testingLossBest = testingLoss
273 
274 
275 
276 if __name__ == "__main__":
277     search_lamda()
    View Code
  • 结果展示
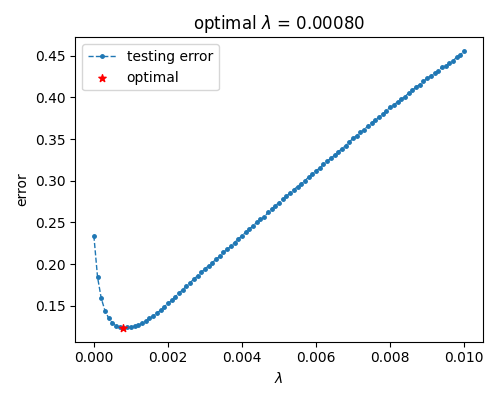    可以看到, 泛化误差在提升权重参数后先下降后上升, 大致对应降低模型复杂度使模型表现从过拟合至欠拟合.
  • 使用建议
    ①. bias代表函数偏置, 直观上对模型复杂度(函数平滑程度)影响微弱, 一般无需正则化;
    ②. 超参数连续调整时, 训练参数迭代初值可选用前一超参数下的收敛值;
    ③. weight decay适用于神经网络所有层.
  • 参考文档
    ①. 动手学深度学习 - 李牧
posted @ 2022-04-29 00:03  LOGAN_XIONG  阅读(155)  评论(0)  编辑  收藏  举报