1 # Poisson's equation之求解 - 有限差分法
2
3 import numpy
4 from matplotlib import pyplot as plt
5
6
7 class PoissonEq(object):
8
9 def __init__(self, nx=150, ny=100, a=3, b=2):
10 self.__nx = nx # x轴子区间划分数
11 self.__ny = ny # y轴子区间划分数
12 self.__Lx = a # x轴椭圆半长
13 self.__Ly = b # y轴椭圆半长
14 self.__epsilon = 1 # 真空介电常数取值
15
16 assert a > b, "a must larger than b"
17
18 self.__hx = 2 * a / nx
19 self.__hy = 2 * b / ny
20 self.__ht = min([self.__hx, self.__hy]) ** 3
21
22 self.__X, self.__Y = self.__build_gridPoints()
23 self.__Ax, self.__Ay = self.__build_2ndOrdMat()
24 self.__V = self.__get_V()
25
26 self.__OuterLoc = self.__X ** 2 / a ** 2 + self.__Y ** 2 / b ** 2 >= 1
27 self.__InnerLoc = self.__X ** 2 / a ** 2 + self.__Y ** 2 / b ** 2 <= 1
28 self.__Angle = numpy.angle(self.__X + 1j * self.__Y)
29
30
31 def get_solu(self, maxIter=1000000, varepsilon=1.e-9):
32 '''
33 数值求解
34 maxIter: 最大迭代次数
35 varepsilon: 收敛判据
36 '''
37 U0 = self.__get_initial_U()
38 self.__fill_boundary_U(U0)
39 for i in range(maxIter):
40 t = i * self.__ht
41 Uk = self.__calc_Uk(t, U0)
42
43 # print(i, numpy.linalg.norm(Uk - U0, numpy.inf))
44 if self.__isConverged(U0, Uk, varepsilon):
45 break
46
47 U0 = Uk
48 else:
49 raise Exception(">>> Not converged after {} iterations!<<<".format(maxIter))
50
51 return numpy.ma.array(self.__X, mask=~self.__InnerLoc), numpy.ma.array(self.__Y, mask=~self.__InnerLoc), numpy.ma.array(Uk, mask=~self.__InnerLoc)
52
53
54 def get_Efield(self, U):
55 '''
56 获取电场
57 '''
58 Ey, Ex = numpy.gradient(U, self.__hy, self.__hx)
59 return numpy.linspace(-self.__Lx, self.__Lx, self.__nx + 1), numpy.linspace(-self.__Ly, self.__Ly, self.__ny + 1), -Ex, -Ey
60
61
62 def __isConverged(self, U0, Uk, varepsilon):
63 normVal = numpy.linalg.norm(Uk - U0, numpy.inf)
64 if normVal < varepsilon:
65 return True
66 return False
67
68
69 def __calc_Uk(self, t, U0):
70 K1 = self.__calc_F(U0)
71 Uk = U0 + K1 * self.__ht
72 self.__fill_boundary_U(Uk)
73 return Uk
74
75
76 def __calc_F(self, U):
77 term0 = numpy.matmul(U, self.__Ax) / self.__hx ** 2
78 term1 = numpy.matmul(self.__Ay, U) / self.__hy ** 2
79 term2 = self.__V / self.__epsilon
80 FVal = term0 + term1 + term2
81 return FVal
82
83
84 def __fill_boundary_U(self, U):
85 '''
86 填充边界条件
87 '''
88 U[self.__OuterLoc] = numpy.cos(self.__Angle[self.__OuterLoc])
89
90
91 def __get_initial_U(self):
92 '''
93 获取初始条件
94 '''
95 U0 = numpy.zeros(self.__X.shape)
96 return U0
97
98
99 def __get_V(self):
100 '''
101 获取电荷密度
102 '''
103 c = numpy.math.sqrt(self.__Lx ** 2 - self.__Ly ** 2)
104 term0 = -100 * ((self.__X - c) ** 2 + self.__Y ** 2)
105 term1 = -100 * ((self.__X + c) ** 2 + self.__Y ** 2)
106 V = 100 * numpy.exp(term0) - 100 * numpy.exp(term1)
107 return V
108
109
110 def __build_2ndOrdMat(self):
111 '''
112 构造2阶微分算子的矩阵形式
113 '''
114 Ax = self.__build_AMat(self.__nx + 1)
115 Ay = self.__build_AMat(self.__ny + 1)
116 return Ax, Ay
117
118
119 def __build_AMat(self, n):
120 term0 = numpy.identity(n) * -2
121 term1 = numpy.eye(n, n, 1)
122 term2 = numpy.eye(n, n, -1)
123 AMat = term0 + term1 + term2
124 return AMat
125
126
127 def __build_gridPoints(self):
128 '''
129 构造网格节点
130 '''
131 X = numpy.linspace(-self.__Lx, self.__Lx, self.__nx + 1)
132 Y = numpy.linspace(-self.__Ly, self.__Ly, self.__ny + 1)
133 X, Y = numpy.meshgrid(X, Y)
134 return X, Y
135
136
137 class PoissonPlot(object):
138
139 @staticmethod
140 def plot_fig(poiObj):
141 maxIter = 1000000
142 varepsilon = 1.e-9
143
144 X, Y, U = poiObj.get_solu(maxIter, varepsilon)
145 X1, Y1, Ex, Ey = poiObj.get_Efield(U)
146
147 fig = plt.figure(figsize=(6, 4))
148 ax1 = plt.subplot()
149
150 cs1 = ax1.contour(X, Y, U, levels=50, cmap="jet")
151 ax1.streamplot(X1, Y1, Ex, Ey, density=1, linewidth=1, color="black")
152 fig.colorbar(cs1)
153 fig.tight_layout()
154 fig.savefig("plot_fig.png", dpi=100)
155
156
157 if __name__ == "__main__":
158 nx = 150
159 ny = 100
160 a = 1.5
161 b = 1
162 poiObj = PoissonEq(nx, ny, a, b)
163
164 PoissonPlot.plot_fig(poiObj)
View Code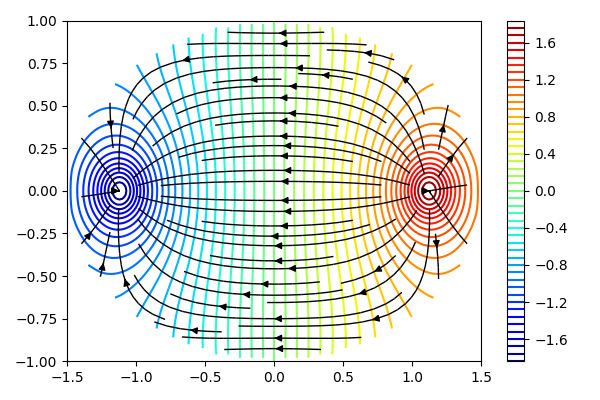
注意, 图中等高线代表等势线, 流线代表电场走向.
