Smooth Support Vector Regression - Python实现

• 算法特征:
  ①. 所有点尽可能落在管道内; ②. 极大化margin; ③. 极小化管道残差.
• 算法推导:
  Part Ⅰ
  引入光滑化手段: 详见https://www.cnblogs.com/xxhbdk/p/12275567.html
  定义:
  \begin{equation*}
  \begin{split}
  \left| x \right|_{\epsilon} &= \max\{0, \left| x \right| - \epsilon\} \\
  &=\max\{0, x - \epsilon\} + \max\{0, -x - \epsilon\} \\
  &=(x-\epsilon)_+ + (-x-\epsilon)_+
  \end{split}
  \end{equation*}
  由于$(x-\epsilon)_+ \cdot (-x-\epsilon)_+ = 0$, 则
  \begin{equation*}
  \left|x\right|_{\epsilon}^2 = (x-\epsilon)_+^2 + (-x - \epsilon)_+^2
  \end{equation*}
  定义:
  \begin{equation*}
  p_{\epsilon}^2(x, \beta) = (p(x-\epsilon, \beta))^2 + (p(-x-\epsilon, \beta))^2
  \end{equation*}
  其中, $p(x, \beta) =  \frac{1}{\beta}\ln(\mathrm{e}^{\beta x} + 1)$, $\beta$为光滑化参数.
  现采用$p_{\epsilon}^2(x, \beta)$近似$\left|x\right|_{\epsilon}^2$, 相关函数图像如下:
  下面给出$p_{\epsilon}^2(x, \beta)$的1阶及2阶导数:
  \begin{align*}
  \frac{\mathrm{d}p_{\epsilon}^2(x, \beta)}{\mathrm{d}x} &= 2[p(x-\epsilon, \beta)s(x-\epsilon, \beta) - p(-x-\epsilon, \beta)s(-x-\epsilon, \beta)]  \\
  \frac{\mathrm{d}^2p_{\epsilon}^2(x, \beta)}{\mathrm{d}x^2} &= 2[s^2(x-\epsilon, \beta) + p(x-\epsilon, \beta)\delta(x-\epsilon, \beta) + s^2(-x-\epsilon, \beta) + p(-x-\epsilon, \beta)\delta(-x-\epsilon, \beta)]
  \end{align*}
  其中, $s(x, \beta) = 1 / (\mathrm{e}^{-\beta x} + 1)$, $\delta(x, \beta) = \beta \mathrm{e}^{\beta x} / (\mathrm{e}^{\beta x} + 1)^2$.
  
  Part Ⅱ
  SVR线性回归方程如下:
  \begin{equation}
  h(x) = W^\mathrm{T}x + b
  \label{eq_1}
  \end{equation}
  其中, $W$是超平面法向量, $b$是超平面偏置参数.
  本文拟采用$L_2$范数衡量拟合残差, 则SVR原始优化问题如下:
  \begin{equation}
  \begin{split}
  \min\quad &\frac{1}{2}\|W\|_2^2 + \frac{c}{2}(\|\xi\|_2^2 + \|\xi^{\ast}\|_2^2) \\
  \mathrm{s.t.}\quad & \bar{Y} - (A^{\mathrm{T}}W + \mathbf{1}b) \leq \mathbf{1}\epsilon + \xi \\
  & \bar{Y} - (A^{\mathrm{T}}W + \mathbf{1}b) \geq -\mathbf{1}\epsilon - \xi^{\ast}
  \end{split}
  \label{eq_2}
  \end{equation}
  其中, $A = [x^{(1)}, x^{(2)}, \cdots, x^{(n)}]$, $\bar{Y} = [\bar{y}^{(1)}, \bar{y}^{(2)}, \cdots, \bar{y}^{(n)}]^{\mathrm{T}}$, $\epsilon$是管道残差参数, $\xi$是由所有样本上管道残差组成的列矢量, $-\xi^{\ast}$是由所有样本下管道残差组成的列矢量, $c$为权重参数.
  根据上述优化问题(\ref{eq_2}), 管道残差$\xi$、$\xi^{\ast}$可采用plus function等效表示:
  \begin{equation}
  \begin{cases}
  \xi = (\bar{Y} - (A^{\mathrm{T}}W + \mathbf{1}b) - \mathbf{1}\epsilon)_+   \\
  \xi^{\ast} = (- \bar{Y} + (A^{\mathrm{T}}W + \mathbf{1}b) - \mathbf{1}\epsilon)_+
  \end{cases}
  \label{eq_3}
  \end{equation}
  由此可将该有约束最优化问题转化为如下无约束最优化问题:
  \begin{equation}
  \min\quad \frac{1}{2}\|W\|_2^2 + \frac{c}{2}(\| (\bar{Y} - (A^{\mathrm{T}}W + \mathbf{1}b) - \mathbf{1}\epsilon)_+ \|_2^2 + \| (- \bar{Y} + (A^{\mathrm{T}}W + \mathbf{1}b) - \mathbf{1}\epsilon)_+ \|_2^2)
  \label{eq_4}
  \end{equation}
  同样, 根据优化问题(\ref{eq_2})KKT条件中关于原变量$W$的稳定性条件有:
  \begin{equation}
  W = A(\alpha - \alpha^{\ast}) = A\alpha^{\prime}
  \label{eq_5}
  \end{equation}
  其中, $\alpha$、$\alpha^{\ast}$均为对偶变量. 代入式(\ref{eq_4})变数变换可得:
  \begin{equation}
  \min\quad \frac{1}{2}\alpha^{\prime\mathrm{T}}A^{\mathrm{T}}A\alpha^{\prime} + \frac{c}{2}(\| (\bar{Y} - (A^{\mathrm{T}}A\alpha^{\prime} + \mathbf{1}b) - \mathbf{1}\epsilon)_+ \|_2^2 + \| (- \bar{Y} + (A^{\mathrm{T}}A\alpha^{\prime} + \mathbf{1}b) - \mathbf{1}\epsilon)_+ \|_2^2)
  \label{eq_6}
  \end{equation}
  由于权重参数$c$的存在, 上述最优化问题等效如下多目标最优化问题:
  \begin{equation}
  \left\{
  \begin{split}
  &\min\quad \frac{1}{2}\alpha^{\prime\mathrm{T}}A^{\mathrm{T}}A\alpha^{\prime}   \\
  &\min\quad \frac{1}{2}(\| (\bar{Y} - (A^{\mathrm{T}}A\alpha^{\prime} + \mathbf{1}b) - \mathbf{1}\epsilon)_+ \|_2^2 + \| (- \bar{Y} + (A^{\mathrm{T}}A\alpha^{\prime} + \mathbf{1}b) - \mathbf{1}\epsilon)_+ \|_2^2)
  \end{split}
  \right.
  \label{eq_7}
  \end{equation}
  由于$A^{\mathrm{T}}A\succeq 0$, 有如下等效:
  \begin{equation}
  \min\quad \frac{1}{2}\alpha^{\prime\mathrm{T}}A^{\mathrm{T}}A\alpha^{\prime} \quad\Rightarrow\quad \min\quad \frac{1}{2}\alpha^{\prime\mathrm{T}}\alpha^{\prime}
  \label{eq_8}
  \end{equation}
  根据Part Ⅰ中光滑化手段, 有如下等效:
  \begin{equation}
  \min\quad \frac{1}{2}(\| (\bar{Y} - (A^{\mathrm{T}}A\alpha^{\prime} + \mathbf{1}b) - \mathbf{1}\epsilon)_+ \|_2^2 + \| (- \bar{Y} + (A^{\mathrm{T}}A\alpha^{\prime} + \mathbf{1}b) - \mathbf{1}\epsilon)_+ \|_2^2) \quad\Rightarrow\quad \min\quad \frac{1}{2}\sum_ip_{\epsilon}^2(\bar{y}^{(i)} - x^{(i)\mathrm{T}}A\alpha^{\prime} - b, \beta), \quad \text{where } \beta\rightarrow\infty
  \label{eq_9}
  \end{equation}
  结合式(\ref{eq_8})、式(\ref{eq_9}), 优化问题(\ref{eq_6})等效如下:
  \begin{equation}
  \min\quad \frac{1}{2}\alpha^{\prime\mathrm{T}}\alpha^{\prime} + \frac{c}{2}\sum_ip_{\epsilon}^2(\bar{y}^{(i)} - x^{(i)\mathrm{T}}A\alpha^{\prime} - b, \beta), \quad \text{where } \beta\rightarrow\infty
  \label{eq_10}
  \end{equation}
  为增强模型的回归能力, 引入kernel trick, 得最终优化问题:
  \begin{equation}
  \min\quad \frac{1}{2}\alpha^{\prime\mathrm{T}}\alpha^{\prime} + \frac{c}{2}\sum_ip_{\epsilon}^2(\bar{y}^{(i)} - K(x^{(i)\mathrm{T}}, A)\alpha^{\prime} - b, \beta), \quad \text{where } \beta\rightarrow\infty
  \label{eq_11}
  \end{equation}
  其中, $K$代表kernel矩阵. 内部元素$K_{ij}=k(x^{(i)}, x^{(j)})$由kernel函数决定. 常见的kernel函数如下:
  ①. 多项式核: $k(x^{(i)}, x^{(j)}) = (x^{(i)}\cdot x^{(j)})^n$
  ②. 高斯核: $k(x^{(i)}, x^{(j)}) = \mathrm{e}^{-\mu\|x^{(i)} - x^{(j)}\|_2^2}$
  结合式(\ref{eq_1})、式(\ref{eq_5})及kernel trick可得最终回归方程:
  \begin{equation}
  h(x) = \alpha^{\prime\mathrm{T}}K(A^{\mathrm{T}}, x) + b
  \label{eq_12}
  \end{equation}
  
  Part Ⅲ
  以下给出优化相关协助信息, 拟设式(\ref{eq_11})之目标函数为$J$, 并令:
  \begin{equation}
  J = J_1 + J_2 \quad\quad\text{其中,}
  \left\{\begin{split}
  &J_1 =  \frac{1}{2}\alpha^{\prime\mathrm{T}}\alpha^{\prime}   \\
  &J_2 = \frac{c}{2}\sum\limits_ip_{\epsilon}^2(\bar{y}^{(i)} - K(x^{(i)\mathrm{T}}, A)\alpha^{\prime} - b, \beta)
  \end{split}
  \right.
  \label{eq_13}
  \end{equation}
  $J_1$相关:
  \begin{gather*}
  \frac{\partial J_1}{\partial \alpha^{\prime}} = \alpha^{\prime} \quad
  \frac{\partial J_1}{\partial b} = 0   \\
  \frac{\partial^2 J_1}{\partial \alpha^{\prime 2}} = I \quad
  \frac{\partial^2 J_1}{\partial \alpha^{\prime} \partial b} = 0 \quad
  \frac{\partial^2 J_1}{\partial b \partial \alpha^{\prime}} = 0 \quad
  \frac{\partial^2 J_1}{\partial b^2} = 0
  \end{gather*}
  \begin{gather*}
  \nabla J_1 = \begin{bmatrix}\frac{\partial J_1}{\partial \alpha^{\prime}} \\ \frac{\partial J_1}{\partial b} \end{bmatrix}   \\ \\
  \nabla^2 J_1 = \begin{bmatrix} \frac{\partial^2 J_1}{\partial \alpha^{\prime 2}} & \frac{\partial^2 J_1}{\partial \alpha^{\prime} \partial b} \\  \frac{\partial^2 J_1}{\partial b \partial \alpha^{\prime}} & \frac{\partial^2 J_1}{\partial b^2} \end{bmatrix}
  \end{gather*}
  $J_2$相关:
  \begin{gather*}
  z_i = \bar{y}^{(i)} - K(x^{(i)\mathrm{T}}, A)\alpha^{\prime} - b   \\
  \frac{\partial J_2}{\partial \alpha^{\prime}} = -c\sum_i[p(z_i-\epsilon, \beta)s(z_i-\epsilon, \beta) - p(-z_i - \epsilon, \beta)s(-z_i-\epsilon, \beta)]K^{\mathrm{T}}(x^{(i)\mathrm{T}}, A)   \\
  \frac{\partial J_2}{\partial b} = -c\sum_i[p(z_i-\epsilon, \beta)s(z_i-\epsilon, \beta) - p(-z_i - \epsilon, \beta)s(-z_i - \epsilon, \beta)]   \\
  \frac{\partial^2 J_2}{\partial \alpha^{\prime 2}} = c\sum_i[s^2(z_i-\epsilon, \beta) + p(z_i-\epsilon, \beta)\delta(z_i-\epsilon, \beta) + s^2(-z_i-\epsilon, \beta) + p(-z_i-\epsilon, \beta)\delta(-z_i-\epsilon, \beta)]K^{\mathrm{T}}(x^{(i)\mathrm{T}}, A)K(x^{(i)\mathrm{T}}, A)   \\
  \frac{\partial^2 J_2}{\partial \alpha^{\prime} \partial b} = c\sum_i[s^2(z_i-\epsilon, \beta) + p(z_i-\epsilon, \beta)\delta(z_i-\epsilon, \beta) + s^2(-z_i-\epsilon, \beta) + p(-z_i-\epsilon, \beta)\delta(-z_i-\epsilon, \beta)]K^{\mathrm{T}}(x^{(i)\mathrm{T}}, A)   \\
  \frac{\partial^2 J_2}{\partial b \partial \alpha^{\prime}} = c\sum_i[s^2(z_i-\epsilon, \beta) + p(z_i-\epsilon, \beta)\delta(z_i-\epsilon, \beta) + s^2(-z_i-\epsilon, \beta) + p(-z_i-\epsilon, \beta)\delta(-z_i-\epsilon, \beta)]K(x^{(i)\mathrm{T}}, A)   \\
  \frac{\partial^2 J_2}{\partial b^2} = c\sum_i[s^2(z_i-\epsilon, \beta) + p(z_i-\epsilon, \beta)\delta(z_i-\epsilon, \beta) + s^2(-z_i-\epsilon, \beta) + p(-z_i-\epsilon, \beta)\delta(-z_i-\epsilon, \beta)]
  \end{gather*}
  \begin{gather*}
  \nabla J_2 = \begin{bmatrix}\frac{\partial J_2}{\partial \alpha^{\prime}} \\ \frac{\partial J_2}{\partial b} \end{bmatrix}   \\ \\
  \nabla^2 J_2 = \begin{bmatrix} \frac{\partial^2 J_2}{\partial \alpha^{\prime 2}} & \frac{\partial^2 J_2}{\partial \alpha^{\prime} \partial b} \\  \frac{\partial^2 J_2}{\partial b \partial \alpha^{\prime}}& \frac{\partial^2 J_2}{\partial b^2} \end{bmatrix}
  \end{gather*}
  目标函数$J$之gradient及Hessian如下:
  \begin{align}
  \nabla J &= \nabla J_1 + \nabla J_2   \\
  \nabla^2 J &= \nabla^2 J_1 + \nabla^2 J_2
  \end{align}
  
  Part Ⅳ
  现以如下peaks function为例进行算法实施:
  \begin{equation*}
  f(x_1, x_2) = 3(1 - x_1)^2\mathrm{e}^{-x_1^2 - (x_2 + 1)^2} - 10(\frac{x_1}{5} - x_1^3 - x_2^5)\mathrm{e}^{-x_1^2 - x_2^2} - \frac{1}{3}\mathrm{e}^{-(x_1 + 1)^2 - x_2^2}, \quad \text{where } x_1\in[-3, 3], x_2\in[-3, 3]
  \end{equation*}
  标准函数图像如下:
  
  
  
  
  
  
• 代码实现:
  

  # Smooth Support Vector Regression之实现
  
  import numpy
  from matplotlib import pyplot as plt
  from mpl_toolkits.mplot3d import Axes3D
  
  
  numpy.random.seed(0)
  
  def peaks(x1, x2):
      term1 = 3 * (1 - x1) ** 2 * numpy.exp(-x1 ** 2 - (x2 + 1) ** 2)
      term2 = -10 * (x1 / 5 - x1 ** 3 - x2 ** 5) * numpy.exp(-x1 ** 2 - x2 ** 2)
      term3 = -numpy.exp(-(x1 + 1) ** 2 - x2 ** 2) / 3
      val = term1 + term2 + term3
      return val
      
  
  # 生成回归数据
  X1 = numpy.linspace(-3, 3, 30)
  X2 = numpy.linspace(-3, 3, 30)
  X1, X2 = numpy.meshgrid(X1, X2)
  X = numpy.hstack((X1.reshape((-1, 1)), X2.reshape((-1, 1))))     # 待回归数据之样本点
  Y = peaks(X1, X2).reshape((-1, 1))
  Yerr = Y + numpy.random.normal(0, 0.4, size=Y.shape)             # 待回归数据之观测值
  
  
  
  class SSVR(object):
      
      def __init__(self, X, Y_, c=50, mu=1, epsilon=0.5, beta=10):
          '''
          X: 样本点数据集, 1行代表1个样本
          Y_: 观测值数据集, 1行代表1个观测值
          '''
          self.__X = X                                             # 待回归数据之样本点
          self.__Y_ = Y_                                           # 待回归数据之观测值
          self.__c = c                                             # 误差项权重参数
          self.__mu = mu                                           # gaussian kernel参数
          self.__epsilon = epsilon                                 # 管道残差参数
          self.__beta = beta                                       # 光滑化参数
          
          self.__A = X.T
          
      
      def get_estimation(self, x, alpha, b):
          '''
          获取估计值
          '''
          A = self.__A
          mu = self.__mu
          
          x = numpy.array(x).reshape((-1, 1))
          KAx = self.__get_KAx(A, x, mu)
          regVal = self.__calc_hVal(KAx, alpha, b)
          return regVal
          
          
      def get_MAE(self, alpha, b):
          '''
          获取平均绝对误差
          '''
          X = self.__X
          Y_ = self.__Y_
          
          Y = numpy.array(list(self.get_estimation(x, alpha, b) for x in X)).reshape((-1, 1))
          RES = Y_ - Y
          MAE = numpy.linalg.norm(RES, ord=1) / alpha.shape[0]
          return MAE
          
          
      def get_GE(self):
          '''
          获取泛化误差
          '''
          X = self.__X
          Y_ = self.__Y_
          
          cnt = 0
          GE = 0
          for idx in range(X.shape[0]):
              x = X[idx:idx+1, :]
              y_ = Y_[idx, 0]
              
              self.__X = numpy.vstack((X[:idx, :], X[idx+1:, :]))
              self.__Y_ = numpy.vstack((Y_[:idx, :], Y_[idx+1:, :]))
              self.__A = self.__X.T
              alpha, b, tab = self.optimize()
              if not tab:
                  continue
              cnt += 1
              y = self.get_estimation(x, alpha, b)
              GE += (y_ - y) ** 2
          GE /= cnt
          
          self.__X = X
          self.__Y_ = Y_
          self.__A = X.T
          return GE
          
      
      def optimize(self, maxIter=1000, EPSILON=1.e-9):
          '''
          maxIter: 最大迭代次数
          EPSILON: 收敛判据, 梯度趋于0则收敛
          '''
          A, Y_ = self.__A, self.__Y_
          c = self.__c
          mu = self.__mu
          epsilon = self.__epsilon
          beta = self.__beta
          
          alpha, b = self.__init_alpha_b((A.shape[1], 1))
          KAA = self.__get_KAA(A, mu)
          JVal = self.__calc_JVal(KAA, Y_, c, epsilon, beta, alpha, b)
          grad = self.__calc_grad(KAA, Y_, c, epsilon, beta, alpha, b)
          Hess = self.__calc_Hess(KAA, Y_, c, epsilon, beta, alpha, b)
          
          for i in range(maxIter):
              print("iterCnt: {:3d},   JVal: {}".format(i, JVal))
              if self.__converged1(grad, EPSILON):
                  return alpha, b, True
                  
              dCurr = -numpy.matmul(numpy.linalg.inv(Hess), grad)
              ALPHA = self.__calc_ALPHA_by_ArmijoRule(alpha, b, JVal, grad, dCurr, KAA, Y_, c, epsilon, beta)
              
              delta = ALPHA * dCurr
              alphaNew = alpha + delta[:-1, :]
              bNew = b + delta[-1, -1]
              JValNew = self.__calc_JVal(KAA, Y_, c, epsilon, beta, alphaNew, bNew)
              if self.__converged2(delta, JValNew - JVal, EPSILON):
                  return alphaNew, bNew, True
              
              alpha, b, JVal = alphaNew, bNew, JValNew
              grad = self.__calc_grad(KAA, Y_, c, epsilon, beta, alpha, b)
              Hess = self.__calc_Hess(KAA, Y_, c, epsilon, beta, alpha, b)
          else:
              if self.__converged1(grad, EPSILON):
                  return alpha, b, True
          return alpha, b, False
              
              
      def __converged2(self, delta, JValDelta, EPSILON):
          val1 = numpy.linalg.norm(delta)
          val2 = numpy.linalg.norm(JValDelta)
          if val1 <= EPSILON or val2 <= EPSILON:
              return True
          return False
      
      
      def __calc_ALPHA_by_ArmijoRule(self, alphaCurr, bCurr, JCurr, gCurr, dCurr, KAA, Y_, c, epsilon, beta, C=1.e-4, v=0.5):
          i = 0
          ALPHA = v ** i
          delta = ALPHA * dCurr
          alphaNext = alphaCurr + delta[:-1, :]
          bNext = bCurr + delta[-1, -1]
          JNext = self.__calc_JVal(KAA, Y_, c, epsilon, beta, alphaNext, bNext)
          while True:
              if JNext <= JCurr + C * ALPHA * numpy.matmul(dCurr.T, gCurr)[0, 0]: break
              i += 1
              ALPHA = v ** i
              delta = ALPHA * dCurr
              alphaNext = alphaCurr + delta[:-1, :]
              bNext = bCurr + delta[-1, -1]
              JNext = self.__calc_JVal(KAA, Y_, c, epsilon, beta, alphaNext, bNext)
          return ALPHA
                  
                  
      def __converged1(self, grad, EPSILON):
          if numpy.linalg.norm(grad) <= EPSILON:
              return True
          return False
          
          
      def __calc_Hess(self, KAA, Y_, c, epsilon, beta, alpha, b):
          Hess_J1 = self.__calc_Hess_J1(alpha)
          Hess_J2 = self.__calc_Hess_J2(KAA, Y_, c, epsilon, beta, alpha, b)
          Hess = Hess_J1 + Hess_J2
          return Hess
          
          
      def __calc_Hess_J2(self, KAA, Y_, c, epsilon, beta, alpha, b):
          Hess_J2_alpha_alpha = numpy.zeros((KAA.shape[0], KAA.shape[0]))
          Hess_J2_alpha_b = numpy.zeros((KAA.shape[0], 1))
          Hess_J2_b_alpha = numpy.zeros((1, KAA.shape[0]))
          Hess_J2_b_b = 0
          
          z = Y_ - numpy.matmul(KAA, alpha) - b
          term1 = z - epsilon
          term2 = -z - epsilon
          for i in range(z.shape[0]):
              term3 = self.__s(term1[i, 0], beta) ** 2 + self.__p(term1[i, 0], beta) * self.__d(term1[i, 0], beta)
              term4 = self.__s(term2[i, 0], beta) ** 2 + self.__p(term2[i, 0], beta) * self.__d(term2[i, 0], beta)
              term5 = term3 + term4
              Hess_J2_alpha_alpha += term5 * numpy.matmul(KAA[:, i:i+1], KAA[i:i+1, :])
              Hess_J2_alpha_b += term5 * KAA[:, i:i+1]
              Hess_J2_b_b += term5
          Hess_J2_alpha_alpha *= c
          Hess_J2_alpha_b *= c
          Hess_J2_b_alpha = Hess_J2_alpha_b.reshape((1, -1))
          Hess_J2_b_b *= c
  
          Hess_J2_upper = numpy.hstack((Hess_J2_alpha_alpha, Hess_J2_alpha_b))
          Hess_J2_lower = numpy.hstack((Hess_J2_b_alpha, [[Hess_J2_b_b]]))
          Hess_J2 = numpy.vstack((Hess_J2_upper, Hess_J2_lower))
          return Hess_J2
          
          
      def __calc_Hess_J1(self, alpha):
          I = numpy.identity(alpha.shape[0])
          term = numpy.hstack((I, numpy.zeros((I.shape[0], 1))))
          Hess_J1 = numpy.vstack((term, numpy.zeros((1, term.shape[1]))))
          return Hess_J1
          
          
      def __calc_grad(self, KAA, Y_, c, epsilon, beta, alpha, b):
          grad_J1 = self.__calc_grad_J1(alpha)
          grad_J2 = self.__calc_grad_J2(KAA, Y_, c, epsilon, beta, alpha, b)
          grad = grad_J1 + grad_J2
          return grad
          
          
      def __calc_grad_J2(self, KAA, Y_, c, epsilon, beta, alpha, b):
          grad_J2_alpha = numpy.zeros((KAA.shape[0], 1))
          grad_J2_b = 0
          
          z = Y_ - numpy.matmul(KAA, alpha) - b
          term1 = z - epsilon
          term2 = -z - epsilon
          for i in range(z.shape[0]):
              term3 = self.__p(term1[i, 0], beta) * self.__s(term1[i, 0], beta) - self.__p(term2[i, 0], beta) * self.__s(term2[i, 0], beta)
              grad_J2_alpha += term3 * KAA[:, i:i+1]
              grad_J2_b += term3
          grad_J2_alpha *= -c
          grad_J2_b *= -c
  
          grad_J2 = numpy.vstack((grad_J2_alpha, [[grad_J2_b]]))
          return grad_J2
          
          
      def __calc_grad_J1(self, alpha):
          grad_J1 = numpy.vstack((alpha, [[0]]))
          return grad_J1
          
      
      def __calc_JVal(self, KAA, Y_, c, epsilon, beta, alpha, b):
          J1 = self.__calc_J1(alpha)
          J2 = self.__calc_J2(KAA, Y_, c, epsilon, beta, alpha, b)
          JVal = J1 + J2
          return JVal
          
      
      def __calc_J2(self, KAA, Y_, c, epsilon, beta, alpha, b):
          z = Y_ - numpy.matmul(KAA, alpha) - b
          term2 = numpy.sum(self.__p_epsilon_square(item[0], epsilon, beta) for item in z)
          J2 = term2 * c / 2
          return J2
      
          
      def __calc_J1(self, alpha):
          J1 = numpy.sum(alpha * alpha) / 2
          return J1
          
          
      def __p(self, x, beta):
          val = numpy.log(numpy.exp(beta * x) + 1) / beta
          return val
          
          
      def __s(self, x, beta):
          val = 1 / (numpy.exp(-beta * x) + 1)
          return val
          
          
      def __d(self, x, beta):
          term = numpy.exp(beta * x)
          val = beta * term / (term + 1) ** 2
          return val
          
          
      def __p_epsilon_square(self, x, epsilon, beta):
          term1 = self.__p(x - epsilon, beta) ** 2
          term2 = self.__p(-x - epsilon, beta) ** 2
          val = term1 + term2
          return val
          
      
      def __get_KAA(self, A, mu):
          KAA = numpy.zeros((A.shape[1], A.shape[1]))
          for rowIdx in range(KAA.shape[0]):
              for colIdx in range(rowIdx + 1):
                  x1 = A[:, rowIdx:rowIdx+1]
                  x2 = A[:, colIdx:colIdx+1]
                  val = self.__calc_gaussian(x1, x2, mu)
                  KAA[rowIdx, colIdx] = KAA[colIdx, rowIdx] = val
          return KAA
      
      
      def __calc_gaussian(self, x1, x2, mu):
          val = numpy.exp(-mu * numpy.linalg.norm(x1 - x2) ** 2)
          # val = numpy.sum(x1 * x2)
          return val
          
          
      def __init_alpha_b(self, shape):
          '''
          alpha、b之初始化
          '''
          alpha, b = numpy.zeros(shape), 0
          return alpha, b
          
          
      def __calc_hVal(self, KAx, alpha, b):
          hVal = numpy.matmul(alpha.T, KAx)[0, 0] + b
          return hVal
      
      
      def __get_KAx(self, A, x, mu):
          KAx = numpy.zeros((A.shape[1], 1))
          for rowIdx in range(KAx.shape[0]):
              x1 = A[:, rowIdx:rowIdx+1]
              val = self.__calc_gaussian(x1, x, mu)
              KAx[rowIdx, 0] = val
          return KAx
          
          
          
  class PeaksPlot(object):
      
      def peaks_plot(self, X, Y_, ssvrObj, alpha, b):
          surfX1 = numpy.linspace(numpy.min(X[:, 0]), numpy.max(X[:, 0]), 50)
          surfX2 = numpy.linspace(numpy.min(X[:, 1]), numpy.max(X[:, 1]), 50)
          surfX1, surfX2 = numpy.meshgrid(surfX1, surfX2)
          surfY_ = peaks(surfX1, surfX2)
          
          surfY = numpy.zeros(surfX1.shape)
          for rowIdx in range(surfY.shape[0]):
              for colIdx in range(surfY.shape[1]):
                  surfY[rowIdx, colIdx] = ssvrObj.get_estimation((surfX1[rowIdx, colIdx], surfX2[rowIdx, colIdx]), alpha, b)
          
          fig = plt.figure(figsize=(10, 3))
          ax1 = plt.subplot(1, 2, 1, projection="3d")
          ax2 = plt.subplot(1, 2, 2, projection="3d")
          
          norm = plt.Normalize(surfY_.min(), surfY_.max())
          colors = plt.cm.rainbow(norm(surfY_))
          surf = ax1.plot_surface(surfX1, surfX2, surfY_, facecolors=colors, shade=True, alpha=0.5)
          surf.set_facecolor("white")
          ax1.scatter3D(X[:, 0:1], X[:, 1:2], Y_, s=1, c="r")
          ax1.set(xlabel="$x_1$", ylabel="$x_2$", zlabel="$f(x_1, x_2)$", xlim=(-3, 3), ylim=(-3, 3), zlim=(-8, 8))
          ax1.set(title="Original Function")
          ax1.view_init(0, 0)
          
          norm2 = plt.Normalize(surfY.min(), surfY.max())
          colors2 = plt.cm.rainbow(norm2(surfY))
          surf2 = ax2.plot_surface(surfX1, surfX2, surfY, facecolors=colors2, shade=True, alpha=0.5)
          surf2.set_facecolor("white")
          ax2.scatter3D(X[:, 0:1], X[:, 1:2], Y_, s=1, c="r")
          ax2.set(xlabel="$x_1$", ylabel="$x_2$", zlabel="$f(x_1, x_2)$", xlim=(-3, 3), ylim=(-3, 3), zlim=(-8, 8))
          ax2.set(title="Estimated Function")
          ax2.view_init(0, 0)
          
          fig.tight_layout()
          fig.savefig("peaks_plot.png", dpi=100)
          
          
          
  if __name__ == "__main__":
      ssvrObj = SSVR(X, Yerr, c=50, mu=1, epsilon=0.5)
      alpha, b, tab = ssvrObj.optimize()
      
      ppObj = PeaksPlot()
      ppObj.peaks_plot(X, Yerr, ssvrObj, alpha, b)

• 结果展示:
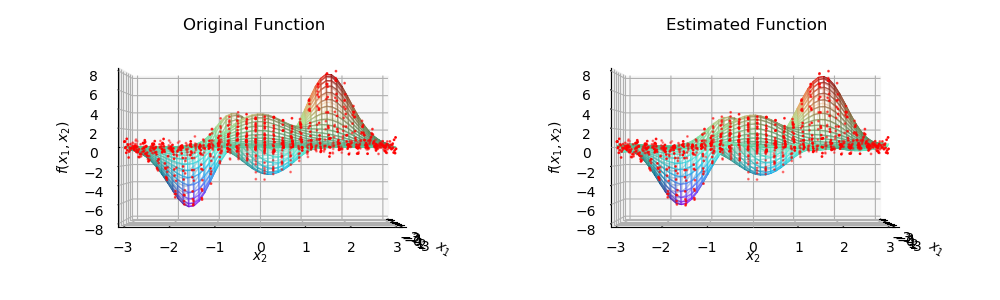  左侧为样本点分布及原始函数图像, 右侧为样本点分布及估计函数图像.
• 使用建议:
  ①. 极大化margin可使管道投影加粗, 进一步使回归样本点尽可能落在管道投影内部;
  ②. SSVR本质上求解的仍然是原问题, 此时$\alpha^{\prime}$仅作为变数变换引入, 无需满足KKT条件中对偶可行性;
  ③. 数据集是否需要归一化, 应按实际情况予以考虑.
• 参考文档:
  Yuh-Jye Lee, Wen-Feng Hsieh, and Chien-Ming Huang. "$\epsilon$-SSVR: A Smooth Support Vector Machine for $\epsilon$-Insensitive Regression", IEEE Transactions on Knowledge and Data Engineering, VoL. 17, No. 5, (2005), 678-685.