考研线性代数
行列式
行列式就是一个数或者一个式子
定义
- 逆序: 若\(i<j - (i,j)\)称为正序,若\(i>j - (i,j)\)称为逆序
- 逆序数:一个排列里面包括的逆序的总个数
- n阶行列式:n阶行列式等于所有取自不同行不同列的n个元素的乘积的代数和,逆序数为偶数时带正号,逆序数为奇数时带负号,共有n!项
- 余子式:行列式划去该元素所在的行与列的各元素,剩下的元素按原样排列,得到的新行列式
- 代数余子式:行列式某元素的余子式与该元素对应的正负符号的乘积
- \(A_{ij}=(-1)^{(i+j)}M_{ij}\) 其中 \(A_{ij}\)为代数余子式,\(M_{ij}\)为余子式

易算行列式
- 对角行列式:上三角,下三角,对角都为主对角线乘积
- 范德蒙行列式
\[V_n=
\left[
\begin{matrix}
1 & 1 & \cdots & 1 \\
a_1 & a_2 & \cdots & a_n \\
a^2_1 & a^2_2 & \cdots & a^2_n \\
\vdots & \vdots & \ddots & \vdots \\
a^{n-1}_1 & a^{n-1}_2 & \cdots & a^{n-1}_n \\
\end{matrix}
\right]=\prod_{1\leq j<i\leq n}(a_i-a_j)
\]
\(V_n!=0\) 充分必要 \(a_1,a_2,a_3 \cdots a_n\)两两不等
计算性质
- 行列式与其转化行列式相等,即\(D=D^T\)
- 对调两行或者两列改变符号
- 行列式某行(或列)有公因子可以提取到行列式的外面
- 若行列式某行(或列)元素全为零,则该行列式值为零
- 若行列式某两行(或列)元素相同或者成比例,则该行列式值为零
\[\left[
\begin{matrix}
a_1+b_1 & c_1 \\
a_2+b_2 & c_2 \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
a_1 & c_1 \\
a_2 & c_2 \\
\end{matrix}
\right]
+
\left[
\begin{matrix}
b_1 & c_1 \\
b_2 & c_2 \\
\end{matrix}
\right]
\]
\[\left[
\begin{matrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{i1} & a_{i2} & \cdots & a_{in} \\
\vdots & \vdots & \ddots & \vdots \\
a_{j1} & a_{j2} & \cdots & a_{jn} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{matrix}
\right]=
\left[
\begin{matrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{i1} & a_{i2} & \cdots & a_{in} \\
\vdots & \vdots & \ddots & \vdots \\
a_{j1}+ka_{i1} & a_{j2}+ka_{i2} & \cdots & a_{jn}+ka_{in} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{matrix}
\right]
\]
矩阵
矩阵是一个表格
定义
- 矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合, 有m行n列
- n阶方阵:当\(m==n\)时,称为n阶方阵
- 同型矩阵:两个矩阵行数和列数相等
- 相同矩阵:两个矩阵一摸一样
- 零矩阵:所有元素都为0
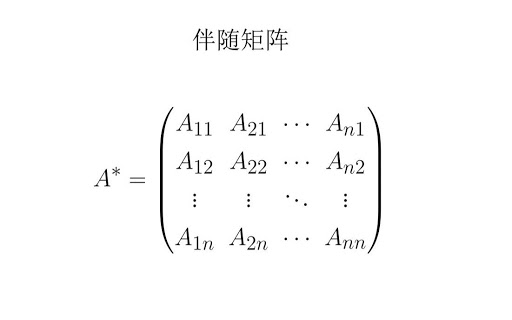
- 伴随矩阵:先为n阶方阵,变成一个只有数值相等的行列式,求出所有的余子式进行排列,得出的新的矩阵就为伴随矩阵,记作\(A^*\),\(A*A^*=A^**A=|A|E\)
- 矩阵合同:A,B为n阶实对称方阵,若存在可逆矩阵P,使得\(P^TAP=B\),称A,B合同。A,B合同的充分必要条件为A,B的特征值中正,负及零的个数相同
- 正交矩阵:\(AA^T=E\),则\(A^{-1}=A^T\)
- 矩阵等价:矩阵A通过初等变换变成矩阵B,\(B=QAP\),则A,B矩阵等价。等价的充要条件为\(r(A)=r(B)\)
运算
- 加减乘,没有除法,乘法没有交换律
- 加减法:必须同型,对应元素相加减
- 一个数与矩阵乘,所有元素都乘
- 两个矩阵相乘:\(A_{m*n}*B_{n*s}=C_{m*s}\),内标同可乘,外标确定型,左边取行,右边取列

注意点
- \(A,B\)为两个矩阵
- \(A\neq 0\),\(B\neq 0\),得不出\(A*B\neq 0\)
- \(A\neq 0\) ,得不出\(A^k\neq 0\)
- \(A*B\neq B*A\)
性质
- \(|A^T|=|A|\)
- \((AB)^T=B^TA^T\)
- \(|AA^T|=|A|^2\)
- \(|A^*|=|A|^{n-1}\)
\[\left[
\begin{matrix}
A & 0 \\
0 & B
\end{matrix}
\right]
=
\left[
\begin{matrix}
A & C \\
0 & B
\end{matrix}
\right]
=
\left[
\begin{matrix}
A & 0 \\
D & B
\end{matrix}
\right]
=|A|*|B|
\]
- \(|kA|=k^n|A|\)
拉普拉斯法则\(A_{nn},B_{nn}\),\(|AB|=|A|*|B|\)
背景
- \(AX=b\) 表示线性方程组,\(A\)为n阶方阵,若存在n阶矩阵\(B\),使得\(BA=E\),则\(BAX=Bb\)得\(X=Bb\)

逆矩阵
定义
- \(A\)为n阶方阵,若存在n阶矩阵\(B\),使得\(BA(AB)=E\),则称\(A\)可逆,\(B\)为\(A\)的逆阵,\(B\)=\(A^{-1}\)
求解方法
- 判断可逆的条件 \(A_{nn}\),\(A\)可逆充分必要\(|A|\neq 0\)
- 方法一 伴随矩阵法:\(A*A^*=|A|E\),则\(A* \dfrac{A^*}{|A|} =E\)
- 方法二 初等变换法
- \(E(i(k))\)代表第i行乘以k
- \(E(ij(k))\)代表的是第j行乘以k加到i行,或者第i列乘以k加到j列
- 利用\((A|E)\)进行操作
- 但如果找不出到n阶矩阵\(B\),则要研究矩阵的秩
秩
本质是方程组的约束条件的个数
定义
矩阵\(A_{m*n}\)中任取r行r阶而形成的r阶行列式,称为A的r阶子式。
- 如果\(\exists r\)阶子式不为零
- \(\forall r+1\) 阶子式都为零
则称A的秩为r,记r(A)=r
性质
- \(A_{n*n}\),\(|A|\not=0\)则\(A\)可逆,满秩\(r(A)=n\)
- \(A_{m*n}\),则\(r(A)<=min[n,m]\)
- \(r(A)=r(A^T)=r(AA^T)=r(A^TA)\) 。见到\(AA^T,A^TA\)用此性质
- \(A,B\)是同型矩阵,则\(r(A\pm B) \leq r(A) +r(B)\)。见到\(A+B,A-B,r(A)+r(B)\)用此性质
- \(\alpha ^T\beta\) 左转右不转为数,\(\alpha \beta ^T\) 左不转右转为矩阵
- \(A_{m*n},B_{n*s}\)则\(r(AB)\leq min [r(A),r(B)]\)。见到\(AB\)用此性质
- 若\(A=BP\),P可逆,则\(r(A)=r(B)\)
- \(A_{m*n},B_{n*s}\)且\(AB=0\)则\(r(A) +r(B)\leq n\)。见到\(AB=0\)用此性质
\[r(A^*)=
\begin{cases}
n,r(A)=n
\\
1,r(A)=n-1
\\
0,r(A)<n-1
\end{cases}
\]
- \(max(r(A),r(B))\leq r(\dfrac{A}{B})\leq r(A+B)\)
- \(max(r(A),r(B))\leq r(A|B)\leq r(A+B)\)
向量
定义
- 向量 :n维向量组,一般默认情况下是列向量
\[\alpha =
\begin{bmatrix}
a_1 \\ a_2 \\ a_3 \\ \cdots\\ a_n
\end{bmatrix}
\]
- 模是指向量的大小,\(|\alpha |=\sqrt{a_1^2+a_2^2+...+a_n^n}\) ,当\(\alpha ==1\) ,\(\alpha\)为单位向量或者规范向量
- \(\alpha^o= \dfrac{1}{|\alpha | }\alpha\) 是指\(\alpha\)的单位化
- 内积 \((\alpha ,\beta)=(\beta ,\alpha)=\alpha^T\beta=\beta^T \alpha=a_1*b_1+a_2*b_2+....a_n*b_n\)
- 正交:如果 \((\alpha ,\beta)==0\),称\(\alpha , \beta\)正交,记作\(\alpha \bot \beta\)
相关性
- 对于齐次线性方程组 \(x_1\alpha_1+x_2\alpha_2+....+x_n\alpha_n=0\)
- 若方程组只有零解,则称向量\(\alpha_1,\alpha_2,...\alpha_n\)线性无关,\(x_1=x_2=..=x_n=0\)
- 若方程组有非零解,则称向量\(\alpha_1,\alpha_2,...\alpha_n\)线性相关
线性表示
- 对于非齐线性方程组 \(x_1\alpha_1+x_2\alpha_2+....+x_n\alpha_n=b\)
- 若方程组有解,则称向量b可由向量\(\alpha_1,\alpha_2,...\alpha_n\)线性表示
- 若方程组无解,则称向量b不可由向量\(\alpha_1,\alpha_2,...\alpha_n\)线性表示
向量组的性质
- \(\alpha_1,\alpha_2,...\alpha_n\)线性相关充要条件\(\alpha_1,\alpha_2,...\alpha_n\)中至少有一个向量可由其余向量向量线性表示
- \(\alpha_1,\alpha_2,...\alpha_n\)线性无关,\(\alpha_1,\alpha_2,...\alpha_n,b\)线性相关,则b可由 \(\alpha_1,\alpha_2,...\alpha_n\)唯一线性表示
- 全组无关 \(\Rightarrow\) 部分组无关
- 部分组相关 \(\Rightarrow\) 全组相关
- \(\alpha_1,\alpha_2,...\alpha_n\)n个n维向量,则\(\alpha_1,\alpha_2,...\alpha_n\)线性相关的的充分必要条件为\(|\alpha_1,\alpha_2,...\alpha_n|=0\)
- \(\alpha_1,\alpha_2,...\alpha_n\)为n个m维向量,若\(m<n\),则\(\alpha_1,\alpha_2,...\alpha_n\)一定是线性相关
- 添加向量的个数提高相关性,添加维数提高无关性
向量组等价
- \(\alpha_1,\alpha_2,...\alpha_n\),\(\beta_1,\beta_2,...\beta_n\)是两个维度相等的向量组,若\(\beta_1,\beta_2,...\beta_n\)可由向量组\(\alpha_1,\alpha_2,...\alpha_n\)线性表示,\(\alpha_1,\alpha_2,...\alpha_n\)可由向量组\(\beta_1,\beta_2,...\beta_n\)线性表示,则两个向量组等价
极大线性无关组和秩
- 通俗的说就是把线性相关的垃圾扔掉
- 对于\(\alpha_1,\alpha_2,...\alpha_n\),存在r个向量线性无关,任意r+1个向量线性相关,则r个线性无关的向量组称为极大线性无关组,称r为向量组的秩
- 极大组不一定唯一
- \(\alpha_1,\alpha_2,...\alpha_n\)线性无关充要条件\(\alpha_1,\alpha_2,...\alpha_n\)为极大线性无关组充要条件\(\alpha_1,\alpha_2,...\alpha_n\)的秩为n
- \(A_{m*n},B_{n*s}=(\beta_1,\beta_2,...\beta_n),AB=A(\beta_1,\beta_2,...\beta_n)=(A\beta_1,A\beta_2,...A\beta_n)\)
向量组秩的性质
- 矩阵A,则矩阵A的秩= A的行向量组的秩=A的列向量组的秩
- \(\alpha_1,\alpha_2,...\alpha_n\)线性相关, 则\(r(A)<n\)
- \(I_1=\alpha_1,\alpha_2,...\alpha_n\),\(I_2=\beta_1,\beta_2,...\beta_n\),如果\(I_1\)可由\(I_2\)线性表示,则\(r(I_1)<r(I_2)\)
- 等价的向量组秩相等
- 研究一组向量组的秩和矩阵的秩联系起来
等价转换
- \(AX=0\)

- \(AX=b\)

线性方程组
\[\begin{cases}
AX=0 \quad (*)
\\
AX=b \quad (**)
\end{cases}
\]
基本定理
- \((*)\)只有零解,则\(r(A)=n\)
- \((*)\)非零解,则\(r(A)<n\)
- \((**)\)无解,则\(r(A)\neq r(\overline{A})\)
- \((**)\)有解,则\(r(A)= r(\overline{A})\)
- \(X_1,...,X_N\)为\((**)\)的一组解,则\(k_1X_1,...,k_nX_N\)为\((**)\)的解充分必要条件为\(k_1+...+k_n=1\)
- \(X_1,...,X_N\)为\((**)\)的一组解,则\(k_1X_1,...,k_nX_N\)为\((*)\)的解充分必要条件为\(k_1+...+k_n=0\)
- \(A_{m*n},B_{n*s}=(\beta_1,\beta_2,...\beta_n),AB=0\),则\(\beta_1,\beta_2,...\beta_n\)为\(AX=0\)的解
- \(A_{m*n}\)该向量组所含的解向量的个数\(S=n-r(A)\)
求通解
- 先阶梯化,找到自由变量和约束变量
- 非齐的通解=齐次的通解+一个特解

矩阵的特征值和特征向量
定义
- \(A_{n*n}\)(研究对象的是方阵),存在\(\lambda\)(一个数),存在向量\(\alpha(\alpha \not= 0)\),使得 \(A\alpha=\lambda \alpha\),\(\lambda\)就叫特征值,\(\alpha\)叫做特征向量
- \(A\alpha=\lambda \alpha\),\((\lambda -A) \alpha=0\),则\(AX=0\)存在非零解,则\(|\lambda E-A|=0\)
- 特征方程 \(|\lambda E-A|=0\)
- 矩阵相似:\(A,B\)都为n阶矩阵,若存在可逆矩阵P,使得\(P^{-1}AP=B\),称A,B相似,记作\(A\)~\(B\)
概念认知
- 特征方程 \(|\lambda E-A|=0\)解得 \(\lambda_1,\lambda_2,...,\lambda_n\)
- \(\lambda_1+\lambda_2+,...,+\lambda_n=a_{11}+a_{22}+..+a_{nn}=tr(A)=(\alpha ,\beta)\)(\(tr(A)\)为A的迹)
- \(\lambda_1\lambda_2...\lambda_n=|A|\)
- 设\(\lambda_0\)为特征值,\(\lambda_0\)对应的特征向量为\((\lambda_0 E-A)X=0\)的非零解
- 若\(A\)~\(B\),则\(|\lambda E-A|=|\lambda E-B|\),A,B的特征值相等,反之不成立
- 若\(A\)~\(B\) ,则\(|A|=|B|,tr(A)=tr(B)\)
一般性质
重要性质对于\(A_{n*n}\)的特征值\(\lambda_1,\lambda_2(\lambda_1 \not=\lambda_2)\), \((\lambda_1 E-A)X=0\)解的基础解系为\(\alpha_1,...\alpha_n\), \((\lambda_2 E-A)X=0\)解的基础解系为\(\beta_1,...\beta_n\),
则\(\alpha_1,...\alpha_n,\beta_1,...\beta_n\)线性无关- 对于\(A\alpha=\lambda_0 \alpha\),\(f(A)\alpha=f(\lambda_0)\alpha\)
- 若\(A\)可逆,则\(A^{-1}\alpha=\dfrac{1}{\lambda_0}\alpha\),\(A^{*}\alpha=\dfrac{|A|}{\lambda_0}\alpha\),说明\(A^{*},A^{-1},A\)公用一个特征向量
- 对于\(A_{n*n}\),则A可相似对角化充要条件A有n个线性无关的特诊向量
- A为方阵,\(r(A)\geq\)非零特征值的个数
- A可对角化,则\(r(A)=\)非零特征值的个数
- A为n阶方阵,则\(n=\)特征值的个数,重数算多个
- \(A=\alpha \beta^T\),则\(tr(A)=(\alpha, \beta)\)(矩阵写出来就明白了)
实对称矩阵性质
以下所有的的性质都是只有实对称矩阵才拥有的性质
- \(A^T=A\)
- \(\lambda_1 \not=\lambda_2\),\(A\alpha=\lambda_1 \alpha\),\(A\beta=\lambda_2 \beta\),可得\(\alpha \bot \beta\)
- \(A^T=A \Longrightarrow \lambda_i\in R(1\leq i\leq n)\)
- \(A^T=A \Longrightarrow\) A可对角化
施密特正交化
- 正交化

- 规范化(通俗点讲就是单位化)
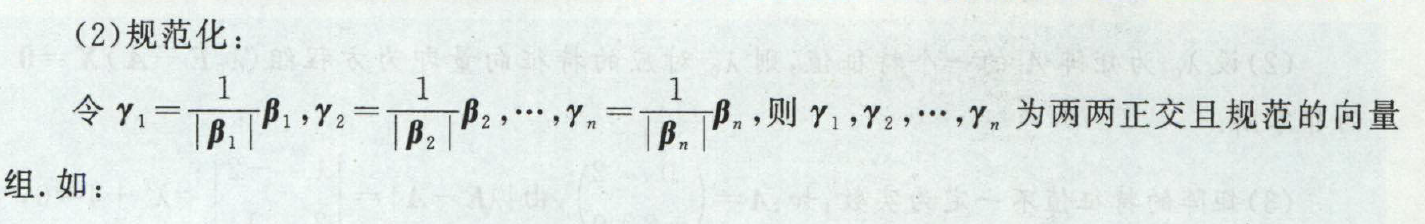
正交矩阵
定义
对于\(A_{n*n}\),若\(A^TA=E\),则称A为正交矩阵
性质
- \(A^T=A^{-1}\)
- \(|A^T|*|A|=1\),\(|A|^2=1\),\(|A|=\pm 1\)
充要条件
- \(Q=(\gamma_1,...,\gamma_n)\),\(Q^TQ=E\)充要条件为\(\gamma_1,...,\gamma_n\)两两正交且单位
对角化过程
\(A^T\not=A\)不是实对称矩阵的情况
- \((\lambda E-A)X=0\) ,求出特征值 \(\lambda_1,..,\lambda_n\)
- \((\lambda_i E-A)X=0\) ,求出所有的基础解系 \(\alpha_1,...\alpha_m(m\leq n)\) ,所有基础解系线性无关
- 若\((m\leq n)\),A不可对角化
- 若\((m== n)\),A可对角化 ,\((A\alpha_1,A\alpha_2,...A\alpha_n)=(\lambda_1\alpha_1,\lambda_2\alpha_2,...,\lambda_n\alpha_n)\),得
\(AP=P*\)对角化解
\(A^T=A\)是实对称矩阵的情况
- \((\lambda E-A)X=0\) ,求出特征值 \(\lambda_1,..,\lambda_n\)
- \((\lambda_i E-A)X=0\) ,求出所有的基础解系 \(\alpha_1,...\alpha_n\) 必定为n,个数不会少,必定可以对角化,所有基础解系线性无关
- 方法一:找可逆阵P
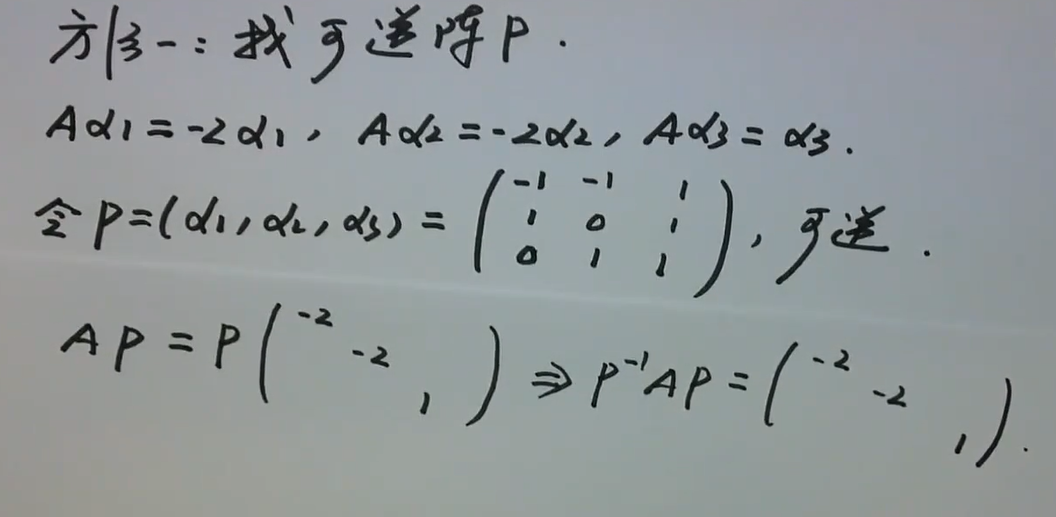
- 方法二:施密特正交化,求出\(Q=(\gamma_1,...,\gamma_n)\) ,得
\(AQ=Q*\)对角化解
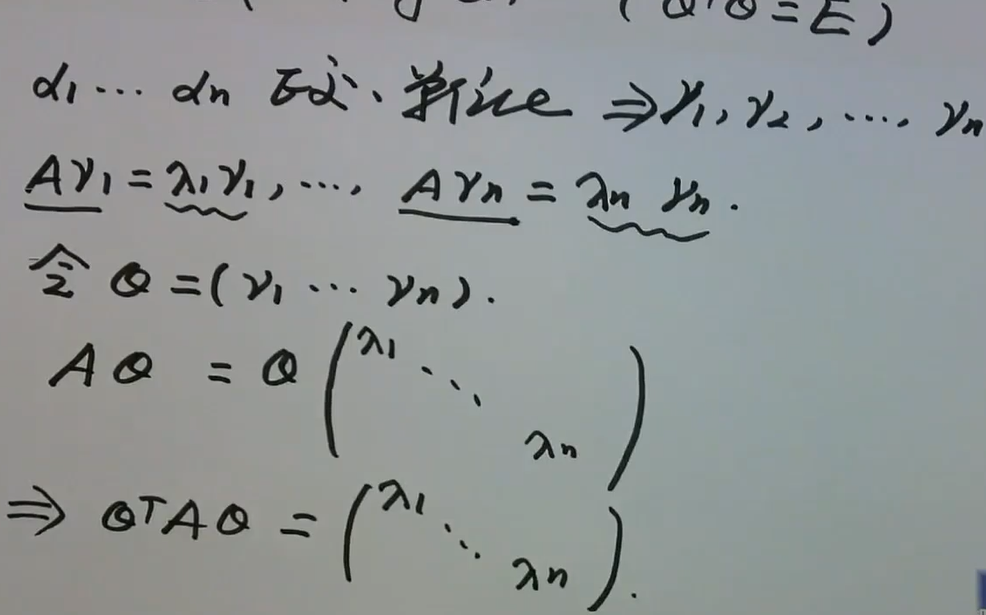
λ的求法
- 公式法:\(|\lambda E-A|=0\)
- 定义法:\(A\alpha =\lambda \alpha(\alpha \not=0)\)
- 关联法:
\[\begin{cases}
A^{-1},A^{*},A 特征向量相同
\\
P^{-1}AP=B,AB相似,AB特征值相等
\end{cases}
\]
矩阵对角化的判断
- 若\(A^T=A\),则A可对角化
- 若\(A^T\not =A\) ,先求出特征值 \(\lambda_1\lambda_2...\lambda_n\),若满足下列条件之一(1)\(\lambda_1\lambda_2...\lambda_n\)单值(2)每个特征值重数与无关特侦向量个数一致,则A可对角化
判断两个矩阵是否相似
- \(|\lambda E-A|=|\lambda E-B|\),即为 \(\lambda\)必须相等


求A^m

二次型
顾名思义就是二次多项式,例如\(f(x_1,x_2,x_3)=2x_1^2-3x_2^2+x_3^2\)就是一个二次型
定义
- 二次型:含n个变量\(x_1,..,x_n\),且每次都是二次的齐次多项式,则\(f(x)=X^TAX\)
- 标准二次型:只有平方项,充要条件为A为对角矩阵
- 非标准二次型:有交叉项,譬如\(f(x_1,x_2,x_3)=2x_1x_2\),充要条件为A为实对称矩阵但不对角
- 规范二次型:系数为1和-1的标准型,称为二次型的规范形
- 二次型的标准化
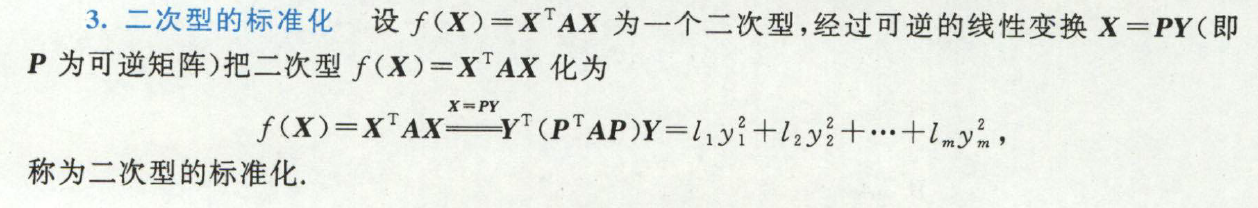
- 矩阵合同:A,B为n阶方阵,若存在可逆矩阵P,使得\(P^TAP=B\),称A,B合同。A,B合同的充分必要条件为A,B的特征值中正,负及零的个数相同
标准化
原来不标准变成标准
- 配方法

- 正交变换法

正定二次型
定义
- 对于二次型\(f(x_1,x_2,...,x_n)=X^TAX\),若对任意\(X \not =0\),总有\(X^TAX>0\),则称\(X^TAX\)为正定二次型,A称为正定矩阵。
- 例如:\(f(x_1,x_2,x_3)=2x_1^2+3x_2^2+x_3^2\),对于任何的\(x_1,x_2,x_3\)有\(f(x_1,x_2,x_3)\geq0\),若\(f(x_1,x_2,x_3)=0\)当且仅当\(x_1=x_2=x_3=0\),或对任意\(X\not = 0,X^TAX>0\)
判别方法
- 二次型\(X^TAX\)为正定二次型的充分必要条件为A的特征值全为正数



