考研高等数学基础知识
前言
博客园还支持数学公式1 数学公式2 数学符号 输入还是不错的(｀・ω・´)记录这些基本知识点是为了方便自己以后忘了可以看看。数学真是一门很灵活的学科。= v =
函数，极限，连续
求极限
直接带入
函数值和在这边的极限没有关系，但是利用函数连续性：lim f(x) = f(a) x->a可以通过直接带入x的值快速的求出极限值,前提是这个函数是连续的。
等价替代
值得注意的是，加减方面尽量不要替代，会使精度降低，将复杂的式子替换成下面的公式，使其能进行简化操作得出答案
- \(x\) ~ \(sinx\) ~ \(tanx\) ~ \(arcsinx\) ~ \(arctanx\) ~ \(ln(1+x)\) ~ \(e^x-1\)
- \((1+x)^d-1\) ~ \(dx\)
- \(1-cosx\) ~ \(\dfrac{1}{2} x^2\)
- \(a^x-1\) ~\(xlna\)
- \((1+x)^{\dfrac{1}{x}}\) ~ \(e\) (很好用)
- \(x-arctanx\) ~ \(\dfrac{x^3}{3}\)
- \(x-sinx\) ~ \(\dfrac{x^3}{6}\)
洛必达和夹逼准则
- 分子分母分别求导再求极限，洛必达之后的式子没极限不一定原式没极限。
- 找出一个比原式小的式子和一个比原式大的式子证明他们两的极限相同为a，则原式极限也为a
利用泰勒公式
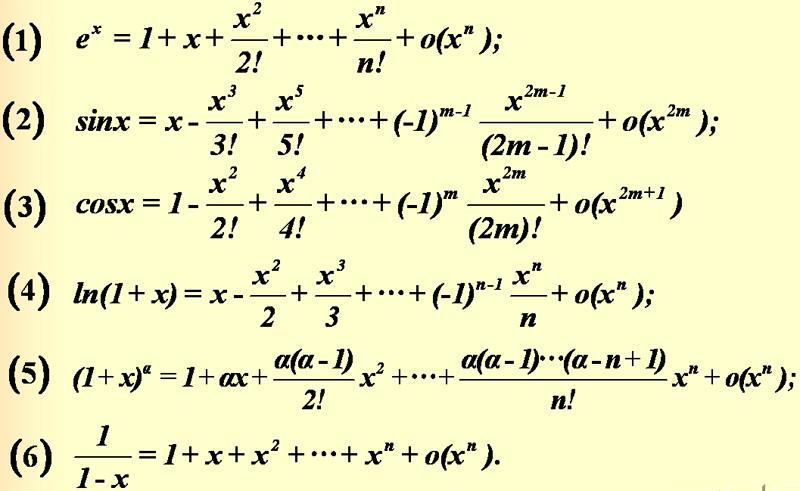
三角函数
等价变换
-
\(cotx=\dfrac{1}{tanx}\) ; \(secx=\dfrac{1}{cosx}\) ; \(cscx=\dfrac{1}{sinx}\); \(cos2x=cos^2x-sin^2x\)
-
\(sin2x=2sinxcosx\); \(sin(x+y)=sinxcosy+cosxsiny\)
-
\(1+cos2x=2cos^2x\); \(sinx-cosx=\sqrt{2}sin(x- \dfrac{\pi}{4})\)
-
\(cos(x+y)=cosxcosy-sinxsiny\);
求导
- \((arcsinx)'=\dfrac{1}{\sqrt{1-x^2}}\) ; \((arccosx)'=-\dfrac{1}{\sqrt{1-x^2}}\) ; \((arctanx)'=\dfrac{1}{1+x^2}\) ; \((arccotx)'=-\dfrac{1}{1+x^2}\)
间断点
导数与微分
导数定义
- \(f'(x_0)=\lim\limits_{x\rightarrow x_0}\dfrac{f(x)-f(x_0)}{x-x_0}\);
- 或\(f'(x_0)=\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\);
- 或\(f'(x_0)=\lim\limits_{h \rightarrow 0}\dfrac{f(x_0+h)-f(x_0)}{h}\);
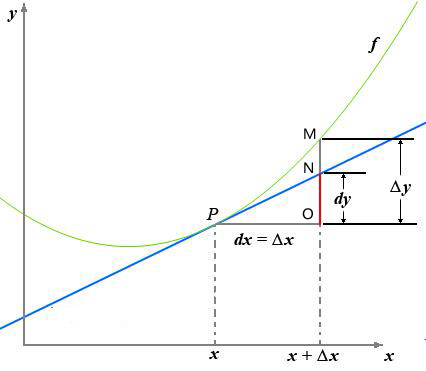
dy和△y的关系
- \(Δx\)是有限小的量，\(dx\)是无限小的量
- dy：表示微分 \(dy = f'(x)dx\)
- Δy：表示函数的增量 \(△y = f(x+dx) - f(x) = f'(x)dx + o(dx)\)
- \(△y-dy= o(dx)\)
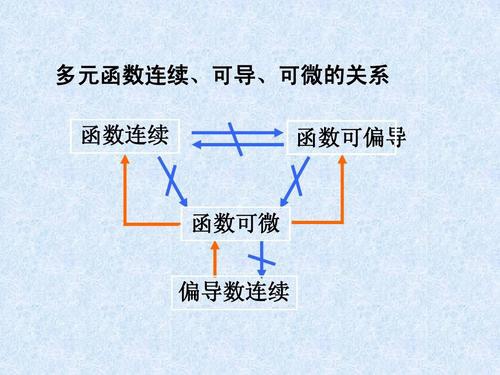
连续，可导，可微
- 可导一定连续，连续不一定可导，可导和可微条件一样
- 以在\(x_0\)处讨论问题
- 连续条件 \(f(x_0^-)=f(x_0^+)=f(x_0)\)
- 可导和可微条件 先连续 \(f'(x_0^-)=f'(x_0^+)\)
中值定理和一元函数微分学的应用
中值定理
罗尔中值定理
- 在闭区间 [a,b] 上连续
- 在开区间 (a,b) 内可导
- f(a)=f(b)，则至少存在一个 ξ∈(a,b)，使得 f'(ξ)=0。
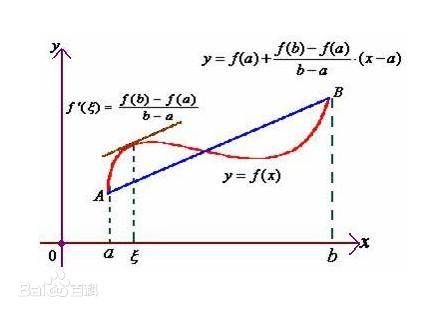
拉格朗日中值定理
- 在闭区间[a,b]上连续；
- 在开区间(a,b)内可导
- 那么在开区间(a,b)内至少有一点\(ξ(a<ξ<b)\) 使等式 \(f(b)-f(a)=f'(ξ)(b-a)\)成立。
柯西中值定理
- 柯西（Cauchy）中值定理：设函数f(x),g(x) 满足
- 在闭区间[a,b] 上连续；
- 在开区间(a,b) 内可导；
- 对任意(a,b)那么在 内至少有一点 \(ξ(a<ξ<b)\)，使得 成立\(\dfrac{f(b)-f(a)}{g(b)-g(a)}=\dfrac{f'(ξ)}{g'(ξ)}\)
弧微分
- 弧微分是用一条线段的长度来近似代表一段弧的长度，利用MT的长度近似的代表MM'的长度。
- \((ds)^2=(dx)^2+(dy)^2=(dx)^2+(y'dx)^2\)
- \((ds)=\sqrt{1+(y')^2}dx\)
- 参数方程 \(x=f(t),y=f(t)\)时\(ds=\sqrt{(\dfrac{df(t)}{dt})^2+(\dfrac{dg(t)}{dt})^2}dt\)
曲率
- 曲线的曲率（curvature）就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。
- 曲率 \(K=\dfrac{|y''|}{(1+y'^2)^\dfrac{3}{2}}\)
- 曲率半径 \(\rho=\dfrac{1}{K}\)
不定积分
概念
\(F(x)'=f(x)\) 即 \(\int f(x)=F(x)+C\)( C不要忘记 )
常用不定积分
- \(\int \dfrac{1}{1+cosx}dx= tan\dfrac{x}{2}+C\)
- \(\int secxdx= ln|secx+tanx|+C\)
- \(\int sec^2xdx= tanx+C\)
- \(\int cscxdx= ln|cscx+tanx|+C\)
- \(\int csc^2xdx= -cotx+C\)
- \(\int\dfrac{1}{\sqrt{x^2+a^2}}dx= ln(x+\sqrt{x^2+a^2})+C (x=atant)\)
- \(\int\dfrac{1}{\sqrt{x^2-a^2}}dx= ln(x+\sqrt{x^2-a^2})+C (x=asect)\)
- \(\int \sqrt{a^2-x^2} dx=\dfrac{a^2}{2}arcsin\dfrac{x}{a}+\dfrac{1}{2}x \sqrt{x^2-a^2} +C (x=asint)\)
分部积分法
\(\int u dv=uv-\int vdu\)
以下5种情况直接使用分部积分法
- \(\int x^ne^x dx =\int x^n de^x\)
- \(\int x^nlnx dx =\int lnx d\dfrac{1}{n+1}x^(n+1)\)
- \(\int x^n*\) 三角函数 \(dx\) (三角靠后) \(sinx,cosx\)为1次否则降次,\(tanx,secx,cotx,cscx\)为偶数次
- \(\int x^n*\) 反三角函数 \(dx\) (\(x^n\)靠后)
- \(I=\int e^asinx(cosx) dx\) (都能靠后)
- \(\int sec^nx(csc^nx) dx\) (其中n为奇数)
定积分
概念
\(\lim\limits_{\lambda\rightarrow0} \sum_{i=1}^nf(\xi_i) \Delta x_i = \int^a_bf(x)dx\)
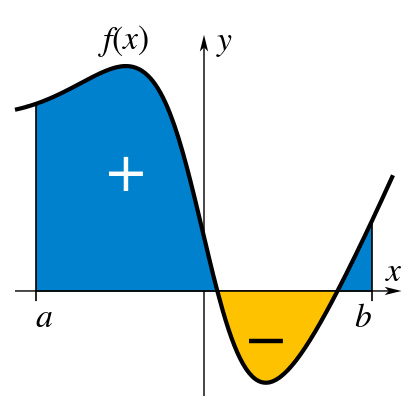
是一个函数与x轴形成的面积(可正可负)
性质
- \(\int^a_b[f(x)\pm g(x)] dx=\int^a_b f(x)dx\pm \int^a_b g(x)dx\)
- \(\int^a_b kf(x)dx =k\int^a_b f(x)dx\)
- \(\int^a_b f(x)dx =\int^a_c f(x)dx+\int^c_b f(x)dx\)
- 积分中值定理 \(f(x)\epsilon[a,b]\),存在\(\xi\epsilon[a,b]\)使得\(\int^a_b f(x)dx=f(\xi)(b-a)\)
- \([\int^x_af(x)dx]'=f(x)\)
- \([\int^{\varphi (x)} _af(x)dx]'=\varphi'(x)f(\varphi(x))\)
- \(\int^a_{-a} f(x)dx =\int^a_0[f(-x)+f(x)]dx\) 根据函数奇偶性操作
- \(\int^\pi_0 xf(sinx)dx = \dfrac{\pi}{2} \int^\pi_0 f(sinx)dx\)
- 若\(f(x)\)以\(T\)为周期的连续函数，对于任何a,总有
\(\int^{a+T}_a f(x)dx =\int^T_0 f(x)dx\)
\(\int^{nT}_0 f(sinx)dx =n\int^T_0 f(x)dx\)
\[\int^\dfrac{\pi}{2}_0 sin^ndx=\int^\dfrac{\pi}{2}_0 cos^ndx
\begin{cases}
\dfrac{n-1}{n}\dfrac{n-3}{n-2}\dfrac{1}{2}\dfrac{\pi}{2}& \text{n为正偶数}\\
\dfrac{n-1}{n}\dfrac{n-3}{n-2}\dfrac{2}{3}& \text{n为大于1的奇数}
\end{cases}
\]
换元积分法
- \(\int^b _af(x)dx =\int^\beta _\alpha f[\varphi(t)] \varphi'(t)dt\)
分布积分法
- \(\int^a_b u dv=uv|^a_b -\int^a_b vdu\)
反常(广义)积分
- 积分区间无限,有第一类间断点 \(\lim\limits_{b\rightarrow\infty}[F(b)-F(a)]=A\) 或者发散
- 无界函数 \(\lim\limits_{\varepsilon\rightarrow0}[F(b)-F(a+\varepsilon)]=A\) 或者发散
Γ函数
- 定义： \(\Gamma(\alpha)=\int^\infty_0 e^{-x}x^{\alpha-1}dx (s>0)\)
- \(\Gamma(\alpha+1)=\alpha \Gamma(\alpha)\)
- \(\Gamma(n+1)=n!\)
- \(\Gamma(\dfrac{1}{2})=\sqrt{\pi}\)
应用
元素法
若所求量\(U\)与\(x\)有关\(x\) \(\in[a,b]\)
- 取\([x,x+dx]\subset[a,b]\)
- \(dU=f(x)dx\)
- \(U=\int^b _af(x)dx\)
平面面积
- \(f(x)\) 和\(g(x)\)形成的面积 设(\(f(x)>=g(x)\))
其面积
\(S= \int^b _a[f(x)-g(x)]dx\) - 平面域D由曲线\(\rho=\rho(\theta),\theta=\alpha,\theta=\beta(\alpha<\beta)\)其面积\(S=\dfrac{1}{2}\int^\alpha_\beta\rho^2(\theta)d\theta\)
旋转体体积
- 绕x轴形成体积 \(V_x=\pi\int^b _af^2(x)dx\)
- 绕y轴形成体积 \(V_y=2\pi\int^b _axf(x)dx\)
曲线弧长
- \(y=f(x),a\leq x \leq b 则S=\int^b _a\sqrt{1+y'^2}dx\)
- \(x=x(t),y=y(t)a\leq t \leq b则S=\int^b _a\sqrt{x'^2+y'^2}dt\)
- \(\rho=\rho(\theta),a\leq \rho \leq b 则S=\int^b _a\sqrt{\rho^2+\rho'^2}dx\)
旋转体侧面积
- 曲面\(y=f(x)(f(x)>=0)\) 和直线 \(x=a,x=b(0 \leq a <b)\)及x轴所围成区域绕x轴旋转体所得旋转体的侧面积为\(S=2\pi\int^b _axf(x)\sqrt{1+f'^2(x)}dx\)
微分方程
定义
含有导数和微分的方程
目标
我们的目标是得出\(y\)和\(x\)的关系式，比如一个函数很难求出y和x之间的关系，是一个隐函数，我们可以先求出\(\dfrac{dy}{dx}\),再通过微分方程求解就能得到y和x之间的关系，十分巧妙。
一阶微分方程
一阶可分离变换的微分方程
- \(\dfrac{dy}{dx}=\phi_1(x)\phi_1(y)\) (注意考虑y=0的情况)
- \(\int\dfrac{dy}{\phi_2(y)}=\int\phi_1(x)dx+C\)
- 例如\(\dfrac{dy}{dx}=x^2y\)
齐次微分方程
- \(\dfrac{dy}{dx}=\phi(\dfrac{y}{x})\)
- 令\(u=\dfrac{y}{x}\) \(y=ux\)
- \(\dfrac{dy}{dx}=u+x\dfrac{du}{dx}\)
一阶齐次线性微分方程
这个做法可以把上面两种做法简化
- \(\dfrac{dy}{dx}+P(x)y=0\) （注意考虑y=0的情况)
- \(y=Ce^{-\int P(x)dx }\)
一阶非齐线性微分方程
-
\(\dfrac{dy}{dx}+P(x)y=Q(x)\)
-
\(y=[\int Q(x)e^{\int P(x)dx}dx+C ]e^{-\int P(x)dx }\)
可降阶的高阶微分方程
目标：让阶数降低
- \(y^{(n)}=f(x)(n\geq2)\) 一次一次还原
- \(f(x,y',y'')=0(缺y)\) 令\(y'=p,y''=\dfrac{dp}{dx}\)带入即可
- \(f(y,y',y'')=0(缺x)\) 令\(y'=p,y''=\dfrac{dp}{dx}=p\dfrac{dp}{dy}\)带入即可
高阶线性微分方程
二阶常系数齐次线性微分方程
\(y''+py'+qy=0\)
特征函数为\(\lambda^2+p\lambda+q=0\)
先求特征方程，然后判断\(\Delta\)的判断通解方程式
- \(y=C_1e^{\lambda_1 x}+C_2e^{\lambda_2 x}\) (\(\Delta>0\))
- \(y=(C_1+xC_2)e^{\lambda_1 x}\) (\(\Delta=0\))
- \(y=e^{\alpha x}(C_1cos\beta x+C_2sin\beta x)\)(\(\Delta<0\), \(\lambda_{12}=\alpha\pm\beta i\))
同样的道理可以推广到高阶
二阶常系数非齐线性微分方程
\(y''+py'+qy=f(x)\)
求解步骤
- \(y''+py'+qy=0\)通解
- \(y''+py'+qy=f(x)\)的一个特解\(y_0(x)\)
- \(f(x)=e^{kx} P_m(x)\)
按照\(P_m(x)\)的样式设\(y_0=P_m(x)e^{kx}\)如果发现解\(\lambda==k\) 则\(y_0=x*P_m(x)e^{kx}\)
- \(f(x)=e^{αx}[P(x)cosβx+Q(x)sinβx]\)
- 看右边，如果有指数函数提出去
- 按照右边的样子假设，设为\((asinkx+bcoskx)\)
- 如果\(\alpha+\beta i==\lambda\) ,则前面乘\(x\)
多元函数微分学
定义
\(D\)为区域,\(x,y,z\)为变量,如果 \(\forall (x,y) \in D\)， \(\exists \mid z与(x,y)\)对应，称为\(z\)为\(x,y\)的函数，记\(z=f(x,y)\)
极限
\(\lim\limits_{x\rightarrow x_0 y\rightarrow y_0}f(x,y)=A\)
求解方式和一元函数微分学差不多
性质
- 考虑这些性质的前提都是在区域\((x,y) \in D\)上函数是连续的
- 最值定理，最大值为M，最小值为m
- 有界定理 \(\exists k>0\) ，\(\forall (x,y) \in D\) ，\(|f(x,y)|\leq k\)
- 介值定理
偏导数
- 对x求导就叫x的偏导数，对y求导就叫y的偏导数,对x和y求导就叫偏导数
- 二阶偏导数 \(f''xy=f''yx\)
- 显函数求偏导，直接求
- 复合函数求偏导，能带入就带入，不能带入分别对\(u,v\)求偏导
- 隐函数求偏导
- 变换求偏导
全微分
- 如果 \(Δz=AΔx+BΔy+o(p)\) \(p=\sqrt{x^2+y^2}\)，称\(f(x,y)\)在\((x_0,y_0)\)处可全微分
- \(dz \mid_{(x_0,y_0)}=Adx+Bdy\)
连续性，可偏导性和可微性
例如我们在\((0,0)\)处讨论此问题
连续性
- 看能不能把\(x,y\)看成一个整体,转变成一元函数求极限
- 夹逼定理
可偏导性
- 判断\(\lim\limits_{x\rightarrow0} \dfrac{f(x,0)-f(0,0)}{x}\)和\(\lim\limits_{y\rightarrow0} \dfrac{f(0,y)-f(0,0)}{y}\)是否存在，如果都存在就可偏导
可微性
- 全增量减去（对x的偏导数乘以x的增量）减去（对y的偏导数乘以Y的增量）之差的距离是高阶无穷小
- \(Δz-f'_x(0,0)x-f'_y(0,0)y\)是p的高阶无穷小，\(p=\sqrt{x^2+y^2}\)即为可微
求极值
无条件极值
- 求出定义域 \(D\)
- 由\(\dfrac{\partial z}{\partial x}=0\) 和\(\dfrac{\partial z}{\partial y}=0\) 求出\(z=f(x,y)\)的驻点\((x_0,y_0)\)
- \(A=f''xx(x_0,y_0)\)，\(B=f''xy(x_0,y_0)\)，\(C=f''yy(x_0,y_0)\)
- \(AC>B^2\) ，\((x_0,y_0)\)为\(z=f(x,y)\)的极值点，\(A>0\)为极小值点，\(A<0\)为极大值点
- \(AC<B^2\)，\((x_0,y_0)\)不是函数的极值点
条件极值
\(\varphi(x,y)=0\)为约束条件，\(z=f(x,y)\)
拉格朗日乘数法
- \(F=f(x,y)+\lambda\varphi(x,y)\)
\[\begin{cases}
F_x'=f_x'+\lambda\varphi'_x=0
\\
F_y'=f_y'+\lambda\varphi'_y=0
\\
F_\lambda'=\varphi(x,y)=0
\end{cases}
\]
- 求出\(\lambda\)和\(x,y\)的值并确定最优解
重积分
定义
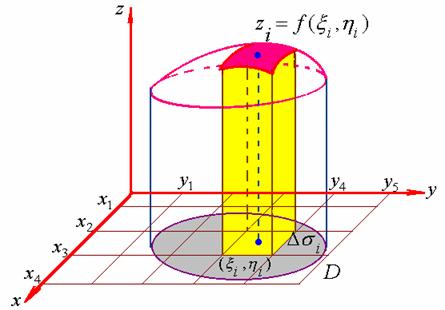
\(\lim\limits_{\lambda\rightarrow0} \sum_{i=1}^nf(\xi_i,\eta_i) \Delta a_i = ∬ \limits_{D} f(x,y)da\)
是一种可正可负的体积
性质
- \(∬ \limits_{D} [af(x,y)+bg(x,y)]da=a∬ \limits_{D} f(x,y)da+b∬ \limits_{D} g(x,y)da\)
- \(D=D_1+D_2,D_1\bigcap D_2=0\)，则\(∬ \limits_{D} f(x,y)da=∬ \limits_{D_1} f(x,y)da+∬ \limits_{D_2} f(x,y)da\)
- \(∬ \limits_{D} 1da=A\)，\(A\)为区域面积
- 积分中值定理 \(∬ \limits_{D} f(x,y)da=Af(\xi,\eta)\)
求解方法
直角坐标计算
- 先\(y\)后\(x\) : \(∬ \limits_{D} f(x,y)d\sigma=\int ^b_adx\int ^{φ_2(x)}_{φ_1(x)}f(x,y)dy\)
- 先\(x\)后\(yx\) : \(∬ \limits_{D} f(x,y)d\sigma=\int ^d_cdy\int ^{φ_2(y)}_{φ_1(y)}f(x,y)dy\)
极坐标计算
- 特征被积函数 \(f(x,y)\)中含有\(x^2+y^2\)，积分区域\(D\)的边界曲线含\(x^2+y^2\)
- \(x=rcos\theta\)，\(y=rsin\theta\)
- 先\(\theta\)后\(r\) :\(∬ \limits_{D} f(x,y)d\sigma=\int ^\beta_\alpha d\theta\int ^{r_2(\theta)}_{r_1(\theta)}rf(rcos\theta,rsin\theta)dy\)
