ACM基础板子
新生赛以后就正式成为一名acmer啦 ~虽然没有打过比赛
要好好学算法，拿一个牌嘛~
这里就记录算法学习情况，也怕自己偷懒，学一个就记录，看看长时间拖更就是在摸鱼，摸鱼和鸽子都是本质 ，加油！
开坑时间 2020.12.9
2020.12.9 今日快排走起（加模板）
quicksort!
void quicksort(ll a[],ll l,ll r)
{
if(l>r) return ; //递归跳出条件
ll temp=a[l]; ll i=l; ll j=r; //基准态定义和l,r定义
while(i!=j) //i,j不碰头
{
while(a[j]>=temp&&i<j) j--; //注意i<j条件，不然存在相等的数就无法跳出循环
while(a[i]<=temp&&i<j) i++; //同上
if(i<j) swap(a[i],a[j]);
}
a[l]=a[i]; //基准态交换
a[i]=temp;
quicksort(a,l,i-1); //递归
quicksort(a,i+1,r);
}
快排是分治的思想，设定一个基准态，将比基准态小的数放在左边，将比基准态大的数放在后边，然后将基准态归位，完成一个调整,这样一来部分数顺序已经调整，在分成左右区间进去递归，重复上述过程，已经归位的基准态不用管，（l,i-1）和(i+1,r)进行下一步递归，此时i为已经归位的数不需要再次递归。
个人理解： 快排原理是根据已经排好的数有一个规律：比n小的在n左边，比n大的在n的右边，所以左右遍历调整错误顺序数的位置，最后遍历完后（i==j)时，左右均已经遍历完，此时基准态归位完成一个循环，再进行区间二分，进行递归。
时间复杂度: 平均O(n)=nlogn,最坏的情况会退化到O(n)=n^2，最好情况也是O(n)=nlogn.
sort大法好
2020.12.10 分治里面归并少不了
mergesort!
int temp[200000]; //归并需要额外的空间存放调整完后的数据
void merge_sort(int q[], int l, int r)
{
if(l>=r) return;
int mid=l+r >> 1;
merge_sort(q,l,mid) , merge_sort(q,mid+1,r); //分解
// 调整顺序
int k=0, i=l, j=mid+1;
while(i<=mid&&j<=r)
if(q[i]<=q[j]) temp[k++]=q[i++];
else temp[k++]=q[j++];
while(i<=mid) temp[k++]=q[i++];
while(j<=r) temp[k++]=q[j++];
for(i=l,j=0;i<=r;i++,j++) q[i]=temp[j];
}
y总的一个函数完成归并模板orz 记录一下
归并排序：思路也是分治思想，先分成若干小部分，在单独递归处理后，合并在一起。为了满足数组有序，我们可以一直二分到子数组只有两个数，在一个个调整顺序，最后左右两边实行最后一次合并到另外一个数组中,完成所有排序。如下图：
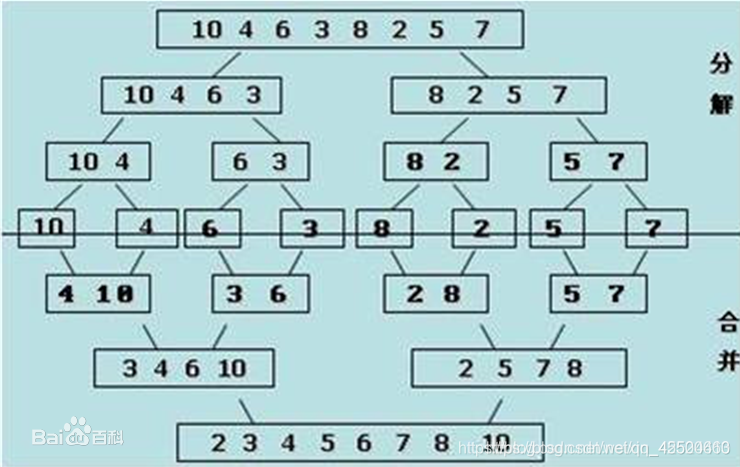
调整顺序中： 用两个指针指向两个子数组的头，相互比较，把较小的数存在temp数组中，然后把指向原数的指针向后移动一位，继续比较重复上述过程，如果某个指针到头了，就把另外剩下的数全部补在temp数组中完成一次调整顺序，最后把temp数组中的数据移动在需要排序的数组中即可。
确实很强呐
2020.12.12 二分查找板子来一个~
half_find!
自己的中式英语
binary_find
别问11号干嘛去了，问就是摸鱼去了 （比赛加摸鱼）
int half_find(int a[],int l,int r,int b)
{
while(l<r)
{
int mid=l+r >>1;
if(a[mid]>b) r=mid; //这里判断条件改动与lower_bound和upper_bound用法一致
else l=mid+1;
}
return l;
}
二分的板子边界一堆，直接记忆这个 实在不行stl大法好嘛 ，尽量自己写，简单的板子好记，原理也简单，记住if后不加，else后加1就行~，主要是边界问题难受最后return l和r一样的，因为此时l==r。
y总yyds
2020.12.14 静态链表(单链表)（数据结构冲冲冲）
Linked_list(Static)！
别问...13号干嘛去 gugugu 湖南停电停水大学实锤
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cstdio>
#include<cmath>
#define int ll
#define ll long long
using namespace std;
ll val[200000];
ll p[200000];
ll idx;
ll head;
void init() //创建静态单链表
{
head=-1;
idx=0;
}
void head_add(ll x) //在head处插入结点
{
val[idx]=x,p[idx]=head;
head=idx++;
}
void nor_add(ll k,ll x) //在k处插入一个结点
{
val[idx]=x,p[idx]=p[k];
p[k]=idx++;
}
void nor_remove(ll k) //把k后的一个结点删除
{
p[k]=p[p[k]]; //p[k++]不对注意！
}
void head_remove()
{
head=p[head];
}
ll n;
ll x,y;
char a;
signed main()
{
cin>>n;
init();
while(n--)
{
cin>>a;
if(a=='H')
{
cin>>x;
head_add(x);
}
else if(a=='D')
{
cin>>x;
if(x) nor_remove(x-1);
else head_remove();
}
else if(a=='I')
{
cin>>x>>y;
nor_add(x-1,y);
}
}
for(int i=head;i!=-1;i=p[i])
{
cout<<val[i]<<" ";
}
cout<<endl;
return 0;
}
总结一下所谓静态链表：用数组模拟链表（原因： 动态链表非常非常耗时间，malloc和new速度很慢，对acmer很不友好），用双数组模拟链表，实现某些功能（树图警告⚠），val表示实际存入的值，p表示下一个数的下标（等价于链表），再加上一个head表示头指针，idx表示剩余空间的第一位下标，可调用，创建新结点）(又是一个用空间换时间的）
几种基本操作：
1.创建新链表
void init() //创建静态单链表
{
head=-1;
idx=0;
}
将head指向-1（表示null)，idx=0表示数组均可用。
2.添加结点
void head_add(ll x) //在head处插入结点
{
val[idx]=x,p[idx]=head;
head=idx++;
}
void nor_add(ll k,ll x) //在k处插入一个结点
{
val[idx]=x,p[idx]=p[k];
p[k]=idx++;
}
插入要分头插和其他结点插
头插需要修改head,其他就不要需分开
先创建一个结点，再将创建的结点指向k或者头指向的那一位，最后将头或者k指向创建的数组， 记住idx要++ 这一步与上一步可以合并（因为可用的已经用了一位idx要往后移一位）
3.删除结点
void nor_remove(ll k) //把k后的一个结点删除
{
p[k]=p[p[k]]; //p[k++]不对注意！
}
void head_remove()
{
head=p[head];
}
同理删除也要分头和其他y总翻车现场 还是head的问题，这里注意，代码里面有注意的，不能写成p[k++]因为有时候k++不一定是k后面那一位，要用p[p[k]]表示k后面那一位，与指针类似。
4.链表遍历
for(int i=head;i!=-1;i=p[i]) cout<<val[i]<<" ";
从head开始顺着p开始遍历，如果i==-1（即此时遇到尾结点，跳出循环），同样注意，后面不是i++，而是把p[k]给i，表示指针后移一位。
就这样自己晚个安 绝对不熬夜
2020.12.15 双链表！
#include<bits/stdc++.h>
#define int ll
#define ll long long
using namespace std;
const int N = 2e6;
ll val[N], l[N], r[N],idx;
ll m;
void init()
{
r[0]=1,l[1]=0;
idx=2;
}
void add(int k,int x) //k后
{
val[idx]=x,r[idx]=r[k],l[idx]=k;
l[r[k]]=idx,r[k]=idx++;
}
void remove(int k) //删除第k个点
{
r[l[k]]=r[k];
l[r[k]]=l[k];
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
init();
cin>>m;
while(m--)
{
string a;
int k,x;
cin>>a;
if(a=="L")
{
cin>>x;
add(0,x);
}
else if(a=="R")
{
cin>>x;
add(l[1],x);
}
else if(a=="D")
{
cin>>k;
remove(k+1);
}
else if(a=="IL")
{
cin>>k>>x;
add(l[k+1],x);
}
else if(a=="IR")
{
cin>>k>>x;
add(k+1,x);
}
}
for(int i=r[0];i!=1;i=r[i]) cout<<val[i]<<" ";
cout<<endl;
return 0;
}
双链表： 一个结点同时有指向左右两边的指针,L[]和R[]，没有头指针，将0，1分别做为链表的头尾。不含其他实际数值，在0,1之间插入删除，其他与单链表类似。注意双向都要考虑.
最后注意： 链表中不要出现++操作。要用指针，也就是数组对下一位进行操作，用R[]表示下一位，L[]表示上一位。
over~
2021.1.3新年快乐...~ gugugu
我，大鸽子，来更新了~ （逃
来一个快速幂板子和费马小定理
快速幂板子
ll qpow(ll a, ll x)
{
ll re = 1;
while(x)
{
if(x&1) re = re * a % M;
a = a * a % M;
x = x >> 1;
}
return re;
}
M为防止数太大除的余数，a为底数，x为指数，思想跟二分差不多，将质数一次循环就除二，底数自己乘一次减少计算机次数。
费马小定理
原公式： a ^ (p-1) = 1 (mod)
费马小定理主要是防止指数太大时，如果是求同余的数，可以大大减少指数的大小
升级公式 ： ( a ^ n ) % p = ( a ^ ( n % （p -1) ) % p )
也就是当n很大的时候，若p是质数， a 与p互质 ， n可以先与（p-1）取模以后再进行整体%P，因为两数同余，结果一样。
2021.1.10别问，问就是期末考试 咕咕咕
高精度板子整理
高精度加法
#include<bits/stdc++.h>
#define fp for(int i=1;i<=n;i++)
#define ll long long
using namespace std;
vector<ll> add(vector<ll> &A , vector<ll> &B)
{
ll lena=A.size();
ll lenb=B.size();
vector<ll> C;
ll t=0;
for(int i=0;i<lena||i<lenb;i++)
{
if(i<lena) t+=A[i];
if(i<lenb) t+=B[i];
C.push_back(t%10);
t/=10;
}
if(t) C.push_back(1);
return C;
}
int main()
{
string a,b;
vector<ll> A,B,C;
cin>>a>>b;
ll lena=a.size();
ll lenb=b.size();
for(int i=lena-1;i>=0;i--) A.push_back(a[i]-'0');
for(int i=lenb-1;i>=0;i--) B.push_back(b[i]-'0');
C=add(A,B);
ll lenc=C.size();
for(int i=lenc-1;i>=0;i--) cout<<C[i];
cout<<endl;
return 0;
}
用vector代替数组，因为有个size函数，方便操作，函数里面t有多重身份注意。
高精度减法
#include<bits/stdc++.h>
#define ll long long
#define s size()
#define pb push_back
#define vl vector<ll>
using namespace std;
bool cmp(vl &a,vl &b)
{
if(a.s!=b.s) return a.s>b.s;
for(int i=a.s-1;i>=0;i--)
if(a[i]!=b[i]) return a[i]>b[i];
return true;
}
vl sub(vl &a,vl &b)
{
ll lena=a.s;
vl c;
for(int i=0,t=0;i<lena;i++)
{
t=a[i]-t;
if(i<b.s) t-=b[i];
c.pb((t+10)%10);
if(t<0) t=1;
else t=0;
}
while(c.s>1&&c.back()==0) c.pop_back();
return c;
}
int main()
{
string A,B;
vl a,b,c;
cin>>A>>B;
ll lena=A.s;
ll lenb=B.s;
for(int i=lena-1;i>=0;i--) a.pb(A[i]-'0');
for(int i=lenb-1;i>=0;i--) b.pb(B[i]-'0');
if(cmp(a,b))
{
c=sub(a,b);
ll lenc=c.s;
for(int i=lenc-1;i>=0;i--) cout<<c[i];
cout<<endl;
}
else
{
c=sub(b,a);
ll lenc=c.s;
cout<<"-";
for(int i=lenc-1;i>=0;i--) cout<<c[i];
cout<<endl;
}
return 0;
}
减法的话要先判断减数和被减数的大小，先决定输出+，-号，（该代码未考虑负数的相减），然后通过cmp控制大的为被减数，再最后注意借位问题就好啦。
还要注意去掉前导0.
高精度乘法
先是高精度×小数
#include<bits/stdc++.h>
#define s size()
#define pb push_back
#define vl vector<long long>
typedef long long ll;
using namespace std;
vl mul(vl &a,ll b)
{
vl c;
ll lena=a.s;
for(int i=0,t=0;i<lena||t;i++)
{
if(i<lena) t+=a[i]*b;
c.pb(t%10);
t/=10;
}
while(c.s>1&&c.back()==0) c.pop_back();
return c;
}
int main()
{
string A;
ll b;
vl a,c;
cin>>A>>b;
ll lena=A.s;
for(int i=lena-1;i>=0;i--) a.pb(A[i]-'0');
c=mul(a,b);
ll lenc=c.s;
for(int i=lenc-1;i>=0;i--) cout<<c[i];
cout<<endl;
return 0;
}
把小数看成整体进行计算，同样注意要去掉前导0.
高精度*高精度
#include<bits/stdc++.h>
#define s size()
#define pb push_back
#define vl vector<long long>
typedef long long ll;
using namespace std;
vl mul(vl &a,vl &b)
{
ll lena=a.s;
ll lenb=b.s;
vl c(lena+lenb,0);
for(int i=0;i<lena;i++)
for(int j=0;j<lenb;j++) c[i+j]+=a[i]*b[j];
ll lenc=c.s;
for(int i=0,t=0;i<lenc;i++)
{
t+=c[i];
c[i]=t%10;
t/=10;
}
while(c.s>1&&c.back()==0) c.pop_back();
return c;
}
int main()
{
string A,B;
vl a,b,c;
cin>>A>>B;
ll lena=A.s;
ll lenb=B.s;
for(int i=lena-1;i>=0;i--) a.pb(A[i]-'0');
for(int i=lenb-1;i>=0;i--) b.pb(B[i]-'0');
c=mul(a,b);
ll lenc=c.s;
for(int i=lenc-1;i>=0;i--) cout<<c[i];
cout<<endl;
return 0;
}
也是实现手算乘法，用法比较巧妙，建议全文背诵/doge
高精度除法
只贴高精度除低精度，高精度除高精度很麻烦，而且比赛都是会取模的
#include<bits/stdc++.h>
#define s size()
#define pb push_back
#define vl vector<long long>
typedef long long ll;
using namespace std;
vl div(vl &a,ll b,ll &r)
{
vl c;
ll lena=a.s;
r=0;
for(int i=lena-1;i>=0;i--)
{
r=r*10+a[i];
c.pb(r/b);
r=r%b;
}
reverse(c.begin(),c.end());
while(c.s>1&&c.back()==0) c.pop_back();
return c;
}
int main()
{
string A;
ll b;
vl a,c;
ll r;
cin>>A>>b;
ll lena=A.s;
for(int i=lena-1;i>=0;i--) a.pb(A[i]-'0');
c=div(a,b,r);
ll lenc=c.s;
for(int i=lenc-1;i>=0;i--) cout<<c[i];
cout<<endl<<r<<endl;
return 0;
}
其中由于除法是从最高位运算的，要使与其他三个互通，函数里面用了reverse函数调换了位置，时间复杂度有点大，但是方便融合
四个高精度完毕
