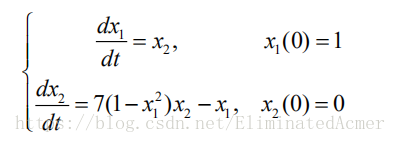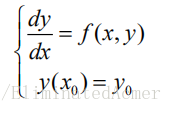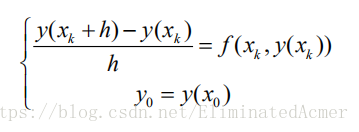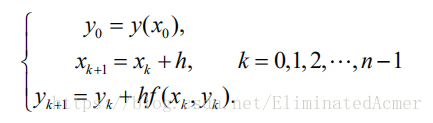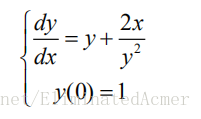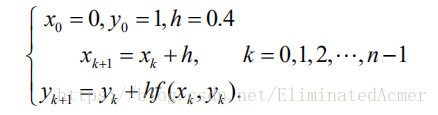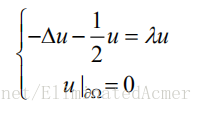17 级数求和
symsum(u,n,a,b)的功能是计算级数和。其中u是包含符号变量n的表达式,是待求和级数的通项。a为变量n的起始量,b为n的最终量
r=taylor(f,n,x,a). 该命令的功能是将符号函数f展开成(x-a)的n-1阶泰勒多项式。其中x是待展开的符号变量,其缺省值为最接近x的字母。
syms n ; symsum(1/(2*n-1),n,1,10) -------------------------------- ans = 31037876/14549535
18 求解常微分方程
1.在 Matlab 中,用大写字母 D 表示导数,Dy 表示 y 关于自变量的一阶导数,D2y 表示 y 关于自变量的二阶导数,依此类推.函数 dsolve 用来解决常微分方程(组)的求解问题,调用格式为
X=dsolve(‘eqn1’,’eqn2’,…)
如果没有初始条件,则求出通解,如果有初始条件,则求出特解
系统缺省的自变量为 t。
2.函数 dsolve 求解的是常微分方程的精确解法,也称为常微分方程的符号解.但是,有大量的常微分方程虽然从理论上讲,其解是存在的,但我们却无法求出其解析解,此时,我们需要寻求方程的数值解,在求常微分方程数值解方面,MATLAB 具有丰富的函数,将其统称为 solver,其一般格式为:
[T,Y]=solver(odefun,tspan,y0)
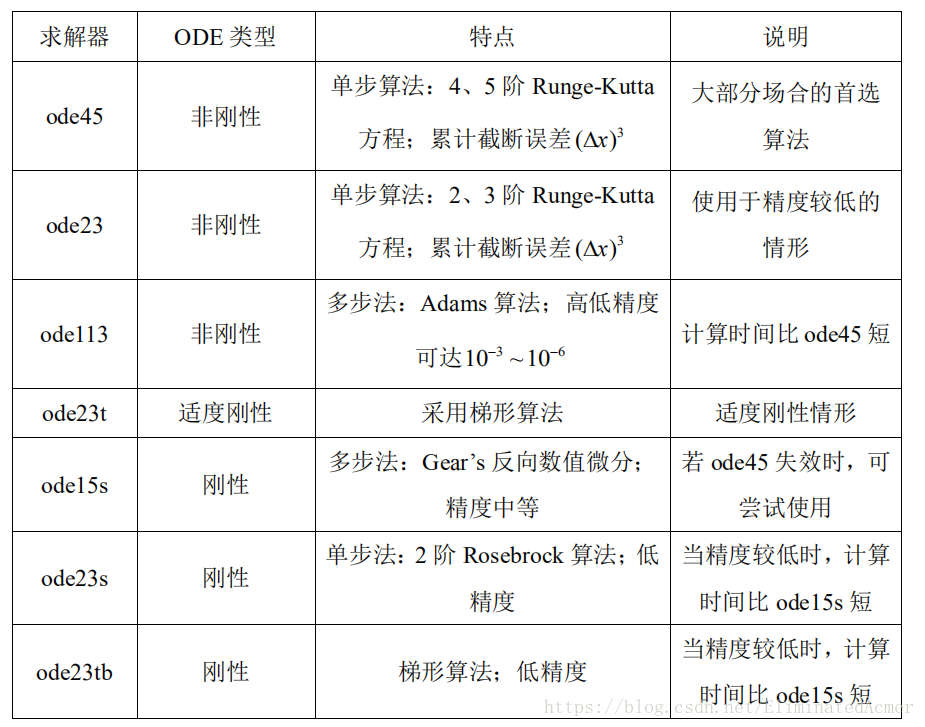
说明:(1)solver 为命令 ode45、ode23、ode113、ode15s、ode23s、ode23t、ode23tb、ode15i 之一.
(2)odefun 是显示微分方程 y ' = f (t , y) 在积分区间 tspan = [t 0 , t f ] 上从 t0 到 t f 用初始条件 y0 求解.
(3)如果要获得微分方程问题在其他指定时间点 t 0 , t1 , t 2 , , t f 上的解,则令tspan = [t 0 , t1 , t 2 , t f ] (要求是单调的).
(4)因为没有一种算法可以有效的解决所有的 ODE 问题,为此,Matlab 提供了多种求解器 solver,对于不同的 ODE 问题,采用不同的 solver
3.在 matlab 命令窗口、程序或函数中创建局部函数时,可用内联函数 inline,inline 函数形式相当于编写 M 函数文件,但不需编写 M-文件就可以描述出某种数学关系.调用 inline 函数,只能由一个 matlab 表达式组成,并且只能返回一个变量,不允许[u,v]这种向量形式.因而,任何要求逻辑运算或乘法运算以求得最终结果的场合,都不能应用 inline 函数,inline 函数的一般形式为:
FunctionName=inline(‘函数内容’, ‘所有自变量列表’)
例如:(求解 F(x)=x^2*cos(a*x)-b ,a,b 是标量;x 是向量 )在命令窗口输入:
Fofx=inline('x.^2.*cos(a.*x)-b','x','a','b');g = Fofx([pi/3 pi/3.5],4,1)
系统输出为:g=-1.5483 -1.7259注意:由于使用内联对象函数 inline 不需要另外建立 m 文件,所有使用比较方便,另外在使用 ode45 函数的时候,定义函数往往需要编辑一个 m 文件来单独定义,这样不便于管理文件,这里可以使用 inline 来定义函数。
例子:
一、ex(求精确解):
1. 求解微分方程 y ' + 2xy = xe-x2
syms x y; y=dsolve('Dy+2*x*y=x*exp(-x^2)','x')
运行结果:
2. 求微分方程 xy ' + y - e x = 0 在初始条件 y (1) = 2e 下的特解并画出解函数的图形.
syms x y; y=dsolve('x*Dy+y-exp(1)=0','y(1)=2*exp(1)','x');ezplot(y)
运行结果:
3. 求解微分方程组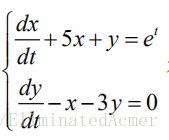
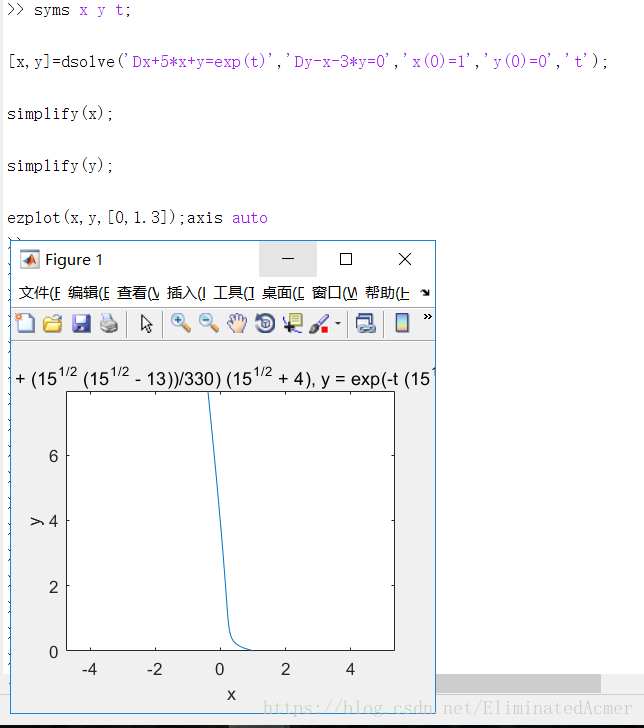
syms x y t;
[x,y]=dsolve('Dx+5*x+y=exp(t)','Dy-x-3*y=0','x(0)=1','y(0)=0','t');
simplify(x);
simplify(y);
ezplot(x,y,[0,1.3]);axis auto
其中,simplify函数可以对符号表达式进行简化。以下是运行结果:
二、ex(近似解):
1. 求解微分方程初值问题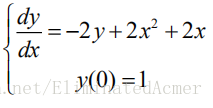
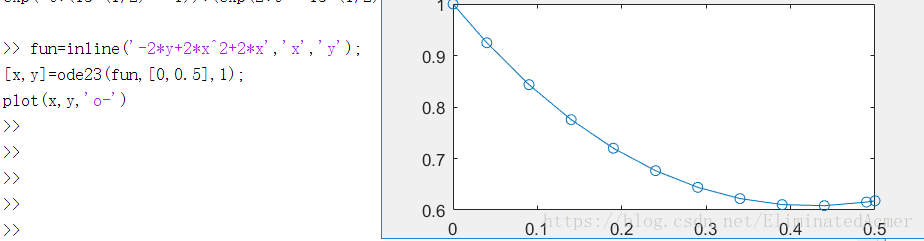
fun=inline('-2*y+2*x^2+2*x','x','y');
[x,y]=ode23(fun,[0,0.5],1);
plot(x,y,'o-')
2.求解微分方程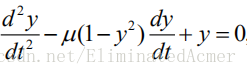
通过变换,将二阶方程化为一阶方程组求解.令,则
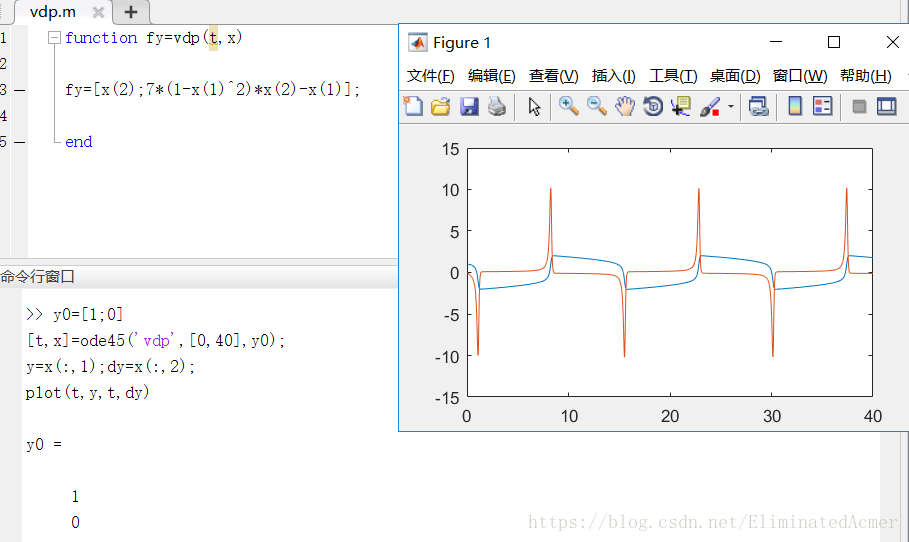
编写 vdp.m 文件:
function fy=vdp(t,x) fy=[x(2);7*(1-x(1)^2)*x(2)-x(1)]; end
命令行输入:
y0=[1;0]
[t,x]=ode45('vdp',[0,40],y0);
y=x(:,1);dy=x(:,2);
plot(t,y,t,dy)
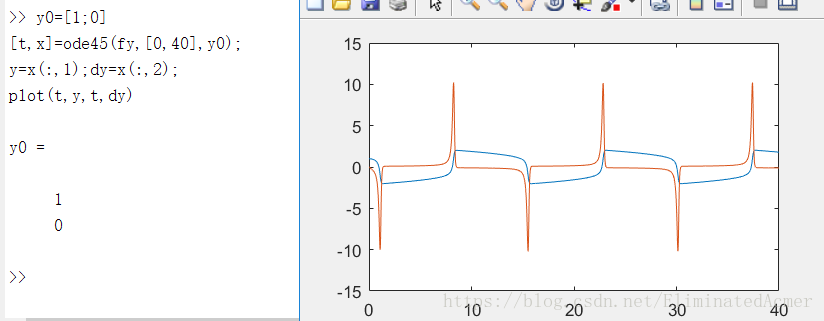
在使用ode45函数的时候,定义函数往往需要编辑一个 .m文件来单独定义,这样不便于管理文件,因此编写 inline 函数:
fy=inline('[x(2);7*(1-x(1)^2)*x(2)-x(1)]','t','x')
运行:
结果一致!
三、ex(用 Euler 折线法求解):
Euler 折线法求解的基本思想是将微分方程初值问题
化成一个代数(差分)方程,主要步骤是用差商替代微商
,于是
记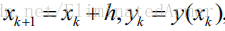
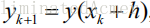
1. 用 Euler 折线法求解微分方程初值问题
的数值解(步长h取 0.4),求解范围为区间[0,2]
本题的差分方程为:
clear;
f=sym('y+2*x/y^2');a=0;b=2;
h=0.4;
n=(b-a)/h+1;
x=0;
y=1;
szj=[x,y];%数值解
for i=1:n-1
y=y+h*subs(f,{'x','y'},{x,y});%subs,替换函数
x=x+h;
szj=[szj;x,y];
end;
szj;
plot(szj(:,1),szj(:,2))
说明:替换函数 subs 例如:输入 subs(a+b,a,4) 意思就是把 a 用 4 替换掉,返回 4+b,也可以替换多个变量,例如:subs(cos(a)+sin(b),{a,b},[sym('alpha'),2])分别用字符 alpha 替换 a 和 2 替换 b,返回 cos(alpha)+sin(2)。
偏微分方程解法
Matlab 提供了两种方法解决 PDE 问题,一是使用 pdepe 函数,它可以求解一般的 PDEs,具有较大的通用性,但只支持命令形式调用;二是使用 PDE 工具箱,可以求解特殊 PDE 问题,PDEtoll 有较大的局限性,比如只能求解二阶 PDE问题,并且不能解决片微分方程组,但是它提供了 GUI 界面,从复杂的编程中解脱出来,同时还可以通过 File—>Save As 直接生成 M 代码.
实例:
求解一个正方形区域上的特征值问题:
正方形区域为:。
(1)使用 PDE 工具箱打开 GUI 求解方程
(2)进入 Draw 模式,绘制一个矩形,然后双击矩形,在弹出的对话框中设置Left=-1,Bottom=-1,Width=2,Height=2,确认并关闭对话框
(3)进入 Boundary 模式,边界条件采用 Dirichlet 条件的默认值
(4)进入 PDE 模式,单击工具栏 PDE 按钮,在弹出的对话框中方程类型选择Eigenmodes,参数设置 c=1,a=-1/2,d=1,确认后关闭对话框
(5)单击工具栏的 D 按钮,对正方形区域进行初始网格剖分,然后再对网格进一步细化剖分一次
(6)点开 solve 菜单,单击 Parameters 选项,在弹出的对话框中设置特征值区域为[-20,20]
(7)单击 Plot 菜单的 Parameters 项,在弹出的对话框中选中 Color、Height(3-D plot)和 show mesh 项,然后单击 Done 确认
(8)单击工具栏的“=”按钮,开始求解
得到结果:
s=dsolve('D2y+4*Dy+29*y=0','y(0)=0','Dy(0)=15','x')
----------------------------------------------------------------
s =
3*sin(5*x)*exp(-2*x)
[x,y,z]=dsolve('Dx=2*x-3*y+3*z','Dy=4*x-5*y+3*z','Dz=4*x-4*y+2*z','t')
x=simplify(x)
y=simplify(y)
z=simplify(z)
------------------------------------------
x =
exp(-t)*(C13 + C15*exp(3*t))
y =
exp(-2*t)*(C14 + C13*exp(t) + C15*exp(4*t))
z =
exp(-2*t)*(C14 + C15*exp(4*t))