本文主要介绍matlab中求解常微分方程(组)的dsolve和ode系列函数,并通过例子加深读者的理解。
一、符号介绍
D: 微分符号;D2表示二阶微分,D3表示三阶微分,以此类推。
二、函数功能介绍及例程
1、dsolve 函数
dsolve函数用于求常微分方程组的精确解,也称为常微分方程的符号解。如果没有初始条件或边界条件,则求出通解;如果有,则求出特解。
1)函数格式
Y = dsolve(‘eq1,eq2,…’ , ’cond1,cond2,…’ , ’Name’)
其中,‘eq1,eq2,…’:表示微分方程或微分方程组;
’cond1,cond2,…’:表示初始条件或边界条件;
‘Name’:表示变量。没有指定变量时,matlab默认的变量为t;
2)例程
例1.1(dsolve 求解微分方程)
求解微分方程:
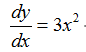
dsolve('Dy=3*x^2','x')
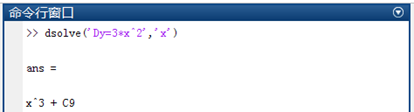
例1.2(加上初始条件)
求解微分方程:

例2(dsolve 求解微分方程组)
求解微分方程组:
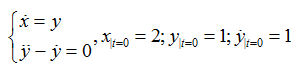
由于x,y均为t的导数,所以不需要在末尾添加’t’。

2、ode函数
在上文中我们介绍了dsolve函数。但有大量的常微分方程,虽然从理论上讲,其解是存在的,但我们却无法求出其解析解,此时,我们需要寻求方程的数值解。
ode是Matlab专门用于解微分方程的功能函数。该求解器有变步长(variable-step)和定步长(fixed-step)两种类型。不同类型有着不同的求解器,具体说明如下图。
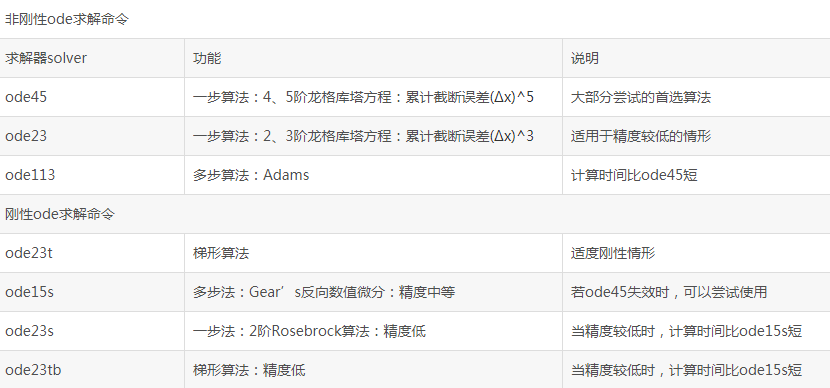
其中,ode45求解器属于变步长的一种,采用Runge-Kutta算法;其他采用相同算法的变步长求解器还有ode23。ode45表示采用四阶-五阶Runge-Kutta算法,它用4阶方法提供候选解,5阶方法控制误差,是一种自适应步长(变步长)的常微分方程数值解法,其整体截断误差为(Δx)^5。解决的是Nonstiff(非刚性)常微分方程。
ode45是解决数值解问题的首选方法,若长时间没结果,应该就是刚性的,可换用ode15s试试。
下面将以ode45为例具体介绍函数的使用方法。
1)函数格式
[T,Y] = ode45(‘odefun’,tspan,y0)
[T,Y] = ode45(‘odefun’,tspan,y0,options)
[T,Y,TE,YE,IE] = ode45(‘odefun’,tspan,y0,options)
sol = ode45(‘odefun’,[t0 tf],y0...)
其中: odefun是函数句柄,可以是函数文件名,匿名函数句柄或内联函数名;
tspan 是求解区间 [t0 tf],或者一系列散点[t0,t1,...,tf];
y0 是初始值向量
T 返回列向量的时间点
Y 返回对应T的求解列向量
options 是求解参数设置,可以用odeset在计算前设定误差,输出参数,事件等
TE 事件发生时间
YE 事件发生时之答案
IE 事件函数消失时之指针i
2)微分方程标准化
利用ode45求解高阶微分方程时,需要做变量替换。下面说明替换的基本思路。
微分方程为

初始条件
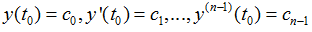
首先做变量替换
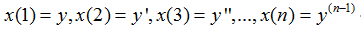
原微分方程可以转换为下面的微分方程组的格式:
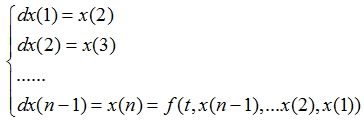
下面就可以利用转换好的微分方程组来编写odefun函数。
3)例程
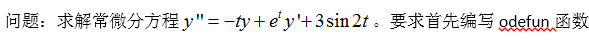
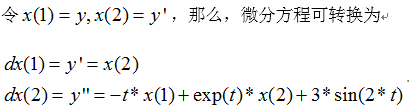
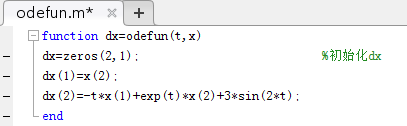
在matlab中新建脚本文件,编写函数如下:

 浙公网安备 33010602011771号
浙公网安备 33010602011771号