matlab练习之矩阵分析与处理

 

 

•  3范数

L₁ 范数（列和范数）norm(A,1)

L₂ 范数（列和范数）norm(A,2)

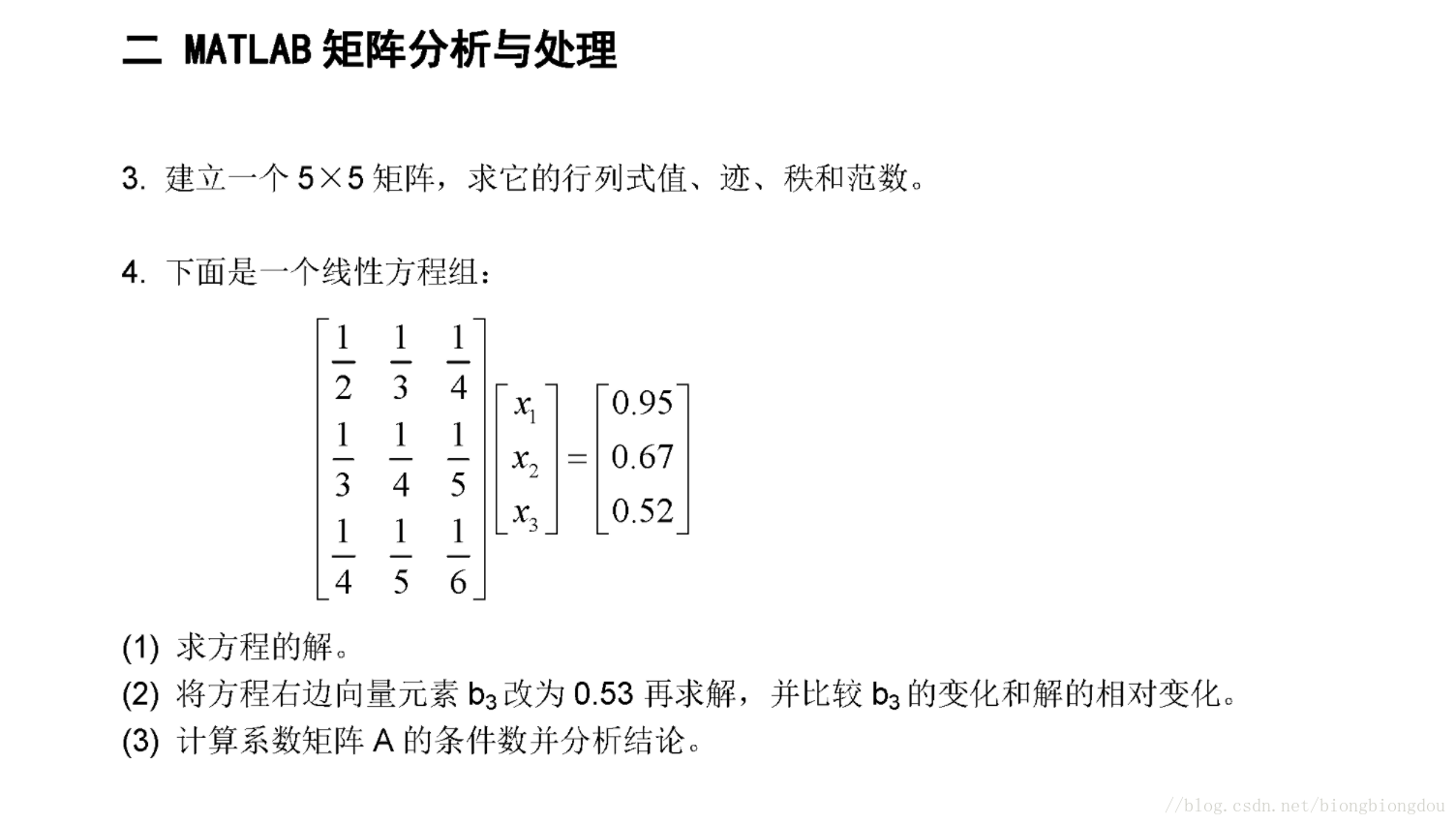
A=rand(5,5);
A1=rank(A)%秩
A2=trace(A)%迹 
A3=det(A)%行列式
A4=norm(A,2)%2范数
------------------------------------
A1 =
     5
A2 =
    2.8203
A3 =
    0.0538
A4 =
    2.6379

• 4.1

全页折叠

X = linsolve(A,B)

X = linsolve(A,B,opts)

[X,r] = linsolve(___)

X = linsolve(A,B) 使用以下方法之一求解线性方程组 AX = B：

• 当 A 是方阵时，linsolve 使用 LU 分解和部分主元消元法。

• 对于所有其他情况，linsolve 使用 QR 分解和列主元消元法。

如果 A 为病态（对于方阵）或秩亏（对于矩形矩阵），则 linsolve 发出警告。

X = linsolve(A,B,opts) 使用由 options 结构体 opts 确定的合适的求解器。opts 中的字段是说明矩阵 A 的属性的逻辑值。例如，如果 A 是上三角矩阵，您可以设置 opts.UT = true 以使 linsolve 使用为上三角矩阵设计的求解器。linsolve 不再测试验证 A 是否具有 opts 中指定的属性。

[X,r] = linsolve(___) 还返回 r，即 A 的条件数的倒数（对于方阵）或 A 的秩（对于矩形矩阵）。您可以使用上述语法中的任何输入参数组合。使用此语法时，如果 A 为病态或秩亏，linsolve 不会发出警告。

A=[1/2 1/3 1/4;1/3 1/4 1/5;1/4 1/5 11/6];
B=[0.95;0.67;0.52];
X = linsolve(A,B)
---------------------------------------------
X =

    1.0202
    1.3193
    0.0006
---------------------------------------------
b3=0.53后
A=[1/2 1/3 1/4;1/3 1/4 1/5;1/4 1/5 11/6];
B=[0.95;0.67;0.53];
X = linsolve(A,B)
cond（A）
---------------------------------------------
X =

    1.0220
    1.3121
    0.0066

ans =102.5850