python递归函数

python递归函数

1. 关于递归

　　　　程序调用自身的编程技巧称为递归（ recursion）。

　　　　递归作为一种算法在程序设计语言中广泛应用。

　　　　一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，

　　　　它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，

　　　　递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，

　　　　大大地减少了程序的代码量。

　　　　递归的能力在于用有限的语句来定义对象的无限集合。

　　　　一般来说，递归需要有边界条件、递归前进段和递归返回段。

　　　　当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

 

 

 

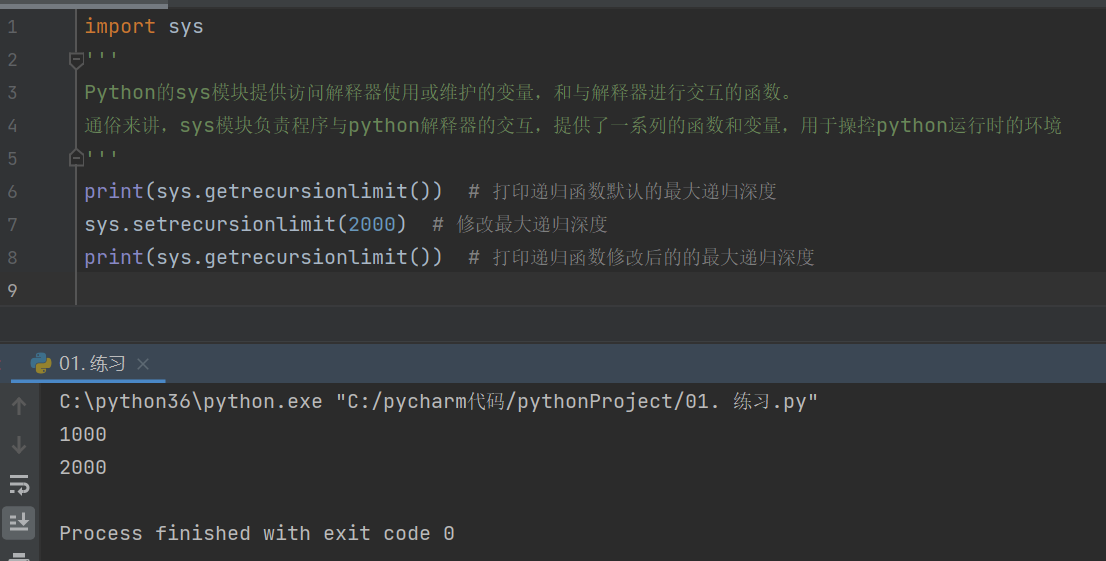
在计算机中，函数调用时通过栈(stack)这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。

由于栈的大小不是无限的，所以，递归调用的次数过多，就会导致栈溢出。

 

 递归的特点

1. 必须有一个明确的结束条件，要不就会变成死循环了，最终撑爆系统
2. 每次进入更深一层递归时，问题规模相比上次递归都应有所减少
3. 递归执行效率不高，递归层次过多会导致栈溢出

 

 

 

 

2. 使用递归打印斐波那契数列

 代码

def recur_fibo(n):
    """递归函数
    输出斐波那契数列"""
    if n <= 1:
        return n
    else:
        return (recur_fibo(n - 1) + recur_fibo(n - 2))

# 获取用户输入
nterms = int(input("您要输出几项? "))
# 检查输入的数字是否正确
if nterms <= 0:
    print("输入正数")
else:
    print("斐波那契数列:", end='')
    for i in range(nterms):
        print(recur_fibo(i), end=' ')

 结果

 3. 二分查找

 

 

 

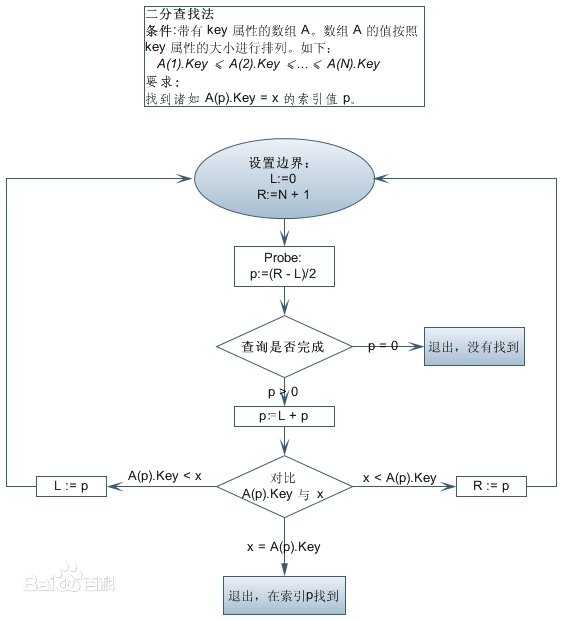
 l = [11, 23, 43, 57, 68, 76, 81, 99, 123, 321, 432, 567, 666, 712, 899, 999, 1111]

 1 """
二分法能够使用的场景  数据集必须有序
"""
def my_partner(target_num, l):  # target_num=321  l=l
    if len(l) == 0:
        print('不好意思 我尽力 没找到')
        return
    # 先获取中间位置索引值
    middle_index = len(l) // 2  # 8
    # 判断中间索引对应的值比目标值大还是小
    if target_num > l[middle_index]:
        # 说明要找的元素只可能出现在列表的右侧
        l_right = l[middle_index + 1:]  # l[9:]
        print(l_right)
        my_partner(target_num, l_right)
    elif target_num < l[middle_index]:
        # 说明要找的元素只可能出现在列表的左侧
        l_left = l[:middle_index]
        print(l_left)
        my_partner(target_num, l_left)
    else:
        print('找到了', target_num)
# my_partner(444, l)  找不到 需要添加结束条件
# my_partner(11, l)  # 要查找的元素在开头  那么还没有依次查找的效率高