Z 算法/拓展 KMP 详解

更好的阅读体验

引入

先来看几个问题：

什么是 Z 算法呢？

Z 算法（Z-Algorithm，又叫拓展 KMP 或 exKMP）是一种字符串匹配算法，可以在 \(O(n)\) 时间内算出一些关于字符串匹配的问题。

为什么要用 Z 算法？

暴力进行匹配是 \(O(n^2)\) 的，但用 Z 后是 \(O(n)\) 的（KMP 也可以实现类似的功能）。

接下来是一些约定：

1. \(s[l .. r]\) 表示 \(s_ls_{l + 1}s_{l + 2} ... s_r\)
2. z 函数用 \(z()\) 表示，原字符串用 \(s\) 表示
3. 下标从 \(1\) 开始

算法流程

定义

定义： 对于任意 \(i(2 \le i \le n)\)，定义 \(z(i)\) 表示满足 \(s[1 .. x] = s[i .. i + x - 1]\) 的最大的 \(x\)。

例如：
\(s = \texttt{aabbaabb}\)，\(z(5) = 4\)，因为 \(s[1 .. 4] = s[5 .. 8]\)
\(s = \texttt{aabab}\)，\(z(3) = 0\)
\(s = \texttt{ababa}\)，\(z(3) = 3\)

并且，对于任意 \(i(2 \le i \le n)\)，我们把区间 \([i, i + z(i) - 1]\) 叫做一个 Z-Box，共有 \(n\) 个 Z-Box。
这个概念有什么用呢？一会求 Z 函数时会用到。

如何求解

求 \(z[1 .. n]\) 的总复杂度是 \(O(n)\) 的。

我们知道暴力求 \(z\) 是 \(O(n^2)\)的，那么为了优化复杂度，我们需要用之前算出的 \(z[2 .. i - 1]\) 来算出 \(z(i)\)。

我们维护右端点最右的 Z-Box 的左右端点，记为 \(zl\), \(zr\)。（初始都为 \(0\)）

考虑如何求 \(z(i)\)。如果 \(zr < i\)，那么我们并无法利用之前的 \(z\)，所以直接暴力更新 \(z(i)\)，并更新 \(zl\), \(zr\)。下面讨论 \(zr \ge i\) 的情况。

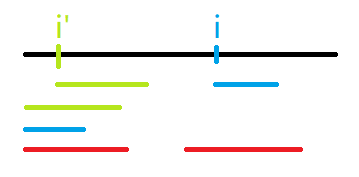
令 \(i' = i - zl + 1\)，图中绿色是 \(i'\) 的 Z-Box 和 \(s\) 与之长度相等的前缀，由 \(z\) 函数定义得两段绿色相等。蓝色同理。两段红色是 \([zl, zr]\) 和 \(s\) 与之长度相等的前缀，两段红色也相等。

由图可知，\(z(i) >= \min{z(i'), zr - i + 1}\)。

那么如果 \(z(i') < zr - i + 1\)，那么直接让 \(z(i) = z(i')\)。

但是如果 \(z(i') \ge zr - i + 1\) 呢？是不是让 \(z(i) = zr - i + 1\) 就好了呢？

其实不一定，看下面这张图：

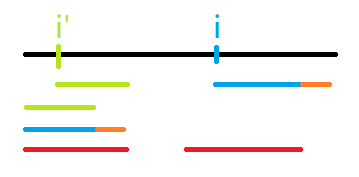
图中 \(zr - i + 1\) 应该等于蓝色，但是实际上 \(z(i)\) 应该是蓝色+橙色，所以这种情况我们直接在 \(zr - i + 1\) 的基础上暴力更新 \(z(i)\)，并更新 \(zl, zr\)。

无关紧要的证明：

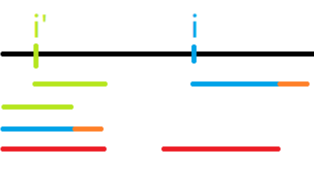
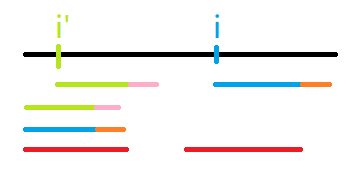
其实 \(z(i')\) 不可能大于 \(zr - i + 1\)，因为如果大于，那么就会变成下面这样：

那么粉色和橙色的前面部分是相等的，那么红色就可以继续往后延伸，与前面 \(z\) 的定义矛盾。

时间复杂度

因为 \(zl\), \(zr\) 一直往右移动，不移动 \(zl, zr\) 时的操作为常数，所以时间复杂度为 \(O(n)\)。

代码

int z[N];
void z_algorithm(const char *s) { // 下标从 1 开始
	int l = 0, r = 0;
	int n = strlen(s + 1);
	for(int i = 2; i <= n; i++) {
		if(i <= r) z[i] = std::min(z[i - l + 1], r - i + 1);
		while(i + z[i] <= n && s[i + z[i]] == s[z[i] + 1]) z[i]++;
		if(i + z[i] > r) l = i, r = i + z[i] - 1;
	}
}

应用

例题 1

给出两个字符串 s, t，求出所有的位置 x，满足 \(s[x .. x + len(t) - 1] = t\)。
其中 \(len(s), len(t) \le 10^5\)，s, t 仅包含大小写字母。

可以设一个字符 \(r = t + \texttt{!} + s\)，然后对 \(r\) 跑一边 Z-Algorithm。
然后看 \(r[len(t) + 2 .. len(r)]\) 中有多少个的 Z 函数等于 \(len(t)\)。

也可以按照 Z 算法类似的方式直接算。（设 \(e(i)\) 表示满足 \(s[i .. i + x - 1] = t[1 .. x]\) 的最大的 \(x\)）

int e[N];
void exkmp(const char *s, const char *t) { // 下标从 1 开始
	int l = 0, r = 0;
	int n = strlen(s + 1);
	for(int i = 2; i <= n; i++) {
		if(i <= r) e[i] = std::min(z[i - l + 1], r - i + 1);
		while(i + e[i] <= n && s[i + e[i]] == t[e[i] + 1]) e[i]++;
		if(i + e[i] > r) l = i, r = i + e[i] - 1;
	}
}

例题 2

洛谷 P5410

#include <cstdio>
#include <algorithm>
#include <cstring>

typedef long long LL;

const int N = 2e7 + 5;

char a[N], b[N];

int z[N];
void z_algorithm(const char *s) { // 下标从 1 开始
	int l = 0, r = 0;
	int n = strlen(s + 1);
	for(int i = 2; i <= n; i++) {
		if(i <= r) z[i] = std::min(z[i - l + 1], r - i + 1);
		while(i + z[i] <= n && s[i + z[i]] == s[z[i] + 1]) z[i]++;
		if(i + z[i] > r) l = i, r = i + z[i] - 1;
	}
}

int e[N];
void exkmp(const char *s, const char *t) { // 下标从 1 开始
	int l = 0, r = 0;
	int n = strlen(s + 1);
	for(int i = 2; i <= n; i++) {
		if(i <= r) e[i] = std::min(z[i - l + 1], r - i + 1);
		while(i + e[i] <= n && s[i + e[i]] == t[e[i] + 1]) e[i]++;
		if(i + e[i] > r) l = i, r = i + e[i] - 1;
	}
}

int main() {
	scanf("%s%s", a + 1, b + 1);
	int la = strlen(a + 1), lb = strlen(b + 1);
	z_algorithm(b);
	z[1] = lb;
	LL ans = 0;
	for(int i = 1; i <= lb; i++) ans ^= (LL)i * (z[i] + 1);
	printf("%lld\n", ans);
	exkmp(a, b);
	for(int i = 1; i <= lb; i++) if(a[i] == b[i]) e[1] = i; else break;
	ans = 0;
	for(int i = 1; i <= la; i++) ans ^= (LL)(i) * (e[i] + 1);
	printf("%lld\n", ans);
	return 0;
}