后缀数组详解
后缀数组是一类可以巧妙转化问题的字符串算法。
前置知识
一些约定
- 字符串下标从 \(1\) 开始
- 字符串 \(t\) 长度为 \(len(t)\)。特别的，字符串 \(s\) 长度为 \(n\)
- 本文中假设字符串只包含 小写字母
- \(s[l..r]\) 表示 \(s_ls_{l+1}\ldots s_r\)
- 后缀 \(i\) 表示 \(s[i..n]\)
- 排名 \(i\) 后缀 表示所有后缀中字典序排名为 \(i\) 的那个的开始位置
后缀数组
什么是后缀数组
后缀数组，顾名思义，就是存了后缀的数组。
其实后缀数组就是把所有后缀放在一起，然后按字典序排序。
盗一张 OI Wiki 的图。
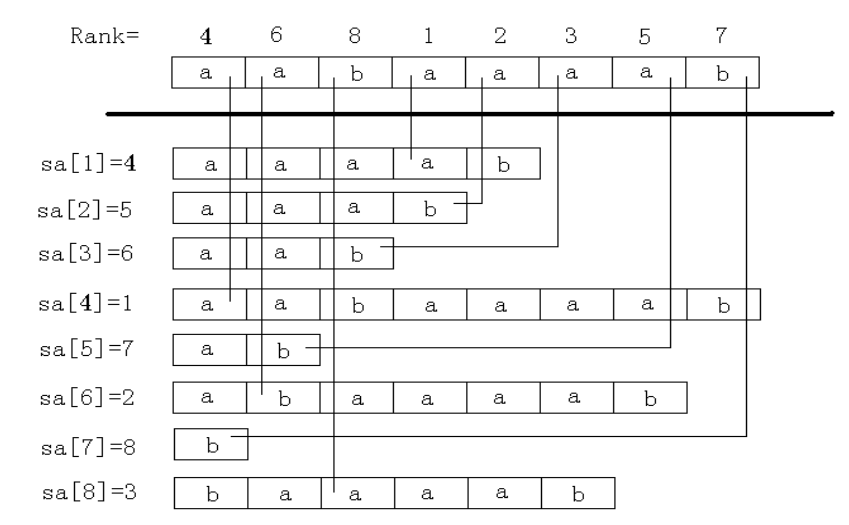
后缀数组求法
求后缀数组的方法很多，比如说 \(O(n^2 \log n)\) 暴力，或者 \(O(n \log^2 n)\) 哈希，还有两种 \(O(n)\) 做法（SA-IS，DC3，链接来自 OI Wiki 推荐），以及本文要讲的 倍增算法。
算法思想
暴力的想法是，首先我们比较每个后缀 \(i\) 的第 \(1\) 个字符，然后比较第 \(2\) 个，然后第 \(3\) 个……一直到第 \(n\) 个。但这样是 \(O(n^2)\) 的。
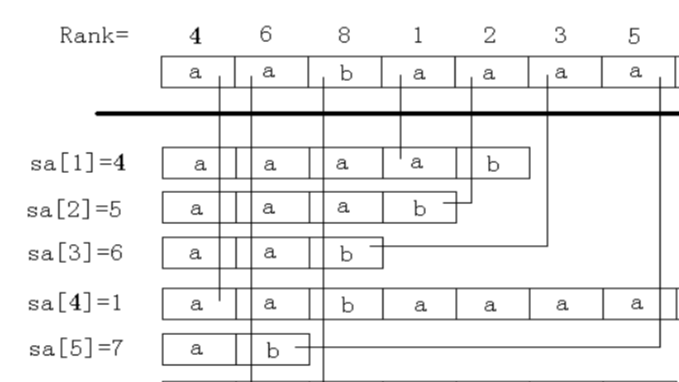
那怎么优化它呢？别忘了我们的算法叫倍增啊！当我们对一个后缀 \(i\) 的前 \(w\) 位排完序时，后缀 \(i\) 的后面 \(w\) 位的顺序我们也是知道的！这时我们只需要对于后缀 \(i\) 中前 \(w\) 位的排名和后缀 \(i\) 中 \([w + 1 .. 2w]\) 位的排名进行双关键字排序，就可以得到后缀 \(i\) 中前 \(2w\) 位的排名啦！
再盗一张 OI Wiki 的图
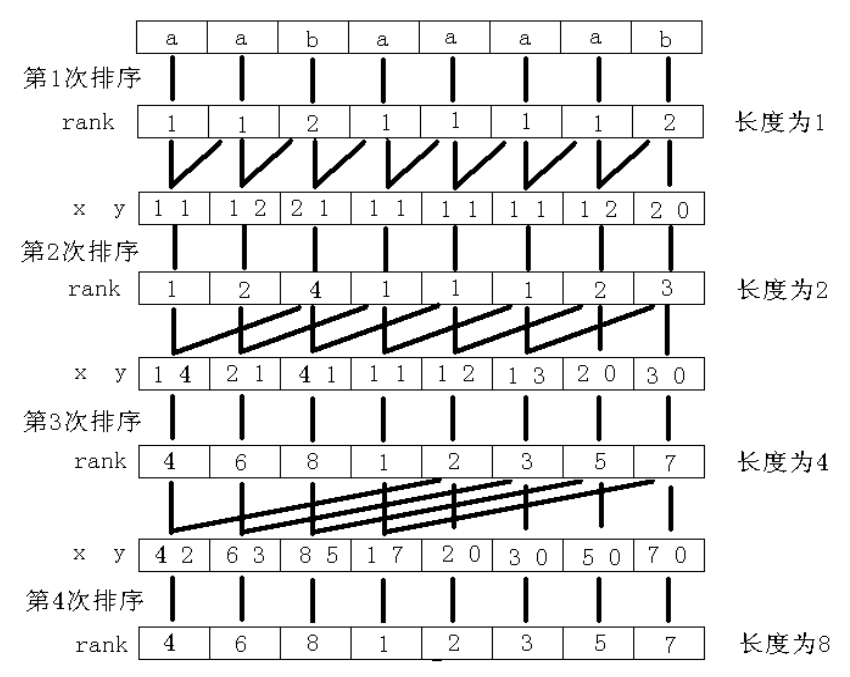
具体实现
如果不想看 TLE 代码，可以直接移步到 优化实现，前面的内容是为优化实现作铺垫的。
变量约定
sa[i]— 排名 \(i\) 后缀的开始位置rk[i]— 后缀 \(i\) 的排名tp[i]— 即 temp，辅助数组，具体意思下面会说p— 辅助变量，具体意思下面会说
sort 实现
现在我们可以写出代码啦！每次暴力更新第一、二关键字，用 sort 排序就好啦！
代码来自 OI Wiki，变量大致是一样的（其实是我懒）
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1000010;
char s[N];
int n, w, sa[N], rk[N << 1], oldrk[N << 1];
// 为了防止访问 rk[i+w] 导致数组越界，开两倍数组。
// 当然也可以在访问前判断是否越界，但直接开两倍数组方便一些。
int main() {
int i, p;
scanf("%s", s + 1);
n = strlen(s + 1);
for (i = 1; i <= n; ++i) sa[i] = i, rk[i] = s[i];
for (w = 1; w < n; w <<= 1) {
sort(sa + 1, sa + n + 1, [](int x, int y) {
return rk[x] == rk[y] ? rk[x + w] < rk[y + w] : rk[x] < rk[y];
}); // 这里用到了 lambda
memcpy(oldrk, rk, sizeof(rk));
// 由于计算 rk 的时候原来的 rk 会被覆盖，要先复制一份
for (p = 0, i = 1; i <= n; ++i) {
if (oldrk[sa[i]] == oldrk[sa[i - 1]] &&
oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]) {
rk[sa[i]] = p;
} else {
rk[sa[i]] = ++p;
} // 若两个子串相同，它们对应的 rk 也需要相同，所以要去重
}
}
for (i = 1; i <= n; ++i) printf("%d ", sa[i]);
return 0;
}
这样我们就可以 AC 了！
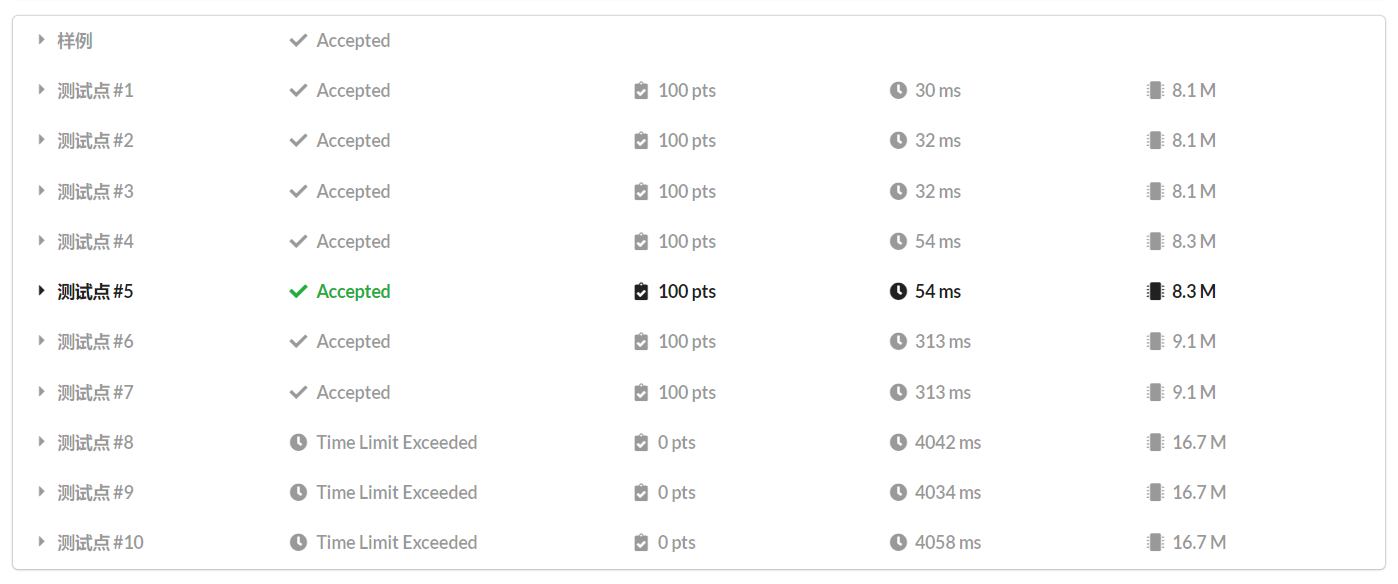
好打脸！
算啦，常数才不是我们要管的事，加 O2 不就能过了。
但是！这样算法不就成 \(O(n \log^2 n)\) 的了？我们的 优秀 算法怎么能允许这样的事出现？
基数排序实现
要让算法的复杂度为 \(O(n \log n)\)，就要在排序上下功夫。
双关键字排序，我们可以用基数排序（其中稳定排序使用计数排序）！
于是，排序复杂度降为 \(O(n \log n)\)。
再次盗用 OI Wiki 的代码
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1000010;
char s[N];
int n, sa[N], rk[N << 1], oldrk[N << 1], id[N], cnt[N];
int main() {
int i, m, p, w;
scanf("%s", s + 1);
n = strlen(s + 1);
m = max(n, 300);
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1; w < n; w <<= 1) {
memset(cnt, 0, sizeof(cnt));
for (i = 1; i <= n; ++i) id[i] = sa[i];
for (i = 1; i <= n; ++i) ++cnt[rk[id[i] + w]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[id[i] + w]]--] = id[i];
memset(cnt, 0, sizeof(cnt));
for (i = 1; i <= n; ++i) id[i] = sa[i];
for (i = 1; i <= n; ++i) ++cnt[rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[id[i]]]--] = id[i];
memcpy(oldrk, rk, sizeof(rk));
for (p = 0, i = 1; i <= n; ++i) {
if (oldrk[sa[i]] == oldrk[sa[i - 1]] &&
oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]) {
rk[sa[i]] = p;
} else {
rk[sa[i]] = ++p;
}
}
}
for (i = 1; i <= n; ++i) printf("%d ", sa[i]);
return 0;
}
这下终于可以 AC 了。
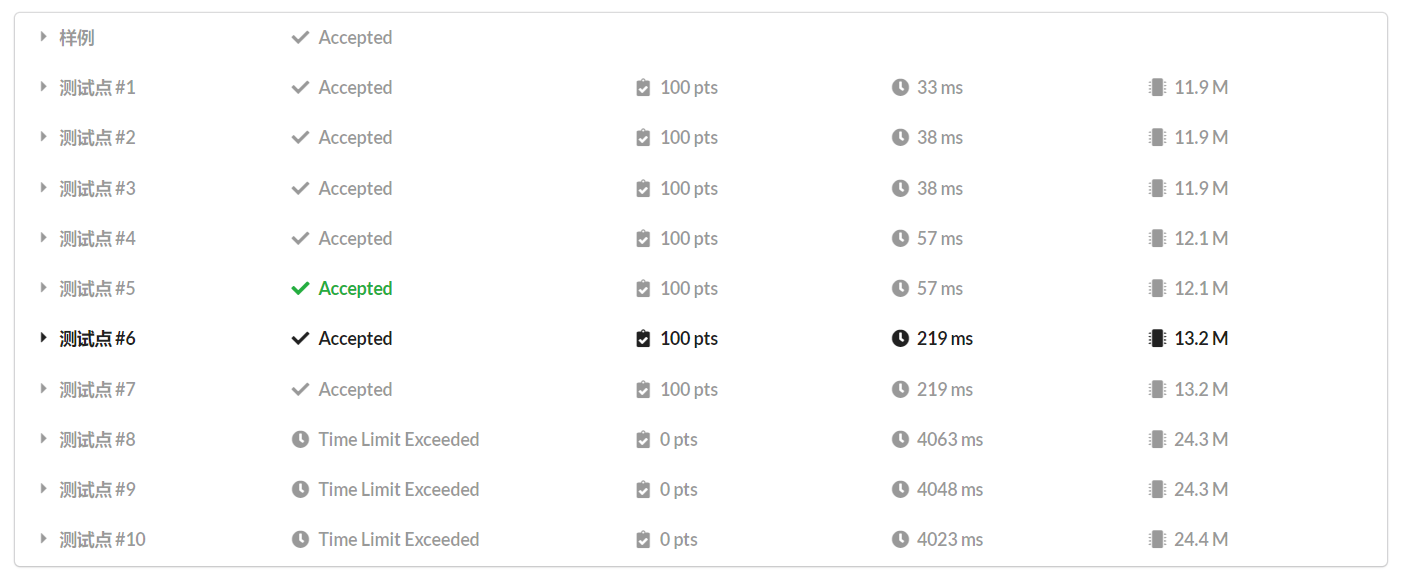
打脸第二次
为什么！明明复杂度是正确的！
但是，这份代码的常数确实太大了。
优化实现
其实，基数排序中第二关键字可以不用计数排序，而是直接在存入时就排好序。
这里用我的代码详细讲解。（终于不是 OI Wiki 了）
// main code
const int N = 1e6 + 5;
char s[N];
int n, m;
// sa 和 rk 开两倍的原因是有可能访问越界，当然也可以判越界
// tot 用于计数排序
int sa[N << 1], rk[N << 1], tot[N], tp[N];
void Sort() { // 计数排序并处理出 sa
for(int j = 0; j <= m; j++) tot[j] = 0; // 桶清零
for(int j = 1; j <= n; j++) tot[rk[j]]++;
for(int j = 0; j <= m; j++) tot[j] += tot[j - 1]; // 计数排序套路
for(int j = n; j >= 1; j--) sa[tot[rk[tp[j]]]--] = tp[j];
}
void SA() {
m = 'z';
for(int j = 1; j <= n; j++) rk[j] = s[j], tp[j] = j;
Sort(); // 由于下面不会用到 rk，所以不用处理 rk，当然处理了也没错
for(int i = 1, p = 0; p < n; i <<= 1, m = p) { // i 即上文的 w
p = 0;
for(int j = 1; j <= i; j++) tp[++p] = n - i + j;
for(int j = 1; j <= n; j++) if(sa[j] > i) tp[++p] = sa[j] - i;
Sort();
for(int j = 1; j <= n; j++) tp[j] = rk[j]; // 由于 tp 不会再用到，我们用 tp 来表示上一轮的 rk
rk[sa[1]] = p = 1;
for(int j = 2; j <= n; j++)
rk[sa[j]] = ((tp[sa[j - 1]] == tp[sa[j]] && tp[sa[j - 1] + i] == tp[sa[j] + i]) ? p : ++p);
}
}
这一部分比较复杂，下面是详细讲解。
第一部分
// Code 1.1 (main code, Line 10~25)
void Sort() { // 计数排序并处理出 sa
for(int j = 0; j <= m; j++) tot[j] = 0; // 桶清零
for(int j = 1; j <= n; j++) tot[rk[j]]++;
for(int j = 0; j <= m; j++) tot[j] += tot[j - 1]; // 计数排序套路
for(int j = n; j >= 1; j--) sa[tot[rk[tp[j]]]--] = tp[j];
}
首先来看计数排序。计数排序的这里的作用是对第一关键字作稳定排序。下面分句看。
for(int j = 1; j <= n; j++) tot[rk[j]]++; // Code 1.1, Line 4
这里将所有的后缀 \(i\) 的排名记录到桶里。注意此时 rk 有可能相同，但排到最后肯定是不同的（因为长度都不同）。
for(int j = n; j >= 1; j--) sa[tot[rk[tp[j]]]--] = tp[j]; // Code 1.1, Line 6
这里更新 sa，先说一下此时每个数组的意思。
tp[i]— 第二关键字排名为 \(i\) 的后缀的开始位置（至于为什么不直接记录后缀 \(i\) 的第二关键字，到后面就懂了）rk[i]— 上一轮排完后后缀 \(i\) 的排名，此处是后缀 \(i\) 的第一关键字。
那么这句话就是枚举 第二关键字的排名 \(j\)，那么 tp[j] 就是当前枚举的（第二关键字排名为 \(j\) 的）字符串的开头，又因为 sa[i] 表示排名 \(i\) 后缀的开头，所以这句话就是说：
将当前枚举字符串的 tot 作为这个字符串的排名，并将 tot 自减（tot 自减是计数排序的套路）。
注意到需要的是稳定排序，所以枚举是倒序的。
第二部分
// Code 1.2 (main code, Line 20)
for(int i = 1, p = 0; p < n; i <<= 1, m = p) // i 即上文的 w
这里的 \(p\) 指的是已经排出的不同后缀的个数。
第三部分
// Code 1.3 (main code, Line 21~23)
p = 0;
for(int j = 1; j <= i; j++) tp[++p] = n - i + j;
for(int j = 1; j <= n; j++) if(sa[j] > i) tp[++p] = sa[j] - i;
这一部分是对第二关键字进行排序，也就是更新 tp。
这里 sa 就是原来的意思，tp 还是表示第二关键字排名为 \(i\) 的后缀的开始位置。
for(int j = 1; j <= i; j++) tp[++p] = n - i + j; // Code 1.3, Line 3
这里是将后缀 \(n - i + 1 .. n\) 进行排序，对于这些后缀，它们是没有第 \(i + 1 .. 2i\) 位的，所以要单独处理。
当然，对于这部分，长度越小排名越前。
for(int j = 1; j <= n; j++) if(sa[j] > i) tp[++p] = sa[j] - i; // Code 1.3, Line 4
这一部分是对那些剩下的后缀（即后缀 \(1 .. n - i\)）排序，这里可以理解为我们在枚举 sa[j]，即按第一次的排名枚举后缀。实际上，我们枚举的是剩下后缀的第 \(i+1\) 位，即第二关键字开始的位。所以这里就是说：
按上次的排名枚举后缀 \(j\)，并将后缀 \(j - i\) 作为第 \(p\) 小的字符串，并将 \(p\) 自增。
第四部分
// Code 1.4 (main code, Line 26~28)
rk[sa[1]] = p = 1;
for(int j = 2; j <= n; j++)
rk[sa[j]] = ((tp[sa[j - 1]] == tp[sa[j]] && tp[sa[j - 1] + i] == tp[sa[j] + i]) ? p : ++p);
这里是对 \(rk\) 进行更新。此时各个数组的意义：
rk[i]— 这一轮后缀 \(i\) 的排名sa[i]— 这一轮排名 \(i\) 后缀开始的位置tp[i]— 上一轮后缀 \(i\) 的排名- \(p\) — 已经排出的不同排名个
这一部分就一起解释吧。
第 2 行将排名 \(1\) 后缀的排名和 \(p\) 置为 \(1\)。（其实此时 \(p\) 还是计数器，不过计数完了就成了不同排名个数）
然后比较相邻两个字符串（用上一轮的 \(rk\) 进行比较），不同将排名个数 \(p\) 加一。
压行实现
不讲。
const int N = 1e6 + 5;
char s[N];
int n, m;
int sa[N << 1], rk[N << 1], tot[N], tp[N];
void calcSA() {
m = 'z';
for(int i = 0, p = 0; p < n; i = (i ? i << 1 : 1), m = p) {
if(i) {
p = 0;
for(int j = 1; j <= i; j++) tp[++p] = n - i + j;
for(int j = 1; j <= n; j++) if(sa[j] > i) tp[++p] = sa[j] - i;
} else for(int j = 1; j <= n; j++) rk[j] = s[j], tp[j] = j;
for(int j = 0; j <= m; j++) tot[j] = 0;
for(int j = 1; j <= n; j++) tot[rk[j]]++;
for(int j = 0; j <= m; j++) tot[j] += tot[j - 1];
for(int j = n; j >= 1; j--) sa[tot[rk[tp[j]]]--] = tp[j];
if(!i) continue;
for(int j = 1; j <= n; j++) tp[j] = rk[j];
rk[sa[1]] = p = 1;
for(int j = 2; j <= n; j++)
rk[sa[j]] = ((tp[sa[j - 1]] == tp[sa[j]] && tp[sa[j - 1] + i] == tp[sa[j] + i]) ? p : ++p);
}
}
height 数组
定义
LCP 定义
\(lcp(s, t)\) 表示字符串 \(s\) 和 \(t\) 的最长公共前缀，也即最大的 \(i\) 满足 \(s[1..i]=t[1..i]\)。
height 数组定义
\(height[i] = lcp(sa[i], sa[i - 1])\)，即 \(height[i]\) 表示排名 \(i\) 和 \(i - 1\) 后缀的 LCP。
引理
引理：\(height[rk[i]] \ge height[rk[i - 1]] - 1\)，即后缀 \(i\) 和排名前一位的后缀的LCP 不小于 后缀 \(i\) 排名前一位的和前两位的LCP \(-1\)。
证明：（我不会证我懒，所以找了 OI Wiki 的证明 怎么又是 OI Wiki）
代码实现
void get_height() { // ht[] 就是 height
for(int i = 1, k = 0; i <= n; i++) {
if(rk[i] == 1) { ht[rk[i]] = 0; continue; }
if(k) k--;
int j = sa[rk[i] - 1];
while(i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
ht[rk[i]] = k;
}
}
