树状数组详解

更好的阅读体验

树状数组详解

引入

先问几个问题。

什么是线段树？

线段树是一种数据结构，支持 \(\log\) 级别的区间修改查询操作。

为什么要有线段树？

用数组实现区间查询、区间修改是 \(O(n)\) 的，但用树状数组是 \(O(\log n)\)。

树状数组和线段树的对比？

1. 名字不一样
2. 两个都是 \(\log\) 级数据结构
3. 树状数组支持区间查询，区间修改，但线段树支持基本上所有区间操作（\(\log n\) 时间）
4. 树状数组空间复杂度 \(n\)，常数小；线段树空间复杂度 \(4n\)，常数较大。

树状数组原理介绍

前置芝士

位运算

大意：
按位与：在二进制中对每一位进行对应操作：1&1=1, 1&0=0, 0&1=0, 0&0=0

二叉树

大意：
二叉树的定义：每个节点至多有 2 个儿子的树。

树状数组原理

首先上一张二叉树的图：（为了方便将节点右对齐）

图片来源：https://www.cnblogs.com/xenny/p/9739600.html，已经过博主同意，下同。

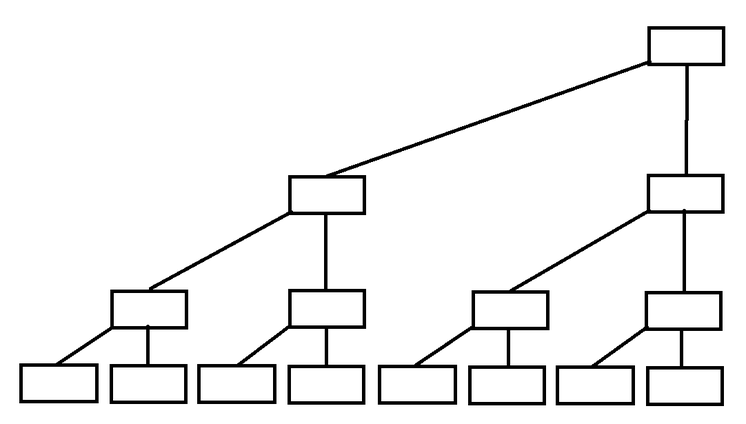
是不是看着有些熟悉呢？没错，这就是线段树。

但是树状数组可不长这样，前面说过它的空间复杂度是 \(n\)。
那树状数组是什么样呢？我们将每一列都只留最上面的节点，就变成了这样：

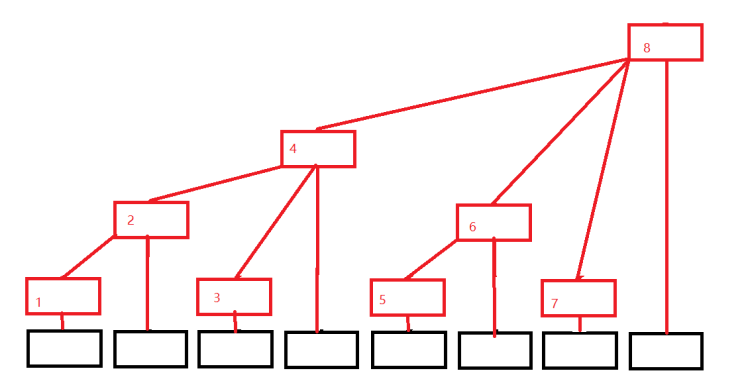
我们发现：（设原数组是 a[]，树状数组是 c[]）

c[1] = a[1]
c[2] = a[1] + a[2]
c[3] = a[3]
c[4] = a[1] + a[2] + a[3] + a[4]
c[5] = a[5]
c[6] = a[5] + a[6]
c[7] = a[7]
c[8] = a[1] + a[2] + a[3] + a[4] + a[5] + a[6] + a[7] + a[8]

找规律发现：\(c[i] = \sum_{j = i - lowbit(i) + 1}^i a_j\)

\(lowbit\) 原文中有描述，简单来说就是二进制下的从右往左第一个 \(1\) 的值，求法是 x & -x。

应用

说了这么多，树状数组到底是怎么维护区间的呢？

维护区间有四种，分别是：

• 单点修改，单点查询
• 单点修改，区间查询
• 区间修改，单点查询
• 区间修改，区间查询

下面来分别讲解。

单点修改，单点查询

传统数组即可。

单点修改，区间查询

再来看一下这个图：

发现

\[\sum_{i = 1}^k a_i = c(i) + c(i - lowbit(i)) + c(i - lowbit(i) - lowbit\left(i - lowbit(i)\right) + \cdots + c(1) \]

证明：

\[\begin{aligned} c(i) = &\sum_{k = i - lowbit(i) + 1}^i a_k\\ c(i - lowbit(i)) = &\sum_{k = i - lowbit(i) - lowbit(i - lowbit(i)) + 1}^{i - lowbit(i)} a_k\\ &\vdots\\ a(1) = &a_1 \end{aligned}\]

上面看不懂没关系，用代码也许好理解些：

int sum = 0, k;
while(k > 0) {
    sum += c[k];
    k -= lowbit(k);
}
// 此时 sum 值为 a[1] + a[2] + ... + a[k]

现在我们就解决了区间查询，但如何修改呢？
我们需要将包含 \(a_i\) 的 \(c\) 都修改，即：
\(c(i)\), \(c(i + lowbit(i))\), \(c(i + lowbit(i) + lowbit(i + lowbit(i)))\), \(\cdots\)
代码：

int add, k;
while(k <= n) {
    c[k] += add;
    k += lowbit(i);
}
// 此时已经将 a[k] += add 的修改加到树状数组中了

到此为止，我们就解决了区间查询，单点修改。

区间修改，单点查询

前置芝士

差分数组

大意：
设 \(t(i) = \sum_{j = 1}^i a_j\)
那么 \(a_i = \sum_{j = 1}^i t(j)\)

区间修改，单点查询原理

树状数组可以维护单点修改，区间查询，但如何实现区间修改，单点查询呢？

我们可以用维护 \(a\) 的差分数组，而不是 \(a\) 数组。
此时区间修改 \([l, r]\) 可以转化成 a[l] += add, a[r + 1] -= add，即单点修改；
单点查询 \(a_x\) 可以转化成询问 \([1, x]\) 的和，即区间查询。

完美！

区间修改，区间查询

仍然利用差分：

\[\begin{aligned} \sum_{i = 1}^k a_i &= (t(1)) + (t(1) + t(2)) + (t(1) + t(2) + t(3)) + \cdots + \sum_{i = 1}^k t(i)\\ &= \sum_{i = 1}^k \sum_{j = 1}^i a_j\\ &= \sum_{j = 1}^k \sum_{i = j}^k a_j\\ &= \sum_{j = 1}^k a_j \times (k - j + 1)\\ &= (k + 1) \sum_{j = 1}^k a_j - \sum_{j = 1}^k a_j \times j \end{aligned}\]

然后就可以维护两个树状数组，一个 \(a_i\)，一个 \(a_i \times i\)。

题目推荐

洛谷 P3374 代码
洛谷 P3368 代码

参考及图片来源： https://www.cnblogs.com/xenny/p/9739600.html
关于版权： 可以转载或以任何形式借用，但均需注明本文链接。（图片请注明上面的链接，不要注明这篇的）