论文信息:
Nichol A , Achiam J , Schulman J . On First-Order Meta-Learning Algorithms[J]. 2018.
摘要
文章从一个任务分布中抽取许多任务来训练元学习模型,使其可以更快的学习这个分布中未遇到的任务。
仅在元学习更新过程中仅使用一阶微分,就能得到在新任务上实现快速微调的参数初始化。
这里介绍两种算法:扩展FOMAML和Reptile。First-order MAML是一阶MAML,忽略了二阶导数得到MAML的近似值;Reptile从一个任务中重复采样训练,然后将初始化值移动到该任务的训练权重(??)
1、介绍
虽然机器学习在很多任务上已经超越了人类,但它们需要多得多的数据才能达到同样的性能。
人类不是从头开始学习,而是带着大量的先验知识进入任务,这些知识编码在大脑和DNA中。面对新任务,人类可能是微调或重新组合一些已有的技能。有研究者认为,人类的快速学习能力可以被解释为贝叶斯推理,具有人类学习速度的算法关键是让算法更加贝叶斯化。但是实际上,利用深度学习网络和现有计算能力开发贝叶斯机器学习算法是一个很大的挑战。
元学习出现成为一种小样本学习方法。不是试图模仿贝叶斯推理,这在计算上很难处理,而是试图用任务集直接优化快速学习算法。具体来说,众多任务构成一个分布,每个任务的训练集输入到算法中,算法快速生成一个agent,在任务的测试集上表现良好。
过去主要有两种方法:一种是将学习算法编码到循环网络的权值中,但测试时不执行梯度下降[8]。近期迸发出许多追随者,例如RL2。另一种是学习网络的初始化,在测试时对新任务进行微调。这种方法的一个典型实例是使用大型数据集如Imagenet进行与训练,然后在比较小的数据集上进行微调。然而经典的预训练方法不能保证学到一个适合于微调的初始化,而且需要一些特别的技巧以获得良好性能。最近MAML算法直接优化了与此初始化的性能,通过微调过程进行微分。即便接收样本外的数据,学习者也能落入一个对梯度敏感的学习算法,比RNN的泛化性能更好。但是MAML需要在优化的过程中进行微分,不适用于测试时需要执行大量gradient step的问题。MAML的作者提出了一种变体first-order MAML(FOMAML),忽略二阶导数项可用避免这个问题,但丢失了一些梯度信息。但是FOMAML在MiniImageNet数据集上的工作几乎与MAML一样好。有些工作预示通过梯度下降法进行微分时忽略二阶导数,没有不良影响。本文扩展这一观点,并探索基于一节梯度信息的元学习算法的潜力。
Contributions:
1、一阶MAML的实现比之前广泛认可的简单
2、引入Reptile,一种FOMAML密切相关的算法,实现起来同样简单。Reptile与联合训练非常相似,但它是一种元学习算法。与FOMAML不同的是,Reptile不需要对每个任务进行训练集和测试集的分割,这让它在某些情况下成为更自然的选择。它也跟以前的fast wights/ slow weights相关[7]。
3、提供了一个适应于一阶MAML和Reptile的理论分析,表明它们都优化了任务内部的泛化。
4、在Mini-ImageNet和Omniglot数据集上进行了实验评价
2、元学习一个初始化
MAML的优化问题:找到一个参数的初始集合Φ,对于随机采样的任务和相关损失,学习者可在k次更新后降低损失。U是从τ 中取数据对Φ进行k次更新。
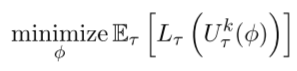
若A是训练集,B是测试集。MAML优化了泛化,类似于交叉验证。
![]()
其梯度下降计算:
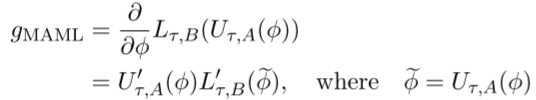
U‘是更新操作U的雅可比矩阵,FOMAML将这些梯度视为常量,及那个雅可比U‘替换为恒等操作。
![]()
MAML简化为:1、采样任务τ;2、更新参数输出φ;3、在更新后的参数φ上计算梯度(上式);4、将gFOMAML输入外循环。
3、Reptile
Reptile和MAML算法已有,对神经网络模型的参数进行初始化,当测试时优化这些参数,学习变得非常快!即从测试任务的少量示例中进行了概括。

在最后一步,将差值更新改为将该差值作为一个梯度放入自适应算法中,如Adam。具体形式可以是
![]()
其中α是SGD操作中的stepsize,并行算法如下:
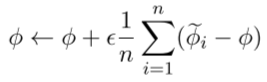
这种方法看起来很像期望损失的联合训练,事实上,如果U被定义为一阶梯度下降k=1,那么这种算法等同于期望损失的SGD
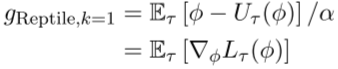
当k>1时,U的期望更新将不等于损失函数期望更新,而是将包含损失函数的二次甚至更高阶微分项,Reptile的收敛点与最小化E(L)不同。
除了stepsize的参数𝜖和任务采样外,Reptile的batch版本和SimuparallelSGD算法[21]相同,后者是一种通信效率高的分布式优化算法,比起标准平均梯度法,局部的梯度不经常平均参数。
4、一阶sin()曲线回归的例子
网络结构:MLP 1-64-64-1
5、理论分析
1、更新的leading order扩展
使用泰勒展开近似Reptile和MAML的更新,均含有同样的leading-order项:第一项最小化期望损失,第二项和更多感兴趣的项最大化任务内泛化能力。特别是,同任务不同minibatch间梯度的内积最大化。如果这个内积为正,一个batch内的梯度下降会改善另一个batch的性能。表达式定义,i为minibatch数,i∈[1,k]

k=2时,对三种算法的梯度更新进行泰勒展开:
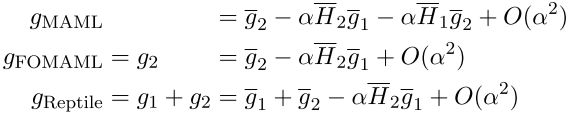

进行minibatch采样,求取三种算法梯度的期望,AvgGrad定义为期望损失的梯度,-AvgGrad使Φ向联合训练损失的最小方向迈进;AvgGradInner是梯度内积,-AvgGradInner是相同任务内不同batch梯度内积增加的方向,提升泛化能力。
k=2时,三种算法的梯度期望:

k≥2,三种算法的期望:
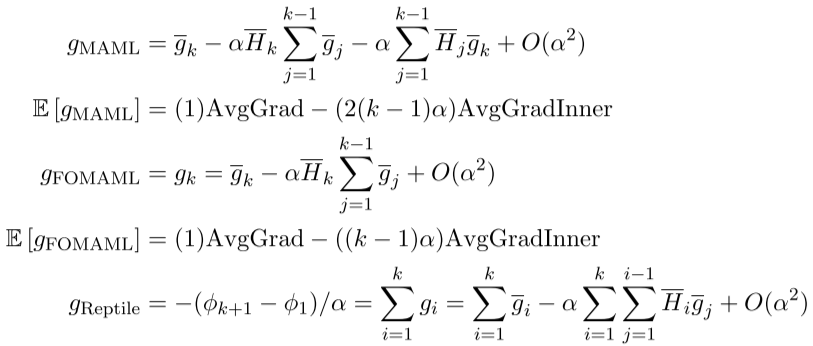
三者AvgGradInner和AvgGrad之间的系数比是:MAML>FOMAML>Retile. 这个比例与α和k正相关。
2、找到一个接近所有Solution Manifolds(解流形)的点

六、总结
本文提出一种新的算法Reptile,它的训练过程与联合训练只有细微区别,且只使用一阶梯度信息。文章给出Reptile工作原理的两种理论解释:
1、通过近似更新的泰勒级数,发现SGD自动给出了MAML计算的二阶项相同的项。这一项调整初始权重,以最大限度增加同一任务中不同小批梯度之间的点积,鼓励同任务小批量之间泛化梯度。
2、Reptile找到一个接近所有任务的最优解流形的点。
5.1的分析结果表明,在进行SGD时,MAML形式的更新过程自动包含其中,最大化不同小批量之间的泛化。这个结果部分解释了为什么微调(从ImageNet到更小的数据集)可以工作得更好。这一假设表明联合训练加微调将继续是元学习的一个强有力的基础。
参考文献:
⭕ 作者博客


 浙公网安备 33010602011771号
浙公网安备 33010602011771号