原文部分
摘要：
元学习算法与模型无关，兼容任何梯度下降训练的模型，适用于分类、回归和强化等。
元学习的目标是用大量任务训练一个模型，使它可以通过少量训练样本解决新的任务。
模型参数被显式训练，少量样本下少量梯度步长就能在新任务上产生良好的泛化性能。实际是将模型训练得易于微调。
亮点：1、小样本集的新任务；2、加速对梯度增强学习的微调
1、介绍
快速学习是一种人类智力：从几个例子中识别物体，或体验几分钟习得技能。为此AI的目标：从几个例子中快速学习和适应，并随着数据样本增加进一步调整。快速而灵活的学习是有挑战的，智能体需要整合鲜艳知识和少量新样本信息，同时避免新数据过拟合。先验和新数据的形式取决于任务，元学习机制应该对任务和完成任务的计算形式足够通用，以便获得最大实用性。
元学习算法于模型无关，可应用于被梯度下降训练的任何学习问题。这里的重点是深度神经网络，但修改后可以用于解决不同的架构和不同的问题。元学习中，训练模型的目标是从少量的新数据中快速学习新任务，被meta-learner训练的模型可以学习大量不同的任务。文章的核心思想是训练模型的初始化参数，使模型经过一次或几次梯度就能达到最佳性能。与之前的学习算法有所区别，Schmidhuber,1987; Bengio et al., 1992; Andrychowicz et al., 2016; Ravi & Larochelle, 2017，这些算法学习一个更新函数或者学习规则；Santoro et al., 2016要求recurrent，Koch, 2015要求Siamese network。文中算法的特点是：1、不增加学习的参数 2、不限制模型结构 3、可用多种损失函数（监督或者强化）。
从特征学习的角度，学习建立一个适用于多种任务的internal representation，只需要微调参数（例如主要调整前馈模型的顶层权重）就能取得很好的结果，事实上就是想要模型的初始化参数易于调整；从动态系统的角度，学习过程可以看作是最大化损失函数对于参数的灵敏度，灵敏度越高，局部参数的小变化可以大大改善任务损失。
2、算法
2.1 元学习问题定义
q(x1)和q(xt+1|xt,at)是什么？？
2.2 算法
Idea: 神经网络学习广泛适用于所有任务的内部特征，而不是单一任务。目标是找到对任务变化敏感的参数，对于任何任务，在损失梯度方向，参数很小的改变将对任务的损失函数有较大改进。
学习适用于所有任务的最佳参数：
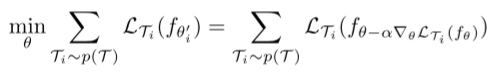
时刻记住：该方法旨在优化模型参数，使模型在新任务上使用很少的样本，通过少量梯度就能对任务产生最有效表现。
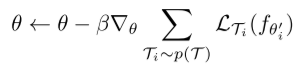
算法流程：
文章分析
MAML解决的问题是，对于F学到的f，规定f只负责决定参数的赋值方式，也就是模型的架构，参数的更新方式仍是提前固定，f为网络赋不同的初始值，这里为𝜙，最终输出网络参数θ。
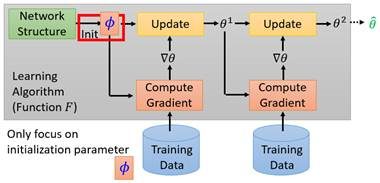
完全的元学习应该包括整个灰色框中的流程，但MAML只包含红色框中的一步，其他步骤依然人为设定。初始化的函数损失为：
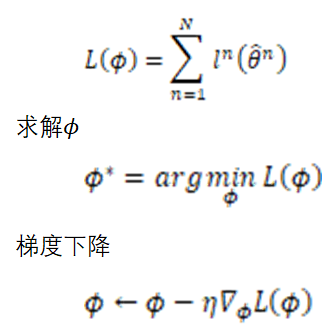
注意这里𝜙是要得到的初始化结果，θ是训练后的结果，作者的目的不是冲着最终结果，而是一个好的开始（经过几步下降得到最优）。
为了更快的计算，为简化梯度，作者做了两步调整：
1、θ只调整一次，认为达到最优，所以得到最优的𝜙代表了，经过𝜙下降一次的θ可以使所有任务的损失和最小。但实际测试中仍需要多次梯度。
2、从参考文献→文章详解中，可以看出作者试图省略二阶导数，最终梯度公式如下。
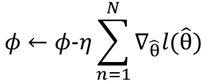
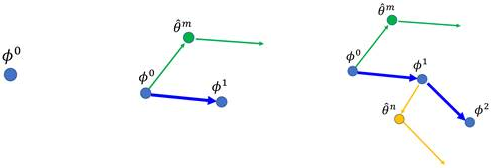
简化后的过程如图所示，先算一步得到θi（第i个任务），再算θi的梯度，θ跟随此梯度变化。
参考文献：
⭕ 代码实现
⭕ 文章翻译
⭕ 文章详解*
⭕ 作者详解
