Codeforces #198 Div2 题解

 

欢迎来到我的算法小屋

 

---

前言

简单描述文章的内容，结构，能够学到的知识点。

Problems
#	Name
A	The Wall
B	Maximal Area Quadrilateral
C	Tourist Problem
D	Bubble Sort Graph
E	Iahub and Permutations

 

 

A

题目描述

 

 题目的意思大致如下：

Iahub和他的朋友Floyd已经开始粉刷一面墙。Iahub把墙涂成红色，Floyd把墙涂成粉红色。可以认为这面墙是由非常多的砖头组成的，编号为1、2、3，以此类推。
Iahub的刷墙方案如下：

他跳过x-1块连续的砖，然后刷第x块砖。也就是说，他要把砖块x、2-x、3-x等涂成红色。同样地，弗洛伊德连续跳过y-1块砖，然后他画第y块。因此，他将把砖块y、2-y、3-y等涂成粉红色。
在刷了一整天的墙后，男孩们观察到有些砖头既被刷成了红色又被刷成了粉色。

男孩们想知道有多少块编号不小于a且不大于b的砖头既被涂成红色又被涂成粉色。这正是你的任务：计算并打印出问题的答案。

 

 

解题报告

A题还是蛮签到的了(只是我补题的时候做了半个小时，老蒟蒻了....)。

题目理解上应该半斤八两了，就是两人隔着一定数目的砖块粉刷，让后求既被刷成红色，又被刷成粉色的砖块编号。看完下面的样例解释，符合条件的是： "6、12、18"。此时给出的x = 2，y = 3和这三个数之间有太多关联了(doge)。2和3是"6、12、18"公有的因子。也就是说，这个符合条件的砖块编号，应该是2和3的公倍数，那么这个题现在就变成了，在a到b的范围中，有多少个最小公倍数。

 

参考代码(C++)

#include<bits/stdc++.h>

using namespace std;

#define INF 0x3f3f3f3f
#define N 520
#define mem(a,b) memset(a,b,sizeof(a))
typedef long long LL;
int T;


//最大公约数 gcd
LL gcd(LL a,LL b){

    return b?gcd(b,a%b):a;
}

//最小公倍数 lcm
LL lcm(LL a, LL b){
    return a*b/gcd(a,b);
}


void run(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
}

inline int read(){ 
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    } 
    return x*f;
}


int main(){
    run();

    LL x,y,a,b;
    cin >> x >> y >> a >> b;
    
    //算x，y的最小公倍数
    LL lcmxy = lcm(x,y);
    // LL gcdxy = gcd(x,y);
    // cout <<"gcdxy = " << gcdxy <<'\n'; //1
    // cout << "lcmxy=" << lcmxy <<'\n'; //6

    //-(a-1)/lcmxy这里相当于是扣除a之前存在的最小公倍数的数量，
    //因为范围是a-b，a之前的数据不需要计算，将其扣除
    cout <<(b/lcmxy - (a-1)/lcmxy);

    return 0;
}

 

要点总结

这里主要是回顾求最大公约数（gcd）和求最小公倍数（lcm）的算法模板。

 

B

题目描述

 

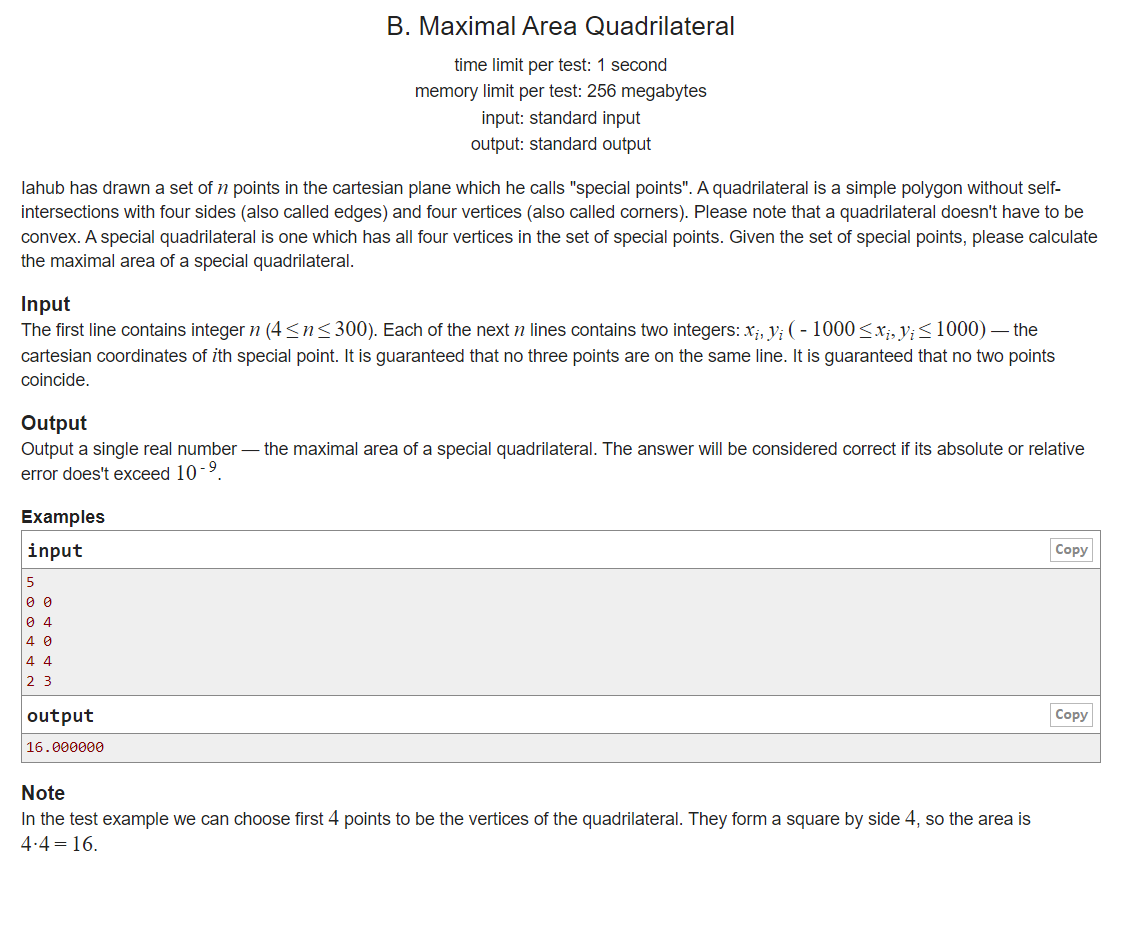
题目大致意思如下：

Iahub 在笛卡尔平面上绘制了一组 n 个点，他称之为“特殊点”。四边形是一个没有自相交的简单多边形，有四个边（也称为边）和四个顶点（也称为角）。请注意，四边形不一定是凸的。特殊四边形是在一组特殊点中具有所有四个顶点的四边形。给定一组特殊点，请计算特殊四边形的最大面积。

 

解题报告

B题可能有点离谱，通过人数和最后一题差不多

这个凹的还是凸的都不重要🤠，最最最核心的，就是让咱们定四个点，连接起来形成一个四边形，然后求这个四边形的最大面积。

想要计算三角形面积或者多边形的面积，那么，向量积(也可以说是叉积)就可以大展身手了。

 

向量积(叉积)计算三角形或多边形面积。

向量的数量积(点积、内积)理解。

 

 

向量的向量积(叉积)理解 + 理解计算四边形或者三角形面积

 

本题解决思路

知道了如何通过三个点形成的两个向量计算平行四边形以及三角形的面积，那么回到本题。我们可以先确定两个点，作为对角线，再去枚举数据，当做第三个点。

我们通过一根对角线将四边形划分为两个三角形的，一个称作上三角，一个称作下三角吧，到这里，

其实可以理解，咱们枚举第三个点的目的了，就是找出这个可以形成的三角形的最大面积，那么在一根公共边(对角线)下，最大的上三角+最大的下三角 = 最大的四边形面积。

 

参考代码(C++)

#include<bits/stdc++.h>

using namespace std;

#define inf 0x3f3f3f3f
#define N 310
#define mem(a,b) memset(a,b,sizeof(a))
typedef long long LL;
int n;

struct Pos{
    double x,y;
}p[N];

void run(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
}

inline int read(){ 
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    } 
    return x*f;
}

//计算三个坐标点形成的两个向量的向量积
double vect_product(Pos &a,Pos &b,Pos &c){
    double x1,y1,x2,y2;
     x1 = b.x - a.x;
     y1 = b.y - a.y;

     x2 = c.x - a.x;
     y2 = c.y - a.y;

     return (x1*y2 - x2*y1)/2.0;
}

int main(){
    run();

    //之前用了cin,但是没有使用cout来关闭同步流
    scanf("%d",&n);

    for(int i = 0;i < n;i++){
        double a,b;
        // cin >> a >> b;
        scanf("%lf %lf",&a,&b);
        p[i] = {a,b};
    }

    double upMax;
    double dwMax;
    double ansMax = -inf;
    for(int i = 0; i < n;i++){
        for(int j = 0; j < n;j++){
            if(i == j) continue;
            //枚举第三个点,开始求上三角形的最大值和下三角形的最大值
            upMax = -inf;
            dwMax = -inf;

            for(int k = 0; k < n;k++){
                if(i == k || j == k) continue;

                double ans = vect_product(p[i],p[j],p[k]);

                if(ans < 0) upMax = max(upMax,-ans);
                else dwMax = max(dwMax,ans);
            }

            //统计最大上+最大下的结果
            ansMax = max(ansMax,upMax + dwMax);
        }
    }

    printf("%.6lf\n",ansMax);
    return 0;
}

 

要点总结

积累用向量积解决多边形求面积的思路

  

 

 C

题目描述

题面翻译过来大致是这种的:

Iahub他在计划了一次旅行。在一条笔直的道路上有n个Iahub想去的目的地。

这n个目的地由非负整数序列a1, a2, ..., an描述。数字ak代表第k个目的地与起点的距离是ak公里。没有两个目的地位于同一个地方。
Iahub希望对每个目的地只访问一次。请注意，穿过一个目的地不算访问，除非Iahub明确地想在该点访问它。

另外，在Iahub访问完最后一个目的地后，他不会再回到0公里处，因为他在最后一个目的地停止了他的旅行。
位于x公里的目的地和位于y公里的下一个目的地之间的距离是|x-y|公里。我们称 "路线 "为访问目的地的顺序。

Iahub可以按照他想要的顺序访问目的地，只要他访问了所有的n个目的地，并且他不会访问一个目的地超过一次。
Iahub开始在纸上写出所有可能的路线，对于每一条路线，他都记下了他要走的总距离。

他感兴趣的是他选择一条路线所要走的平均公里数。

由于他对写出所有路线感到厌烦，他要求你帮助他。

 

解题报告

C题参考dalao的题解吧，暂时悟不透，不想磕...

C. Tourist Problem-爱代码爱编程 

D

题目描述

原题链接

 

 

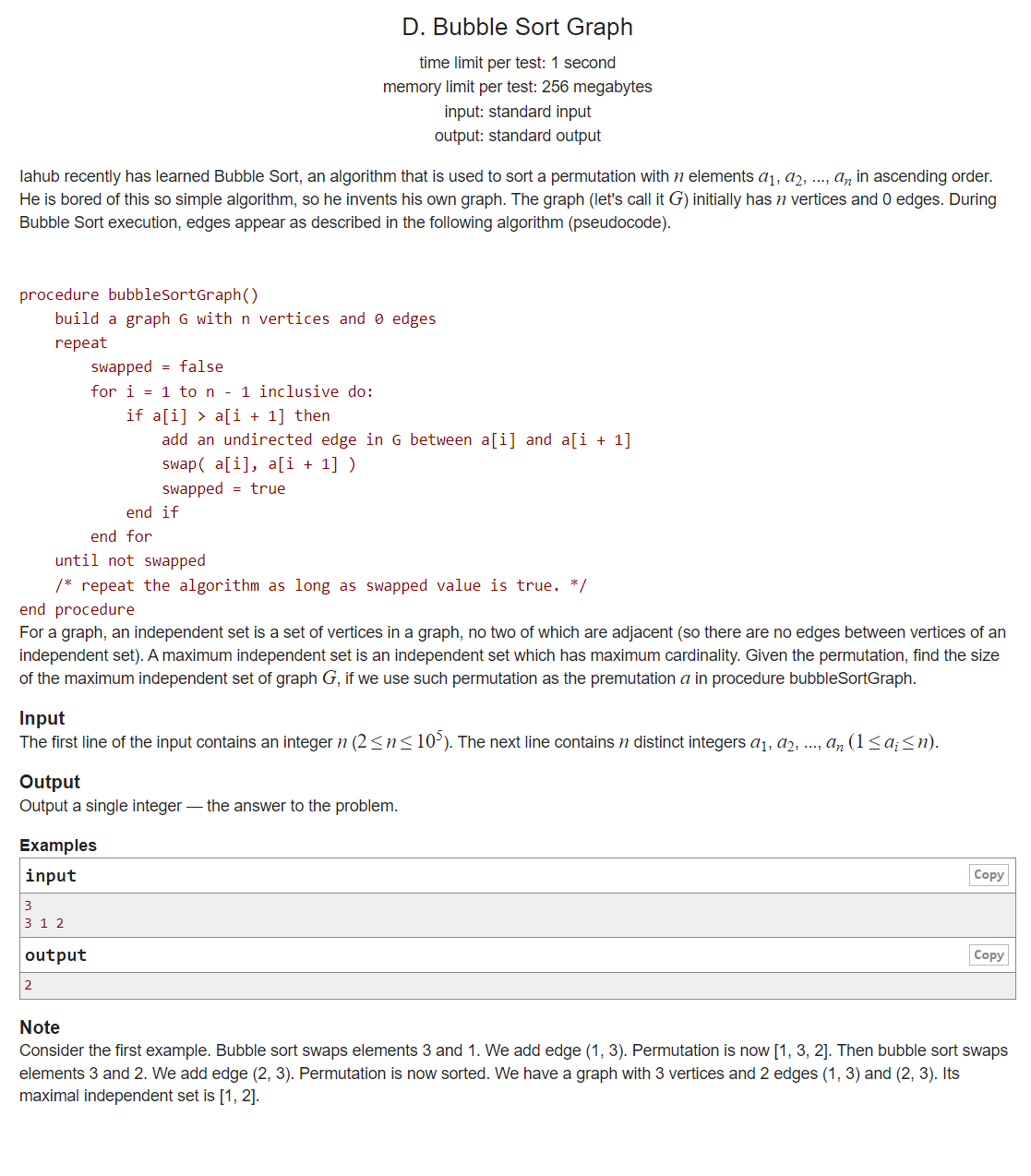
解题报告

这个题主要是要读懂题目的意思，其本质是一个最长上升子序列算法（需要二分优化）

 

题目的大致意思如下：

这位名叫Iahub 的朋友对冒泡排序进行了小小的改进，此时冒泡排序，在交换逆序对的时候，会在交换的这两个数之间建立一条边。

比如原本的序列是132，现在2和3需要交换，就会标记数字2的点和数字3的点存在一条边。

然后需要搞清楚，这个独立集是什么，题目中规定的独立集，用人话说出来就是，不存在彼此连通的边的顶点数量，

比如还是132举例子，数字1和数字2之间是没有建立任何边，那么数字1和数字2就构成了独立集，独立集的大小是2。

 

兜兜转转，逆序对要被交换成从小打到大排序的形式，那么就会建立边，什么情况的没有边了，原本就是按照从小到大形式排列的上升序列。

因此也就是求最长上升子序列（LIS）的长度，因为这个题的数据范围是10万，普通的LIS算法是$O(N^2)$的时间复杂度，所以需要二分来优化。

 

LIS算法学习参考

参考代码

//AcWing 896. 最长上升子序列 II
#include<bits/stdc++.h>

using namespace std;
/*宏定义*/
#define INF 0x3f3f3f3f
#define PI 3.141592653589793238462
#define N 100010 
#define x first
#define y second
typedef long long ll;
const double eps = 1e-8;
int n,cnt;
int a[N];
int f[N];//这个数组维护的是从左向右扫的过程中，严格单调递增的序列的数量


/*常用函数*/
//最大公约数
ll gcd(ll a,ll b) {return b==0 ? a : gcd(b,a%b);}
//最小公倍数
ll lcm(ll a,ll b) {return a*b / gcd(a,b);}
//快速幂
ll qmi(ll a,ll b,ll p) {ll ans = 1; while(b) { if(b & 1) ans = ans * a % p; a = a * a % p; b >>= 1; } return ans;}
//lowbit
int lowbit(int x) {return x & (-x);}


//cin 、 cout 优化
void run(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
}

//快读
inline int read(){ 
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    } 
    return x*f;
}

//二分查找 —— 在已经存储好的序列中，找到大于等于传入的参数x的元素的索引。
//然后因为这个数，违背了严格单调递增的规则，所以需要找到并替换到这个违背原则的数字
inline int find(int x){
    int l = 1,r = cnt;

    while(l < r){
        int mid = (l+r) >> 1;
        //注意画图理解
        if(f[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l;
}

int main(){
    run();

    cin >> n;
    for(int i = 1;i <= n;i++) cin >> a[i];

    // for(int i = 1;i <= n;i++) cout << a[i] <<' ';

    f[++cnt] = a[1];
    
    for(int i = 2;i <= n;i++){
        //假如在原本的序列中，能够放入f数组的，已经严格满足单调递增了，那直接放进去
        if(a[i] > f[cnt]) f[++ cnt] = a[i];
        //不满足严格单调递增
        else{
            //找到这个破坏了单调递增的家伙，给他替换了
            int temp_pos = find(a[i]);
            f[temp_pos] = a[i];
        }
    }


    cout << cnt;
    return 0;
}

 

要点总结

这种LIS算法是结合了栈的思想，比闫总的贪心要好理解一点。