蓝桥杯-AB路线(详细原创)
问题描述：
有一个由 N × M 个方格组成的迷宫，每个方格写有一个字母 A 或者 B。小蓝站在迷宫左上角的方格，目标是走到右下角的方格。他每一步可以移动到上下左右相邻的方格去。
由于特殊的原因，小蓝的路线必须先走 K 个 A 格子、再走 K 个 B 格子、再走 K 个 A 格子、再走 K 个 B 格子......如此反复交替。
请你计算小蓝最少需要走多少步，才能到达右下角方格? 注意路线经过的格子数不必一定是 K 的倍数，即最后一段 A 或 B 的格子可以不满 K 个。起点保证是 A 格子。
例如 K=3 时，以下 3 种路线是合法的:
AAA
AAAB
AAABBBAAABBB
以下 3 种路线不合法:
ABABAB
ABBBAAABBB
AAABBBBBBBAAA
输入格式
第一行包含三个整数 N、M 和 K。
以下 N 行，每行包含 M 个字符 ( A 或 B )，代表格子类型。
输出格式
一个整数，代表最少步数。如果无法到达右下角，输出 -1。
样例输入
4 4 2
AAAB
ABAB
BBAB
BAAA
样例输出
8
样例说明
每一步方向如下：下右下右上右下下；路线序列：AABBAABBA。
评测用例规模与约定
对于 20% 的数据，1 ≤ N, M ≤ 4。
对于另 20% 的数据，K=1。
对于 100% 的数据，1 ≤ N, M ≤ 1000，1 ≤ K ≤ 10。
题解:
宽搜bfs题, 用queue队列按要求搜索。
但需要注意 正常二维bfs搜索标记是否访问过的st数组用的二维, 但是这题用的st数组是三维
st含义:
st[x][y][z]: 坐标x, y上的字符, 在第z次访问的时候是否访问过了
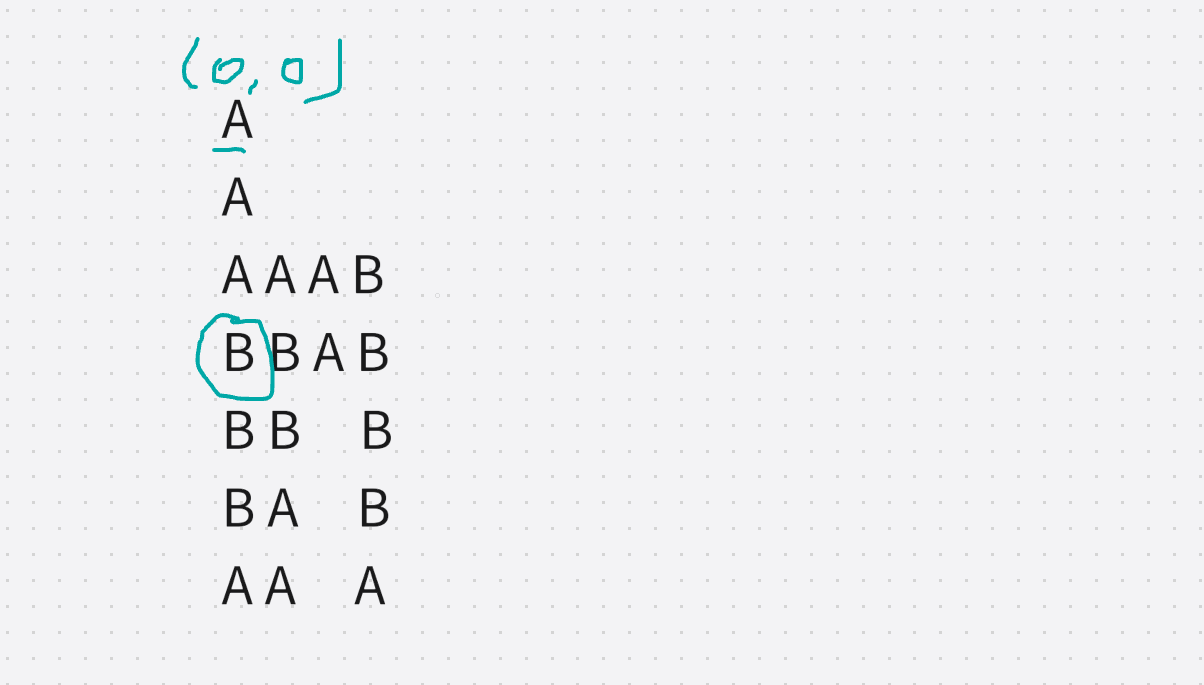
如下图:
图中圈起来的B, 当每一步走的是: 下下下下, 此时第一次遍历到B, st[3][0][0] = true, 然后继续 下下下右上上上左, 此时又一次遍历到这个B, st[3][0][2] = true, 最后上右右右下下下下, 到达(n,m)
- 当第一次遍历到B的时候st中的z = 0, 因为此时的B位于BBB的第一个
- 当第二次遍历到B的时候st中的z = 2, 因为此时的B位于BBB的第三个
如果我们用的还是二维st, 那么就不可能第二次遍历到B, 也就找不到答案了
ac代码👇
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int x, y, deep, step; // deep深度, step是一共走的步数, 初始位置也算一步, deep初始化是0, step初始化是1
};
const int N = 1e3 + 10;
int n, m, k;
char g[N][N];
bool st[N][N][20]; // 打标记, 看之前是否走过, 防止进入死循环
int go[N][N] = {{0, 1}, {0, - 1}, {1, 0}, {-1, 0}}; // 四个方向可以走
int bfs()
{
queue<Node> q;
q.push({0, 0, 0, 1}); st[0][0][0] = true;
while (q.size())
{
auto t = q.front();
q.pop();
if (t.x == n - 1 && t.y == m - 1) return t.deep; // 找到答案, 返回
for (int i = 0; i < 4; i ++)
{
int aa = t.x + go[i][0], bb = t.y + go[i][1], stp = t.step + 1;
if (aa < 0 || aa >= n || bb < 0 || bb >= m) continue; // 超出边界, 跳过循环
if (stp > k) // 需要转换字符
{
stp = 1;
if (g[aa][bb] == g[t.x][t.y]) continue; // 如果字符跟原来相同, 跳过
}
else // 不需要转换字符
{
if (g[aa][bb] != g[t.x][t.y]) continue; // 如果字符跟原来不同, 跳过
}
if (!st[aa][bb][stp]) // 没有访问过
{
st[aa][bb][stp] = true;
q.push({aa, bb, t.deep + 1, stp});
}
}
}
return -1; // 没有找到答案, 无解
}
int main()
{
cin >> n >> m >> k;
for (int i = 0; i < n; i ++) cin >> g[i];
int res = bfs();
cout << res << endl;
return 0;
}
觉得写的不错的话, 点个赞吧~
