leetcode(力扣) 2866. 美丽塔 II
给定一个长度为 n 的整数数组 maxHeights,下标从 0 开始。
任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i,高度为 heights[i]。
如果满足以下条件,则称这些塔是美丽的:
- 1 ≤ heights[i] ≤ maxHeights[i]
- heights 是一个山脉数组,即存在一个下标 i 满足:
- 对于所有 0 < j ≤ i,heights[j - 1] ≤ heights[j]
- 对于所有 i ≤ k < n - 1,heights[k + 1] ≤ heights[k]
请返回满足美丽塔要求的方案中,高度和的最大值。
示例 1:
输入:maxHeights = [5, 3, 4, 1, 1]
输出:13
解释:高度和最大的美丽塔方案为 heights = [5, 3, 3, 1, 1],这是一个美丽塔方案,因为:
- 1 ≤ heights[i] ≤ maxHeights[i]
- heights 是一个山脉数组,峰值在 i = 0 处。
示例 2:
输入:maxHeights = [6, 5, 3, 9, 2, 7]
输出:22
解释:高度和最大的美丽塔方案为 heights = [3, 3, 3, 9, 2, 2],这是一个美丽塔方案,因为:
- 1 ≤ heights[i] ≤ maxHeights[i]
- heights 是一个山脉数组,峰值在 i = 3 处。
示例 3:
输入:maxHeights = [3, 2, 5, 5, 2, 3]
输出:18
解释:高度和最大的美丽塔方案为 heights = [2, 2, 5, 5, 2, 2],这是一个美丽塔方案,因为:
- 1 ≤ heights[i] ≤ maxHeights[i]
- heights 是一个山脉数组,峰值在 i = 2 处。
注意,在这个方案中,i = 3 也是一个峰值。
提示:
- 1 ≤ n = maxHeights.length ≤ 10^5
- 1 ≤ maxHeights[i] ≤ 10^9
题解:
暴力做法 (时间复杂度 O(n^2))
每次选取下标 i 为峰值, 进行 n 次,对每次取max就可以找到答案
-
对于 i 左边的序列: 需要满足序列是非递减的, 同时每个值尽可能大
- 所以满足: j 的位置上的数 <= (j, i] 上的最小的值 (等于时取得最大值) , 同时需要保证 j 位置上的数要小于heights[j] (题目中的要求,美丽塔的要求); 即 t = min(pre, heights[j]) pre表示的是 下标是 (j, i] 的最小的值
-
对于 i 右边的序列: 需要满足序列是非递增的,同时每个值尽可能大
- 所以满足:j 的位置上的数 <= [i, j) 上的最小的值 (等于时取得最大值), 同时需要保证 j 位置上的数要小于heights[j]; 即 t = min(pre, heights[j]) pre表示的是 下标是 [i, j) 的最小的值
ac代码👇(美丽塔 I 可ac, II不行, 时间复杂度太高)
class Solution {
public:
long long maximumSumOfHeights(vector<int>& heights) {
int n = heights.size();
long long res = 0;
for (int i = 0; i < n; i ++ )
{
int pre = heights[i];
long long sum = heights[i] * 1LL;
for (int j = i - 1; j >= 0; j --) // pre表示的是下标 (j, i] 中heights中的最小值
{
sum += min(pre, heights[j]); // 下标从i - 1开始, 每次取min,可以保证当下标为 j 时 pre 表示的就是 [j + 1, i] 的最小值
pre = min(pre, heights[j]);
}
pre = heights[i];
for (int j = i + 1; j < n; j ++) // pre表示的是下标 [i, j) 中heights中的最小值
{
sum += min(pre, heights[j]);
pre = min(pre, heights[j]);
}
res = max(sum, res);
}
return res;
}
};
单调栈做法 (时间复杂度 O(n)) (tag: 单调栈、 动态规划)
st1 和 st2 存的都是下标
下面图片模拟的是 第一个 for循环, 标红的是 进入 if(st1.empty()) 这个分支的
p1[4] 为什么加的是 2 x heights[4]呢, 因为此时st1中还有 元素1的下标2, 此时 下标3 和 下标4 的高度应该都为heights[4]
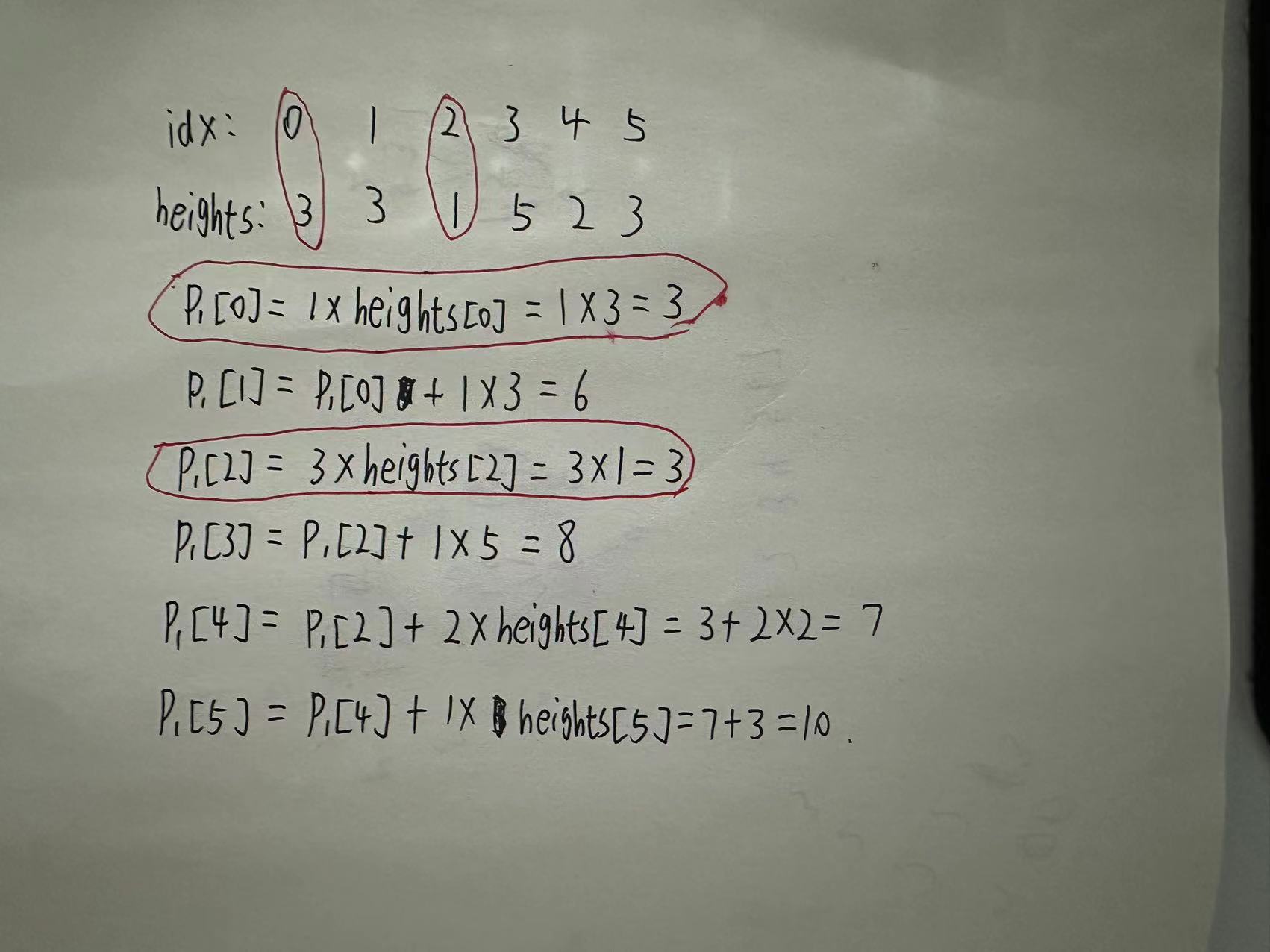
ac代码👇
class Solution {
public:
long long maximumSumOfHeights(vector<int>& heights) {
int n = heights.size();
long long res = 0;
stack<int> st1; stack<int> st2; // 栈里面存的是 下标
vector<long long> p1(n); vector<long long> p2(n);
// p1 的状态表示是 下标为 i 的 左侧美丽塔高度之和 (包含i本身,同时满足p1[i]是美丽塔高度和的最大值)
// p2 的状态表示是 下标为 i 的 右侧美丽塔高度之和 (包含i本身,同时满足p1[i]是美丽塔高度和的最大值)
for (int i = 0; i < n; i ++)
{
while (!st1.empty() && heights[i] < heights[st1.top()]) st1.pop(); // 让栈满足 (栈为空 || 栈中元素对应的heights的值是非递减的)
// 栈为空 说明 : i = 0或者 i 前面的山脉高度都比 heights[i] 大, 为了保证序列非递减, 前面的所有数都应该是 heights[i]
if (st1.empty()) p1[i] = (long long)(i + 1) * heights[i];
else p1[i] = p1[st1.top()] + (long long)(i - st1.top()) * heights[i] ;
// 不为空 说明 下标为 (st1.top(), i] 山脉高度 都比 heights[i] 大, 为了保证序列非递减, (st1.top(), i] 之间的山脉高度都应该是 heights[i]
st1.emplace(i);
}
for (int i = n - 1; i >= 0; i --) // 需要保证从后往前是一个非递减序列
{
while (!st2.empty() && heights[i] < heights[st2.top()]) st2.pop();
if (st2.empty()) p2[i] = (long long)(n - i) * heights[i] * 1LL;
else p2[i] = p2[st2.top()] + (long long)(st2.top() - i) * heights[i] ;
st2.emplace(i);
res = max(res, p1[i] + p2[i] - heights[i]); // 看p1和p2的状态表示,都包含的 i,要减去重复的一个
}
return res;
}
};
觉得写的不错的话,点个赞吧!~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号