Dijkstra迪杰斯特拉求最短路和最短路的条数和各个点权值的最大值

作为一个城市的紧急救援队队长，你会得到一张你所在国家的特殊地图。 该地图显示了由一些道路连接的几个分散的城市。
地图上标出了每个城市的救援队伍数量以及任意两个城市之间每条道路的长度。 当其他城市接到紧急电话时，你的工作就是尽快带领你的人员赶到现场，同时在途中召集尽可能多的人手。

输入规格：

每个输入文件包含一个测试用例。 对于每个测试用例，第一行包含 4 个正整数：N (≤500) - 城市数量（城市编号从 0 到 N−1），M - 道路数量，C 1 和 C 2 - 分别是您当前所在的城市和必须救援的城市。 下一行包含N个整数，其中第i个整数是第i个城市的救援队数量。 接下来是M行，每行描述一条具有三个整数c 1 、c 2 和L的道路，这三个整数分别是由一条道路连接的一对城市和该道路的长度。 保证从C 1 到C 2 至少存在一条路径。

输出规格：

对于每个测试用例，在一行中打印两个数字：C 1 和 C 2 之间不同的最短路径的数量，以及您可能聚集的救援队的最大数量。 一行中的所有数字必须恰好由一个空格分隔，并且行尾不允许有多余的空格。

输入示例：

5 6 0 2
1 2 1 5 3
0 1 1
0 2 2
0 3 1
1 2 1
2 4 1
3 4 1

示例输出：

2 4

题解:

迪杰斯特拉主要思想就是： 每次选取距离源点最近的 不在源点这个集合 的点，并把该点加入源点这个集合，然后更新一下其他点到源点的最短距离，进行 n - 1次就行了

这里讲一下 cnt 和 num 数组
cnt 数组存储的是 从源点到达 点i的最短距离的总个数
num 数组存储的是 从源点到达 点i的最短距离前提下 所能聚集的救援队数量的最大值

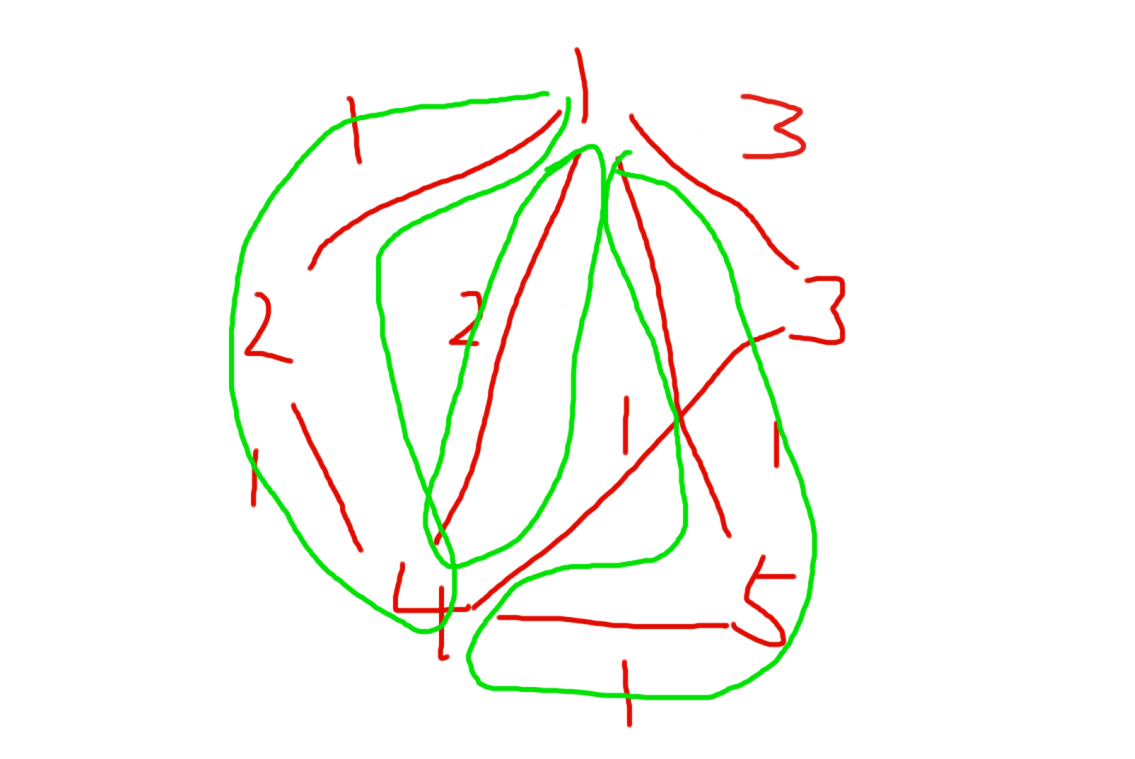
解释一下为什么dist[t] + g[t][j] == dist[j]时, cnt[j] += cnt[t]; 如下图 假设源点是1，cnt[4] = 3，即有3条达到4的最短路，那么cnt[3] = cnt[3] + cnt[4] = 4

    #include <bits/stdc++.h>
    using namespace std;
    const int N = 510;
    int g[N][N], dist[N], Peonum[N];
    int cnt[N], num[N];     // 最短路的条数 和 最短路前提下最多能拉多少救援人员
    bool st[N];             // 标记，选过的点不再选
    int n, m, start, save;

    void djs()
    {
        memset(dist, 0x3f, sizeof dist); 

        // 初始化
        dist[start] = 0;
        cnt[start] = 1;     
        num[start] = Peonum[start];

        for (int i = 0; i < n; i ++)
        {
            int t = -1;
            for (int j = 0; j < n; j ++)
                if (!st[j] && (t == -1 || dist[j] < dist[t]))
                    t = j;
            st[t] = true;
            for (int j = 0; j < n; j ++)
            {
                if (dist[t] + g[t][j] < dist[j])
                {
                    dist[j] = dist[t] + g[t][j];
                    cnt[j] = cnt[t];
                    num[j] = num[t] + Peonum[j];
                }
                else if (dist[t] + g[t][j] == dist[j])
                {
                    cnt[j] += cnt[t];
                    num[j] = max(num[j], num[t] + Peonum[j]);
                }
            }
        }
    }
    int main()
    {
        cin >> n >> m >> start >> save;
        memset(g, 0x3f, sizeof g);          // 初始化，最开始没有点是相连的 (0x3f是个很大的值)
        for (int i = 0; i < n; i ++) cin >> Peonum[i];
        for (int i = 0; i < m; i ++)
        {
            int a, b, c; cin >> a >> b >> c;
            g[a][b] = g[b][a] = min(g[a][b], c);
        }
        djs();
        cout << cnt[save] << ' ' << num[save] << endl;
        return 0;
    }

觉得写的不错的话，点个赞吧~