已知二叉树的后序和中序遍历求前序遍历
假设二叉树上各结点的权值互不相同且都为正整数。
给定二叉树的后序遍历和中序遍历,请你输出二叉树的前序遍历序列。
输入格式:
第一行包含整数 N,表示二叉树结点总数。
第二行给出二叉树的后序遍历序列。
第三行给出二叉树的中序遍历序列。
输出格式
输出二叉树的前序遍历
数据范围
1≤N≤50000,
二叉树结点权值范围 [1,1e9]。
样例输入:
7
1 2 3 4 5 6 7
2 1 4 3 7 5 6
样例输出:
7 4 2 1 3 6 5
题解:
已知,树的后序遍历最后一个数就是该树(子树)的 root 节点,我们每次只需要取后序遍历的最后一个节点就行~~
代码当中的build函数传递的分别是 一棵树(子树)后序遍历的左右闭区间 和 中序遍历的左右闭区间
这题比较难确定的是build函数中的第二个参数,也就是后序遍历的右区间
这里我们令其为 x ,下面我给出一个图来表示 x 的计算过程
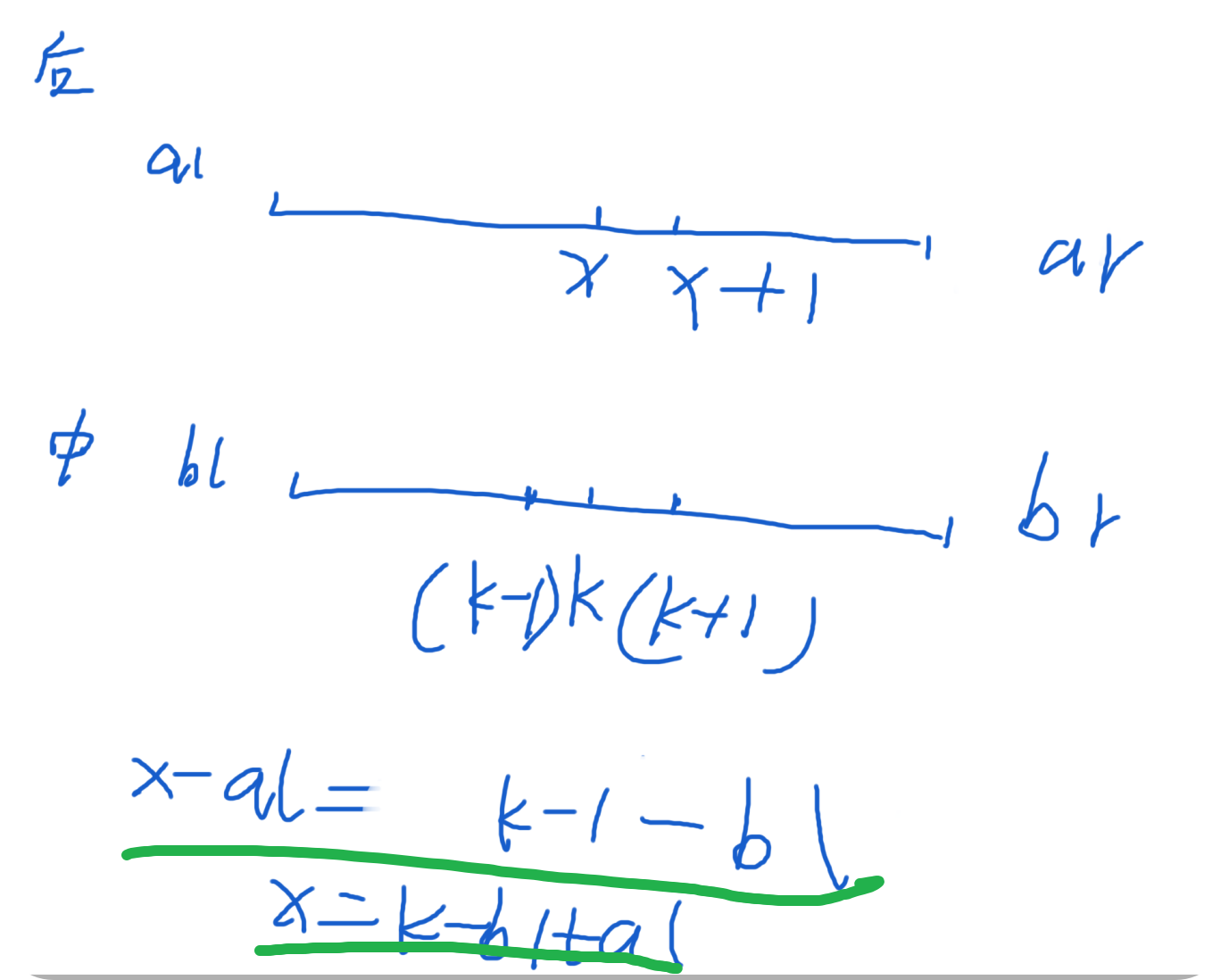
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
unordered_map<int,int> l, r, c;
int build(int al, int ar, int bl, int br) // a 是后序, b 是中序
{
int root = a[ar]; // 后序遍历的最后一个数 是该树的根节点, 子树也是
int k = c[root]; // 👇 这个是 x
if (k > bl) l[root] = build(al, k - bl + al - 1, bl, k - 1);
if (k < br) r[root] = build(k - bl + al, ar - 1, k + 1, br);
// 👆这个是 x + 1
return root;
}
int n;
void print(int root)
{
cout << root << endl;
if (l[root] != 0) print(l[root]);
if (r[root] != 0) print(r[root]);
}
int main()
{
cin >> n;
for (int i = 0; i < n; i ++) cin >> a[i];
for (int i = 0; i < n; i ++)
{
cin >> b[i]; c[b[i]] = i;
// c 用来存储 节点 x, 即b[i] 在中序遍历中的下标
}
int root = build(0, n -1, 0, n - 1);
print(root);
return 0;
}
觉得写的不错的话,点个赞吧


 浙公网安备 33010602011771号
浙公网安备 33010602011771号