普里姆算法（Prim算法）(最小生成树算法)-贪心

普里姆算法（Prim算法）：图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点（英语：Vertex (graph theory)），且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（英语：Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（英语：Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

发现一个好的讲解视频：https://www.bilibili.com/video/BV1Eb41177d1?from=search&seid=2272848912623613091

发现了一个我看懂的文章：https://blog.csdn.net/yeruby/article/details/38615045?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522159088128019195264560599%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=159088128019195264560599&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~baidu_landing_v2~default-3-38615045.first_rank_ecpm_v1_pc_rank_v3&utm_term=prim

 

lowcost[i]:  表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST

mst[i]:  表示对应lowcost[i]的起点

 

以V1为起始点，将各点与V1的联系存入lowcost数组中，mst数组都默认为V1起点

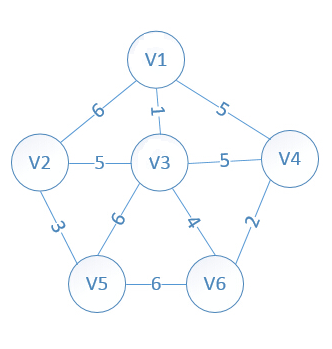
遍历lowcost数组，找最小值(min)，将最小值(min)存入sum中，并将lowcost[最小值下标(minid)]赋值为0（表示此点已被选）

之前的lowcost数组存储的是各点与V1的联系，再次遍历lowcost数组，判断各点与新加进来的点（V3）的联系是否小于之前的，小于就覆盖

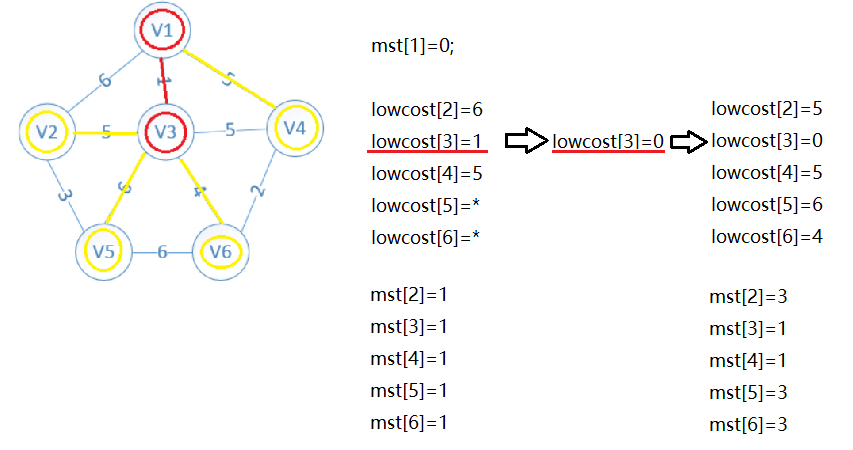
遍历lowcost数组，找最小值(min)，将最小值(min)存入sum中，并将lowcost[最小值下标(minid)]赋值为0（表示此点已被选）

之前的lowcost数组存储的是各点与V1 V3的联系，再次遍历lowcost数组，判断各点与新加进来的点（V6）的联系是否小于之前的，小于就覆盖

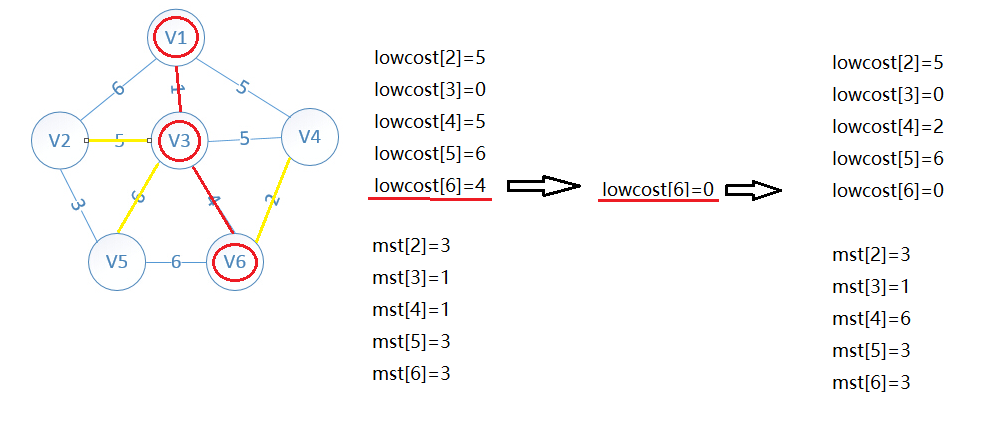
下面的都是这样，以此类推...

输入：

6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6

输出：

V1-V3=1
V3-V6=4
V6-V4=2
V3-V2=5
V2-V5=3
15

 代码：

#include <iostream>
#include <bits/stdc++.h>
using namespace std;

#define MAX 100  
#define MAXCOST 0x7fffffff  //int型最大值

void prim(int graph[][MAX],int n)
{
    int lowcost[MAX];
    int mst[MAX];
    int sum=0;
    for(int i=2;i<=n;i++)//以V1为起始点，遍历lowcost数组 
    {
        lowcost[i]=graph[1][i];
        mst[i]=1;
    }
    mst[1]=0;
    for(int i=2;i<=n;i++)//计算n-1个点
    {
        int min=MAXCOST;
        int minid=0;
        for(int j=2;j<=n;j++)//遍历lowcost数组，找最小值
        {
            if(lowcost[j]<min && lowcost[j]!=0)
            {
                min=lowcost[j];//最小值
                minid=j;//最小值下标
            }
        }
        cout<<"V"<<mst[minid]<<"-V"<<minid<<"="<<min<<endl;
        sum+=min;
        lowcost[minid]=0;
        for(int j=2;j<=n;j++)
        {
            if(graph[minid][j]<lowcost[j])
            {
                lowcost[j]=graph[minid][j];
                mst[j]=minid;
            }
        }
    }
    cout<<sum;
}
int main()
{
    int n,m;
    int graph[MAX][MAX];
    cin>>n>>m;
    //初始化图G
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            graph[i][j]=MAXCOST;
        }
    }
    //构建图G
    for(int k=1;k<=m;k++)
    {
        int i,j,cost;
        cin>>i>>j>>cost;
        graph[i][j]=cost;
        graph[j][i]=cost;
    }
    prim(graph,n);
    return 0;
}