假币问题-减治法

减治法定义：将问题分成若干子问题，只解决其中的一个适合的子问题。

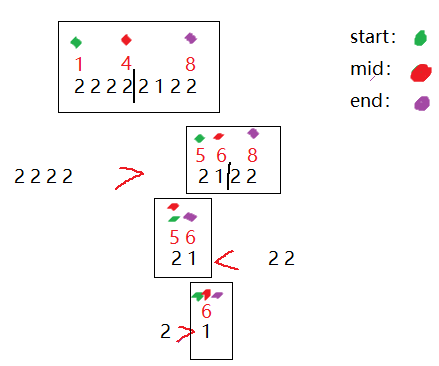
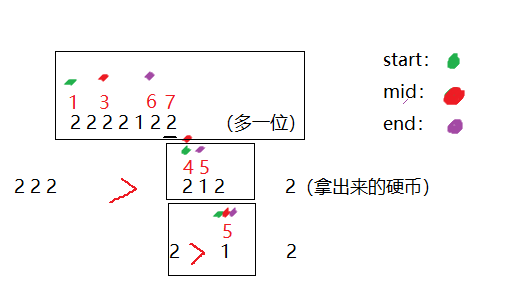
问题描述：n个硬币中有一个假币，假的硬币比真的硬币轻，一个只有0刻度的天平，求出假币的位置。

 

输入：

8

2 2 2 2 2 1 2 2

输出：

6

当n为偶数（start+end）为奇数时，将n个硬币等分，比较谁轻，轻的一方有假币。以此类推。

当n为奇数（start+end）为偶数时，多一个硬币，将它拿出来，剩下的按n为偶数处理，如果两方重量相等那么拿出来的硬币为假币。

看图可知如果两方比较相等，多出来的（最后的硬币）就是假币或者当start==end时当前硬币就是假币。

        

代码： 

#include<iostream>

using namespace std;

void false_money(int a[],int start,int end)
{

    if(start==end)
    {
        cout<<start;
        return;
    }
    if((start+end)%2==0)//多一个硬币，最后一个硬币拿出来
    {
        end--;
    }
    int sum1=0,sum2=0;
    int mid=(start+end)/2;
    for(int i=start;i<=mid;i++)
    {
        sum1+=a[i];
    }
    for(int i=mid+1;i<=end;i++)
    {
        sum2+=a[i];
    }

    if(sum1==sum2)//当两方硬币重量相等，多出来的硬币就是假币
    {
        cout<<end+1;
        return;
    }
    else if(sum1<sum2)
    {
        false_money(a,start,mid);
    }
    else
    {
        false_money(a,mid+1,end);
    }
}
int main()
{
    int n;
    int a[100];
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    false_money(a,1,n);
    return 0;
}