最大子段和-3种方法

问题描诉： 给定有n个整数(可能为负整数)组成的序列a1,a2,...,an,求该序列连续的子段和的最大值和区间。 如果该子段的所有元素和是负整数时定义其最大子段和为0。

输入：1 -2 4 5 -2 8 3 -2 6 3 7 -1

输出：32 , [3 , 11]

 

蛮力法：

时间：O(n³)

#include<iostream>

using namespace std;

int main()
{
    int a[20];
    int n;
    int max=0;
    int x,y;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    for(int i=1;i<=n;i++)  //左区间
    {
        for(int j=i;j<=n;j++)  //右区间
        {
            int sum=0;
            for(int k=i;k<=j;k++)  //区间内的和
            {
                sum+=a[k];
            }
            if(sum>max)
            {
                max=sum;
                x=i,y=j;
            }
        }
    }
    if(max>0)
    {
        cout<<max<<" , ["<<x<<" , "<<y<<"]";
    }
    else
    {
        cout<<0;
    }
    return 0;
}

分治法：

时间：O(n*logn)

最大子段和的区间有三种情况：

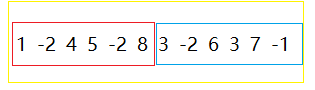
左半部分、右半部分和跨越中间部分

 

递归：

s1=左面最大子段和  s2=右面最大子段和  s3=s1+s2+他们中间的数

 

                                                  

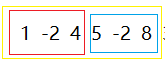
                                               s1=4  s2=11  s3=15，最大子段和为15，区间【4,8】

                                                                               

s1=1  s2=4  s3=3，最大子段和为4，区间【4】                    s1=5  s2=8  s3=11，最大子段和为11，区间【5,8】

                                                                                     

s1=-2  s2=4  s3=2，最大子段和为4，区间【4】                  s1=-2  s2=8  s3=6，最大子段和为8，区间【8】

#include<iostream>
using namespace std;

int MaxSubArray(int a[],int left,int right)
{
    int mid=(left+right)/2;
    int s1,s2,sum=0;
    int max=-10000;  //max相当于s3
    if(left==right)
    {
        return a[left];
    }
    s1=MaxSubArray(a,left,mid);  //左递归
    s2=MaxSubArray(a,mid+1,right);  //右递归
    for(int i=mid;i>=0;i--)   //从左半部分最后一个数向前加找出最大值
    {
        sum+=a[i];
        if(max<sum)
        {
            max=sum;
        }
    }
    sum=max;  //保留最大值
    for(int i=mid+1;i<=right;i++)    //从右半部分第一个数向后加找出最大值
    {
        sum+=a[i];
        if(max<sum)
        {
            max=sum;
        }
    }
    if(max<s1)
    {
        max=s1;
    }
    else if(max<s2)
    {
        max=s2;
    }return max;
}
int main()
{
    int a[20];
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
    }
    cout<<MaxSubArray(a,0,n-1);
    return 0;
}

 动态规划法：

时间：O(n)

输入12个整数存入a[n]中， D[n]中存后  i  项子段和，Rec[n]存结尾数组。最后一个元素先初始化。

例如

i=11，D[11]=-1; Rec[11]=12;       初始化

i=10，D[10]=7;Rec[10]=11;        //如果D[i+1]<0 跳过

i=9，D[9]=D[10]+a[9]=10; Rec[10]=11;       //下标为9的元素后的和

i=8，D[8]=D[9]+a[8]=16;Rec[10]=11;   

i=7，D[7]=;D[8]+a[7]=14;  ...(都是Rec[]=11)

i=6，D[6]=D[7]+a[6]=17;   ...  

i=5，D[5]=D[6]+a[5]=25;   ...   

i=4，D[4]=D[5]+a[4]=23;   ...

i=3，D[3]=;D[4]+a[3]=28;  ...

i=2，D[2]=D[3]+a[2]=32;  ...

i=1，D[1]=D[2]+a[1]=30;  ...  

i=0，D[0]=D[1]+a[0]=31; ...

 找出最大值32，区间为[3，11]   //第3个数到第11个数

#include<iostream>

using namespace std;

void MaxSubArray(int a[],int D[],int Rec[],int n)
{
    int max=n;
    for(int i=n-1;i>=0;i--)  //从倒数第二个元素开始
    {
        if(D[i+1]>0)
        {
            D[i]=D[i+1]+a[i];
            Rec[i]=Rec[i+1];
        }
        else
        {
            D[i]=a[i];
            Rec[i]=i+1;
        }
        if(D[i]>D[max])
        {
            max=i;
        }
    }
    cout<<D[max]<<" , ["<<max+1<<" , "<<Rec[max]<<"]";
}
int main()
{
    int a[20];
    int D[20];
    int Rec[20];
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>a[i];

    }
    Rec[n-1]=n;D[n-1]=a[n-1];
    MaxSubArray(a,D,Rec,n-1);
    return 0;
}