haber 计算几何专题
A - Windy Path
感觉不简单啊,大家怎么都会/jk
假设当前已经找了一个满足一段前缀的方案,对剩下的点求凸包,不难发现我们可以找到一个点,满足从当前点到这个点再到其他点一定是向左/向右,直接暴力枚举即可 \(\mathcal{O}(n^3)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define id(x,y) ((x-1)*n+y)
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=2e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
int x,y;
Point(const int &_x=0,const int &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const int &k){return Point(x*k,y*k);}
};
int dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
int det(Point a,Point b){return a.x*b.y-a.y*b.x;}
int Dist(Point a,Point b){return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);}
Point p[55];int n,st,vis[55];char s[55];
int sol(int u,int t){
for(int v=1;v<=n;v++){
int flag=1;if(v==u||vis[v])continue;
for(int i=1;i<=n;i++){
if(i==u||i==v||vis[i])continue;
if(s[t]=='L'&&det(p[v]-p[u],p[i]-p[v])<0)flag=0;
if(s[t]=='R'&&det(p[v]-p[u],p[i]-p[v])>0)flag=0;
if(!flag)break;
}
if(flag)return v;
}
return 0;
}
signed main(){
n=read(),st=1;
for(int i=1;i<=n;i++)p[i].x=read(),p[i].y=read();
scanf("%s",s+1);
for(int i=1;i<=n;i++)if(p[i].x<p[st].x)st=i;
for(int i=1;i<=n-2;i++)printf("%lld ",st),vis[st]=1,st=sol(st,i);
printf("%lld ",st);vis[st]=1;
for(int i=1;i<=n;i++)if(!vis[i])printf("%lld ",i);
return 0;
}
B - Spin Doctor
C - United States of Eurasia
二分答案,最远点对即求凸包后跑旋转卡壳,考虑从起点开始二分每一段的终点。注意到这样做单次 check 复杂度 \(\mathcal{O}(len)\),在最后答案段长很短时很浪费,考虑沿用小黄鸭那个题的做法,倍增找一个合适的区间,然后再二分,总复杂度 \(\mathcal{O}(n\log n\log V)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=2e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
inline void print(int x){
if(x>9)print(x/10);
putchar(x%10+'0');
}
struct Point{
int x,y;
Point(const int &_x=0,const int &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const int &k){return Point(x*k,y*k);}
};
int dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
int det(Point a,Point b){return a.x*b.y-a.y*b.x;}
int Len(Point a){return sqrtl(dot(a,a));}
int Dist(Point a,Point b){return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);}
struct Line{
Point x,y;
Line(const Point &_x,const Point &_y):x(_x),y(_y){}
};
//int DistLine(Line a,Point b){
// return fabs(det(a.x,b-a.y))/Len(a.x);
//}
int n,k,st[250005],used[250005];Point p[250005];
vector<Point>ConvexHull(vector<Point>P){
int top=0,len=(int)P.size();vector<Point>convex;
st[++top]=0;
for(int i=1;i<len;i++){
while(top>=2&&det(P[st[top]]-P[st[top-1]],P[i]-P[st[top]])<=0)top--;
st[++top]=i;
}
for(int i=1;i<=top;i++)if(!used[st[i]])convex.push_back(P[st[i]]),used[st[i]]=1;
top=0;st[++top]=len-1;
for(int i=len-2;i>=0;i--){
while(top>=2&&det(P[st[top]]-P[st[top-1]],P[i]-P[st[top]])<=0)top--;
st[++top]=i;
}
for(int i=1;i<=top;i++)if(!used[st[i]])convex.push_back(P[st[i]]),used[st[i]]=1;
for(int i=0;i<len;i++)used[i]=0;
return convex;
}
int myabs(int x){
return ((x<0)?-x:x);
}
int RotatingCalipers(vector<Point>P){
int len=(int)P.size();
if(len<=1)return 0;
if(len==2)return Dist(P[0],P[1]);
if(len==3)return max({Dist(P[0],P[1]),Dist(P[1],P[2]),Dist(P[0],P[2])});
int res=0;
for(int i=0,j=0;i<len;i++){
while(myabs(det(P[(i+1)%len]-P[i],P[j]-P[(i+1)%len]))<=myabs(det(P[(i+1)%len]-P[i],P[(j+1)%len]-P[(i+1)%len])))j=(j+1)%len;
res=max(res,max(Dist(P[i],P[j]),Dist(P[(i+1)%len],P[j])));
}
return res;
}
int sol(int l,int r){
vector<Point>P;
for(int i=l;i<=r;i++)P.push_back(p[i]);
return RotatingCalipers(ConvexHull(P));
}
int check(int m){
int pos=1,cnt=0;
while(pos<=n){
int t=1,flag=1;
while(flag){
if(sol(pos,min(n,pos+t-1))>m)break;
else if(pos+t-1>n){flag=0;break;}
t=t+t;
}
if(!flag){cnt++;break;}
int l=pos+t/2,r=min(n,pos+t-1),res=pos+t/2-1;
while(l<=r){
int mid=(l+r)>>1;
if(sol(pos,mid)<=m)res=mid,l=mid+1;
else r=mid-1;
}
while(res>=pos&&res+1<=n&&p[res].x==p[res+1].x)res--;
if(res<pos)return 0;
cnt++,pos=res+1;
}
return (cnt<=k);
}
signed main(){
n=read(),k=read();
for(int i=1;i<=n;i++)p[i].x=read(),p[i].y=read();
sort(p+1,p+n+1,[](Point x,Point y){
return tie(x.x,x.y)<tie(y.x,y.y);
});
int l=0,r=inf,res=r;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid))res=mid,r=mid-1;
else l=mid+1;
}
print(res);
return 0;
}
D - Jungle Outpost
注意到我们只会删去一段连续的点,考虑二分答案,问题即求半平面交的面积是否为 0,复杂度 \(\mathcal{O}(n\log^2 n)\),瓶颈在于需要排序。
点击查看代码
#include<bits/stdc++.h>
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const double eps=1e-7;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
double x,y;
Point(const double &_x=0,const double &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const double &k){return Point(x*k,y*k);}
};
double dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
double det(Point a,Point b){return a.x*b.y-a.y*b.x;}
struct Line{
Point p,way;double ang;
Line(const Point &_p=Point(0,0),const Point &_way=Point(0,0)):p(_p),way(_way){}
};
int OnRight(Line x,Point y){return det(x.way,y-x.p)<=-eps;}
Point Intersect(Line x,Line y){return x.p+x.way*(det(y.way,x.p-y.p)/det(x.way,y.way));}
Line q[100005];Point p[100005];
vector<Point>HalfPlane(vector<Line>poly){
int len=(int)poly.size();
for(int i=0;i<len;i++)poly[i].ang=atan2(poly[i].way.y,poly[i].way.x);
sort(poly.begin(),poly.end(),[](Line x,Line y){
return x.ang<y.ang;
});
int L=1,R=0;q[++R]=poly[0];vector<Point>convex;
for(int i=1;i<len;i++){
while(L<R&&OnRight(poly[i],p[R]))R--;
while(L<R&&OnRight(poly[i],p[L+1]))L++;
q[++R]=poly[i];
if(L<R&&fabs(det(q[R].way,q[R-1].way))<=eps){
if(OnRight(q[R],q[R-1].p)&&dot(q[R].way,q[R-1].way)<=-eps)return convex;
R--;
if(!OnRight(q[R],poly[i].p))q[R]=poly[i];
}
if(L<R)p[R]=Intersect(q[R],q[R-1]);
}
while(L<R&&OnRight(q[L],p[R]))R--;
if(R-L<=1)return convex;
p[L]=Intersect(q[L],q[R]);
for(int i=L;i<=R;i++)convex.push_back(p[i]);
return convex;
}
double GetArea(vector<Point>poly){
int len=(int)poly.size();
if(len<=2)return 0;
double res=0;
for(int i=0;i<len;i++)res+=det(poly[i],poly[(i+1)%len]);
return res/2;
}
int n;Point P[50005];
int check(int mid){
vector<Line>line;
for(int i=0;i<n;i++){
line.push_back(Line(P[i],P[i]-P[(i+1+mid)%n]));
line.push_back(Line(P[i],P[i]-P[(i+1)%n]));
}
return ((GetArea(HalfPlane(line)))<eps);
}
signed main(){
freopen("jungle.in","r",stdin);
freopen("jungle.out","w",stdout);
n=read();
for(int i=0;i<n;i++)P[i].x=read(),P[i].y=read();
int l=1,r=n-1,res=n;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid))res=mid,r=mid-1;
else l=mid+1;
}
printf("%d\n",res);
return 0;
}
E - Security at Museums
佳老师讲的,感觉有一步非常有思维含金量啊。
考虑什么时候任意一对点都能互相看到。显然凹多边形是不行的,因为凹进去的部分的两边的点无法互相看到。然后这个凸多边形必须在给定的博物馆范围内,不能和边界交。现在问题即求有多少个在给定范围内的凸多边形。
考虑在这个凸多边形的最左最上统计一个它。定义 \(f_{i,j}\) 表示凸包上最后两个点依次为 \(i,j\) 的凸包数量,转移时满足斜率不增即可,因为可以三点共线,并不是严格凸包。复杂度 \(\mathcal{O}(n^4)\),不太能跑。
思考为什么我们 dp 状态要记录两维?因为我们要保证转移时斜率不增。有一个聪明的思考是我们可以事先把所有转移预处理出来,按斜率排好序,这样就可以直接按顺序转移了,就只需要记录一维状态了捏,复杂度 \(\mathcal{O}(n^3)\)。注意这样做在多点共线时会算重,需要特判。
F - Gravitational Wave Detector
G - Dividing Area
注意到加边可以时间倒流成删边,考虑并查集维护。思考如何求一条边逆时针方向的面积。注意题目保证了不会有在非端点处相交的边,且会加边到不能加为止。所以一些特殊情况比如一环套一环这种是不会出现的。
假设当前逆时针方向是一个多边形,直接用叉积算面积即可,此时每条边贡献可以拆开,容易维护。注意到沿用此方法时如果逆时针方向是无限大的平面时,算出来的“面积”是 \(\le 0\) 的!比如一个这样的图形
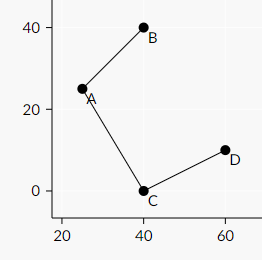
原来是 \(B\to A\to C\to D\) 的四边形,删去 \(D\to B\) 后每条边的贡献被反边一一抵消,贡献为 0。再比如一个 C 字上附着若干个多边形,C 字部分的贡献相互抵消结果为 0,此时减去多边形的面积后总贡献为负数。不懂可以画图理解一下。复杂度 \(\mathcal{O}(n\log n)\),瓶颈在于极角排序。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define fi first
#define se second
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
int x,y;
Point(const int &_x=0,const int &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const int &k){return Point(x*k,y*k);}
inline int pos(){
if(y>0)return 1;
else if(y==0&&x>=0)return 0;
else return -1;
}
};
int dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
int det(Point a,Point b){return a.x*b.y-a.y*b.x;}
int fa[2000005],siz[2000005];Point p[200005];vector<int>g[200005];map<int,int>mp[200005];
int find(int x){
return ((x==fa[x])?x:fa[x]=find(fa[x]));
}
void merge(int x,int y){
if((x=find(x))==(y=find(y)))return;
fa[y]=x,siz[x]+=siz[y];
}
int op[1000005],a[1000005],b[1000005],ans[1000005];
signed main(){
int n=read();
for(int i=1;i<=n;i++)p[i].x=read(),p[i].y=read();
int m=read();
for(int i=1;i<=m;i++){
op[i]=read(),a[i]=read()+1,b[i]=read()+1;
if(op[i]==1){
g[a[i]].push_back(b[i]),g[b[i]].push_back(a[i]);
mp[a[i]][b[i]]=i,mp[b[i]][a[i]]=i+m;fa[i]=i,fa[i+m]=i+m;
siz[i]=det(p[a[i]],p[b[i]]),siz[i+m]=det(p[b[i]],p[a[i]]);
}
}
for(int i=1;i<=n;i++){
sort(g[i].begin(),g[i].end(),[&](int x,int y){
if((p[x]-p[i]).pos()!=(p[y]-p[i]).pos())return (p[x]-p[i]).pos()<(p[y]-p[i]).pos();
return det(p[x]-p[i],p[y]-p[i])>0;
});
int len=(int)g[i].size();if(!len)continue;
for(int o=0;o<len;o++){
int j=g[i][o],k=g[i][(o+1)%len];
merge(mp[i][j],mp[k][i]);
}
}
for(int i=m;i>=1;i--){
if(op[i]==1)merge(mp[a[i]][b[i]],mp[b[i]][a[i]]);
else ans[i]=siz[find(mp[a[i]][b[i]])];
}
for(int i=1;i<=m;i++)if(op[i]==0)printf("%lld\n",((ans[i]<=0)?-1ll:ans[i]));
return 0;
}
H - Kingdom Partition
维护前缀凸包和后缀凸包即可。复杂度 \(\mathcal{O}(n\log n)\),瓶颈在排序。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=2e18,N=1e4;
const double eps=1e-6;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
int x,y;
Point(const int &_x=0,const int &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const int &k){return Point(x*k,y*k);}
};
int dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
int det(Point a,Point b){return a.x*b.y-a.y*b.x;}
int Dist(Point a,Point b){return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);}
int n,k,st1[100005],st2[100005];Point p[100005];double pre[100005],suf[100005];vector<int>v[100005];
void ConvexHullPre(){
int top1=0,top2=0,ans=0;
for(int j=1;j<=2*N+1;j++){
for(auto i:v[j]){
while(top1>=2&&det(p[st1[top1]]-p[st1[top1-1]],p[i]-p[st1[top1]])<=0){
ans-=det(p[st1[top1-1]],p[st1[top1]]),top1--;
}
st1[++top1]=i;if(top1>=2)ans+=det(p[st1[top1-1]],p[st1[top1]]);
while(top2>=2&&det(p[st2[top2]]-p[st2[top2-1]],p[i]-p[st2[top2]])>=0){
ans-=det(p[st2[top2]],p[st2[top2-1]]),top2--;
}
st2[++top2]=i;if(top2>=2)ans+=det(p[st2[top2]],p[st2[top2-1]]);
}
pre[j]=abs(ans)/2.0;
}
}
void ConvexHullSuf(){
int top1=0,top2=0,ans=0;
for(int j=2*N+1;j>=1;j--){
for(auto i:v[j]){
while(top1>=2&&det(p[st1[top1]]-p[st1[top1-1]],p[i]-p[st1[top1]])<=0){
ans-=det(p[st1[top1-1]],p[st1[top1]]),top1--;
}
st1[++top1]=i;if(top1>=2)ans+=det(p[st1[top1-1]],p[st1[top1]]);
while(top2>=2&&det(p[st2[top2]]-p[st2[top2-1]],p[i]-p[st2[top2]])>=0){
ans-=det(p[st2[top2]],p[st2[top2-1]]),top2--;
}
st2[++top2]=i;if(top2>=2)ans+=det(p[st2[top2]],p[st2[top2-1]]);
}
suf[j]=abs(ans)/2.0;
}
}
signed main(){
n=read(),k=read();
for(int i=1;i<=n;i++)p[i].x=read()+N+1,p[i].y=read()+N+1,v[p[i].x].push_back(i);
for(int i=1;i<=2*N+1;i++)sort(v[i].begin(),v[i].end(),[&](int x,int y){
return p[x].y<p[y].y;
});
ConvexHullPre();
for(int i=1;i<=n;i++)p[i].x*=-1;
ConvexHullSuf();
double ans1=inf,ans2=inf;
for(int i=0;i<=2*N+1;i++){
if(ans1-fabs(fabs(pre[i]-suf[i+1])-k)>=eps){
ans1=fabs(fabs(pre[i]-suf[i+1])-k),ans2=fabs(pre[i]-suf[i+1]);
}
else if(fabs(ans1-fabs(fabs(pre[i]-suf[i+1])-k))<=eps){
if(ans2-fabs(pre[i]-suf[i+1])>=eps)ans2=fabs(pre[i]-suf[i+1]);
}
}
printf("%.4lf\n",ans2);
return 0;
}
I - Dazzling stars
有一个比较麻烦的做法,大概就是枚举一对点 \((x,y)\),因为亮的点要在上面,可以算出一个合法的旋转弧度区间,看交是否存在即可。感觉有点难实现,没写。
还有一个做法是枚举所有点对 \((x,y)\),如果 \(B_x<B_y\) 那么我们连一条 \(x\to y\) 的向量,把所有向量极角排序,如果存在一对相邻的向量夹角不小于 180 度则有解,否则无解。还有所有向量都方向相同时也有解。因为如果两个向量夹角不小于 180 度则我们让 y 轴正方向放在小于 180 度的那个夹角间即可。注意 \(a\times b\le 0\) 不代表夹角不小于 180 度,有可能 \(a,b\) 同向。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
const double eps=1e-7;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
double x,y;
Point(const double &_x=0,const double &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const double &k){return Point(x*k,y*k);}
};
double dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
double det(Point a,Point b){return a.x*b.y-a.y*b.x;}
double Len(Point a){return sqrt(dot(a,a));}
double Dist(Point a,Point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
struct Line{
Point p,way;
Line(const Point &_p=Point(0,0),const Point &_way=Point(0,0)):p(_p),way(_way){}
inline double ang(){return atan2(way.y,way.x);}
};
int OnRight(Line x,Point y){return det(x.way,y-x.p)<=-eps;}
Point Intersect(Line x,Line y){return x.p+x.way*(det(y.way,x.p-y.p)/det(x.way,y.way));}
double DistLine(Line x,Point y){return fabs(det(x.way,y-x.p))/Len(x.way);}
int x[1005],y[1005],b[1005];
signed main(){
int n=read();
for(int i=1;i<=n;i++){
x[i]=read(),y[i]=read(),b[i]=read();
}
vector<Line>p;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(b[i]>=b[j])continue;
p.push_back(Line(Point(x[i],y[i]),Point(x[j],y[j])-Point(x[i],y[i])));
}
}
sort(p.begin(),p.end(),[](Line x,Line y){
return x.ang()<y.ang();
});
int len=(int)p.size();
for(int i=0;i<len;i++){
int j=(i+1)%len;
if(det(p[i].way,p[j].way)<0||(det(p[i].way,p[j].way)==0&&dot(p[i].way,p[j].way)<0))return puts("Y"),0;
}
int flag=1;
for(int i=1;i<len;i++)if(det(p[0].way,p[i].way)!=0||dot(p[0].way,p[i].way)<0)flag=0;
if(!flag)puts("N");
else puts("Y");
return 0;
}
J - Roof Skeleton
K - Pea-City
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
const double eps=1e-7;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
double x,y;
Point(const double &_x=0,const double &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const double &k){return Point(x*k,y*k);}
};
double dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
double det(Point a,Point b){return a.x*b.y-a.y*b.x;}
double Len(Point a){return sqrt(dot(a,a));}
double Dist(Point a,Point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
struct Line{
Point p,way;double ang;
Line(const Point &_p=Point(0,0),const Point &_way=Point(0,0)):p(_p),way(_way){}
};
int OnRight(Line x,Point y){return det(x.way,y-x.p)<=-eps;}
Point Intersect(Line x,Line y){return x.p+x.way*(det(y.way,x.p-y.p)/det(x.way,y.way));}
double DistLine(Line x,Point y){return fabs(det(x.way,y-x.p))/Len(x.way);}
int st[100005],used[100005];
vector<Point>ConvexHull(vector<Point>poly){
int top=0,len=(int)poly.size();vector<Point>convex;
sort(poly.begin(),poly.end(),[](Point x,Point y){
return tie(x.x,x.y)<tie(y.x,y.y);
});
st[++top]=0;
for(int i=1;i<len;i++){
while(top>=2&&det(poly[st[top]]-poly[st[top-1]],poly[i]-poly[st[top]])<=0)top--;
st[++top]=i;
}
for(int i=1;i<=top;i++)if(!used[st[i]])convex.push_back(poly[st[i]]),used[st[i]]=1;
top=0;st[++top]=len-1;
for(int i=len-2;i>=0;i--){
while(top>=2&&det(poly[st[top]]-poly[st[top-1]],poly[i]-poly[st[top]])<=0)top--;
st[++top]=i;
}
for(int i=1;i<=top;i++)if(!used[st[i]])convex.push_back(poly[st[i]]),used[st[i]]=1;
for(int i=0;i<len;i++)used[i]=0;
return convex;
}
Point rotate(Point x){return Point(x.y,-x.x);}
double GetArea(vector<Point>poly){
int len=(int)poly.size();
if(len<=2)return 0;
double res=0;
for(int i=0;i<len;i++)res+=det(poly[i],poly[(i+1)%len]);
return fabs(res)/2;
}
vector<Point>RotatingCalipers(vector<Point>poly){
int len=(int)poly.size();vector<Point>ans;
for(int i=0,j=1,k=1,l=1;i<len;i++){
while(fabs(det(poly[(i+1)%len]-poly[i],poly[j]-poly[(i+1)%len]))<=fabs(det(poly[(i+1)%len]-poly[i],poly[(j+1)%len]-poly[(i+1)%len])))j=(j+1)%len;
l=max(l,j);
while(k!=j&&dot(poly[(i+1)%len]-poly[i],poly[(k+1)%len]-poly[k])+eps>0)k=(k+1)%len;
while(l!=i&&dot(poly[(i+1)%len]-poly[i],poly[(l+1)%len]-poly[l])-eps<0)l=(l+1)%len;
Line l1=Line(poly[i],poly[(i+1)%len]-poly[i]),l2=Line(poly[k],rotate(l1.way));
Line l3=Line(poly[j],l1.way),l4=Line(poly[l],rotate(l1.way));
vector<Point>tmp;
tmp.push_back(Intersect(l1,l2));tmp.push_back(Intersect(l2,l3));
tmp.push_back(Intersect(l3,l4));tmp.push_back(Intersect(l4,l1));
if(ans.empty()||GetArea(tmp)-eps<GetArea(ans))ans=tmp;
}
return ans;
}
signed main(){
int n=read();vector<Point>p;
for(int i=1;i<=n;i++){
double x,y;scanf("%lf%lf",&x,&y);
p.push_back(Point(x,y));
}
p=RotatingCalipers(ConvexHull(p));
for(auto x:p)printf("%.6lf %.6lf\n",x.x,x.y);
return 0;
}
L - Sunlight
单调栈扫一遍即可,因为如果 \(\dfrac{a}{b}>\dfrac{c}{d}\),那么 \(\dfrac{a}{b+x}>\dfrac{c}{d+x}\)。
点击查看代码
#define _USE_MATH_DEFINES
#include<bits/stdc++.h>
#define int long long
#define db double
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
const db pi=M_PI;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int x[200005],h[200005],q[200005];db ans[200005];
signed main(){
int n=read();
for(int i=1;i<=n;i++)x[i]=read(),h[i]=read();
for(int i=1;i<=n;i++)ans[i]=pi;
for(int i=1,top=0;i<=n;i++){
while(top>1&&(h[i]-h[q[top]])*(x[q[top]]-x[q[top-1]])>=(h[q[top]]-h[q[top-1]])*(x[i]-x[q[top]]))top--;
if(top&&h[q[top]]>=h[i])ans[i]-=atan2(h[q[top]]-h[i],x[i]-x[q[top]]);
q[++top]=i;
}
for(int i=1;i<=n;i++)x[i]=-x[i];
reverse(x+1,x+n+1);reverse(h+1,h+n+1);
for(int i=1,top=0;i<=n;i++){
while(top>1&&(h[i]-h[q[top]])*(x[q[top]]-x[q[top-1]])>=(h[q[top]]-h[q[top-1]])*(x[i]-x[q[top]]))top--;
if(top&&h[q[top]]>=h[i])ans[n-i+1]-=atan2(h[q[top]]-h[i],x[i]-x[q[top]]);
q[++top]=i;
}
for(int i=1;i<=n;i++)printf("%.5lf\n",ans[i]/pi*12.0);
return 0;
}
M - Largest Quadrilateral
题意即给若干个可能重复的点,求在这些点里任选四个构成的可能退化的四边形的面积的最大值。先求凸包,如果凸包点数不大于 2 说明答案为 0。如果凸包点数不小于 4 说明答案一定是在凸包上找一个凸四边形的面积最大值,这个可以枚举这个四边形的一条对角线然后旋转卡壳 \(\mathcal{O}(n^2)\) 求得。否则说明答案一定是一个由凸包上三个点再加一个其他点构成的凹四边形,枚举这个点算一下即可,复杂度 \(\mathcal{O}(n)\)。实现略微卡常、卡精度,比如旋转卡壳的时候判断下一个点是否更优时最好算面积比较而不是直接算点到直线的距离,否则容易掉精度。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
int x,y;
Point(const int &_x=0,const int &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const int &k){return Point(x*k,y*k);}
};
ll dot(Point a,Point b){return 1ll*a.x*b.x+1ll*a.y*b.y;}
ll det(Point a,Point b){return 1ll*a.x*b.y-1ll*a.y*b.x;}
int st[5005],used[5005];
vector<Point>ConvexHull(vector<Point>poly){
int top=0,len=(int)poly.size();vector<Point>convex;
sort(poly.begin(),poly.end(),[](Point x,Point y){
return tie(x.x,x.y)<tie(y.x,y.y);
});
st[++top]=0;
for(int i=1;i<len;i++){
while(top>=2&&det(poly[st[top]]-poly[st[top-1]],poly[i]-poly[st[top]])<=0)top--;
st[++top]=i;
}
for(int i=1;i<=top;i++)if(!used[st[i]])convex.push_back(poly[st[i]]),used[st[i]]=1;
top=0;st[++top]=len-1;
for(int i=len-2;i>=0;i--){
while(top>=2&&det(poly[st[top]]-poly[st[top-1]],poly[i]-poly[st[top]])<=0)top--;
st[++top]=i;
}
for(int i=1;i<=top;i++)if(!used[st[i]])convex.push_back(poly[st[i]]),used[st[i]]=1;
for(int i=0;i<len;i++)used[i]=0;
return convex;
}
ll GetArea(vector<Point>poly){
int len=(int)poly.size();
if(len<=2)return 0;
ll res=0;
for(int i=0;i<len;i++)res+=det(poly[i],poly[(i+1)%len]);
return abs(res);
}
ll RotatingCalipers(vector<Point>poly,vector<Point>p){
int len=(int)poly.size();
if(len<=2)return 0;
if(len==3){
int f0=0,f1=0,f2=0;ll res=0,sum=GetArea(poly);
for(auto x:p){
if(x.x==poly[0].x&&x.y==poly[0].y){
if(!f0){f0=1;continue;}
return sum;
}
if(x.x==poly[1].x&&x.y==poly[1].y){
if(!f1){f1=1;continue;}
return sum;
}
if(x.x==poly[2].x&&x.y==poly[2].y){
if(!f2){f2=1;continue;}
return sum;
}
res=max(res,sum-GetArea({poly[0],poly[1],x}));
res=max(res,sum-GetArea({poly[1],poly[2],x}));
res=max(res,sum-GetArea({poly[2],poly[0],x}));
}
return res;
}
ll res=0;
for(int i=0;i<len;i++){
for(int j=(i+2)%len,a=(i+1)%len,b=j;(j+1)%len!=i;j=(j+1)%len){
if(b==j)b=(b+1)%len;
while((a+1)%len!=j&&abs(det(poly[i],poly[a])+det(poly[a],poly[j])+det(poly[j],poly[i]))<=abs(det(poly[i],poly[(a+1)%len])+det(poly[(a+1)%len],poly[j])+det(poly[j],poly[i])))a=(a+1)%len;
while((b+1)%len!=i&&abs(det(poly[i],poly[b])+det(poly[b],poly[j])+det(poly[j],poly[i]))<=abs(det(poly[i],poly[(b+1)%len])+det(poly[(b+1)%len],poly[j])+det(poly[j],poly[i])))b=(b+1)%len;
res=max(res,abs(det(poly[i],poly[a])+det(poly[a],poly[j])+det(poly[j],poly[b])+det(poly[b],poly[i])));
}
}
return res;
}
void solve(){
int n=read();vector<Point>p;
for(int i=1;i<=n;i++){
int x=read(),y=read();
p.push_back(Point(x,y));
}
vector<Point>convex=ConvexHull(p);
ll ans=RotatingCalipers(convex,p);
if(ans%2==0)printf("%lld\n",ans/2);
else printf("%lld.5\n",ans/2);
}
signed main(){
int T=read();
while(T--){
solve();
}
return 0;
}
N - Snake
容易发现有解当且仅当对于每个拐点,我们都能找到一条穿过它的直线,使得编号在它前面和编号在它后面的点被划分成了两部分。枚举这个点,极角排序找到一对相邻的夹角不小于 180 度的向量,这条直线就在那个不小于 180 度的夹角间,判断即可。复杂度 \(\mathcal{O}(n^2\log n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
const double eps=0;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
double x,y;
Point(const double &_x=0,const double &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const double &k){return Point(x*k,y*k);}
};
double dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
double det(Point a,Point b){return a.x*b.y-a.y*b.x;}
double Len(Point a){return sqrt(dot(a,a));}
double Dist(Point a,Point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
struct Line{
Point p,way;double ang;
Line(const Point &_p=Point(0,0),const Point &_way=Point(0,0)):p(_p),way(_way){}
};
int OnRight(Line x,Point y){return det(x.way,y-x.p)<=-eps;}
Point Intersect(Line x,Line y){return x.p+x.way*(det(y.way,x.p-y.p)/det(x.way,y.way));}
double DistLine(Line x,Point y){return fabs(det(x.way,y-x.p))/Len(x.way);}
Point p[1005];
signed main(){
int n=read();
for(int i=1;i<=n;i++)p[i].x=read(),p[i].y=read();
for(int k=2;k<=n-1;k++){
vector<Line>t;
for(int i=k+1;i<=n;i++)t.push_back(Line(p[i],p[i]-p[k])),t.back().ang=atan2(t.back().way.y,t.back().way.x);
sort(t.begin(),t.end(),[](Line x,Line y){
return x.ang<y.ang;
});
if((int)t.size()>1){
int len=(int)t.size(),flag=-1;
for(int i=0;i<len;i++){
int j=(i+1)%len;
if(det(t[i].way,t[j].way)<0||(det(t[i].way,t[j].way)==0&&dot(t[i].way,t[j].way)<0)){flag=i;break;}
}
if(flag<0)return puts("Impossible"),0;
for(int i=1;i<k;i++){
if(det(t[(flag+1)%len].way,p[i]-p[k])>=0&&det(t[flag].way,p[i]-p[k])<=0)return puts("Impossible"),0;
}
}
t.clear();
for(int i=1;i<k;i++)t.push_back(Line(p[i],p[i]-p[k])),t.back().ang=atan2(t.back().way.y,t.back().way.x);
sort(t.begin(),t.end(),[](Line x,Line y){
return x.ang<y.ang;
});
if((int)t.size()>1){
int len=(int)t.size(),flag=-1;
for(int i=0;i<len;i++){
int j=(i+1)%len;
if(det(t[i].way,t[j].way)<0||(det(t[i].way,t[j].way)==0&&dot(t[i].way,t[j].way)<0)){flag=i;break;}
}
if(flag<0)return puts("Impossible"),0;
for(int i=k+1;i<=n;i++){
if(det(t[(flag+1)%len].way,p[i]-p[k])>=0&&det(t[flag].way,p[i]-p[k])<=0)return puts("Impossible"),0;
}
}
}
puts("Possible");
return 0;
}
O - Blowing Candles
先求凸包,题目所求即为凸包上一点到凸包上一条相邻点连成的直线的距离的最大值的最小值。旋转卡壳即可。复杂度 \(\mathcal{O}(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
const double eps=1e-7;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
double x,y;
Point(const double &_x=0,const double &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const double &k){return Point(x*k,y*k);}
};
double dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
double det(Point a,Point b){return a.x*b.y-a.y*b.x;}
double Len(Point a){return sqrtl(dot(a,a));}
double Dist(Point a,Point b){return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);}
struct Line{
Point p,way;double ang;
Line(const Point &_p=Point(0,0),const Point &_way=Point(0,0)):p(_p),way(_way){}
};
int OnRight(Line x,Point y){return det(x.way,y-x.p)<=-eps;}
Point Intersect(Line x,Line y){return x.p+x.way*(det(y.way,x.p-y.p)/det(x.way,y.way));}
double DistLine(Line x,Point y){return fabs(det(x.way,y-x.p))/Len(x.way);}
int n,k,st[250005],used[250005];Point p[250005];
vector<Point>ConvexHull(vector<Point>P){
int top=0,len=(int)P.size();vector<Point>convex;
sort(P.begin(),P.end(),[](Point x,Point y){
return tie(x.x,x.y)<tie(y.x,y.y);
});
st[++top]=0;
for(int i=1;i<len;i++){
while(top>=2&&det(P[st[top]]-P[st[top-1]],P[i]-P[st[top]])<=0)top--;
st[++top]=i;
}
for(int i=1;i<=top;i++)if(!used[st[i]])convex.push_back(P[st[i]]),used[st[i]]=1;
top=0;st[++top]=len-1;
for(int i=len-2;i>=0;i--){
while(top>=2&&det(P[st[top]]-P[st[top-1]],P[i]-P[st[top]])<=0)top--;
st[++top]=i;
}
for(int i=1;i<=top;i++)if(!used[st[i]])convex.push_back(P[st[i]]),used[st[i]]=1;
for(int i=0;i<len;i++)used[i]=0;
return convex;
}
double RotatingCalipers(vector<Point>P){
int len=(int)P.size();
if(len<=2)return 0;
if(len==3)return min({DistLine(Line(P[0],P[1]-P[0]),P[2]),DistLine(Line(P[1],P[2]-P[1]),P[0]),DistLine(Line(P[2],P[0]-P[2]),P[1])});
double res=inf;
for(int i=0,j=0;i<len;i++){
while(fabs(det(P[(i+1)%len]-P[i],P[j]-P[(i+1)%len]))<=fabs(det(P[(i+1)%len]-P[i],P[(j+1)%len]-P[(i+1)%len])))j=(j+1)%len;
res=min(res,DistLine(Line(P[i],P[(i+1)%len]-P[i]),P[j]));
}
return res;
}
signed main(){
n=read(),k=read();
for(int i=1;i<=n;i++)p[i].x=read(),p[i].y=read();
vector<Point>P;
for(int i=1;i<=n;i++)P.push_back(p[i]);
printf("%.7lf\n",RotatingCalipers(ConvexHull(P)));
return 0;
}
P - Kabbalah for Two
Q - Geometrical Combinatorics
刚开始有一个自然的想法是枚举每一行 \(i\),可以算出一个区间 \([l,r]\) 表示 \([l,r]\) 内的点在三角形内,求 \(\sum\limits_{i}\sum\limits_{j=l}^r\dbinom{i}{j}\) 即可。但是注意到 \(\sum\limits_{i}\dbinom{n}{i}\) 这个求和很不可做,于是寄了。
不妨换个方向思考。既然一行求和不太能行,考虑斜着枚举每一条夹角为 45 度的斜线,于是问题变成求 \(\sum\limits_{i}\sum\limits_{j=l}^r\dbinom{j}{i}\)。杨辉三角一列求和就是简单的了,直接做就行,复杂度 \(\mathcal{O}(X)\)。求 \([l,r]\) 可以算交点然后排序,注意精度。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define double long double
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18,V=1e6+5,mod=1e9+7;
const double eps=1e-9;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int jc[1000025],iv[1000025],ij[1000025];
int C(int n,int m){
if(n<0||m<0||n-m<0)return 0;
return jc[n]*ij[m]%mod*ij[n-m]%mod;
}
struct Point{
double x,y;
Point(const double &_x=0,const double &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const double &k){return Point(x*k,y*k);}
};
double dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
double det(Point a,Point b){return a.x*b.y-a.y*b.x;}
double Len(Point a){return sqrt(dot(a,a));}
double Dist(Point a,Point b){return sqrtl((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
struct Line{
Point p,way;double ang;
Line(const Point &_p=Point(0,0),const Point &_way=Point(0,0)):p(_p),way(_way){}
};
int OnRight(Line x,Point y){return det(x.way,y-x.p)<=-eps;}
Point Intersect(Line x,Line y){return x.p+x.way*(det(y.way,x.p-y.p)/det(x.way,y.way));}
double DistLine(Line x,Point y){return fabsl(det(x.way,y-x.p))/Len(x.way);}
int myfloor(double x){
return floorl(x+eps);
}
int myceil(double x){
return ceill(x-eps);
}
Point p[5];Line l[5];
void solve(){
for(int i=0;i<3;i++)p[i].x=read(),p[i].y=read();
for(int i=0;i<3;i++)l[i]=Line(p[i],p[(i+1)%3]-p[i]);
int ans=0;
for(int i=0;i<=V;i++){
Line li=Line(Point(i,i),Point(-1,1));vector<double>tmp;
for(int j=0;j<3;j++){
if(det(li.way,l[j].way)==0)continue;
Point pos=Intersect(li,l[j]);
if(fabsl(Dist(pos,p[j])+Dist(pos,p[(j+1)%3])-Dist(p[j],p[(j+1)%3]))<=eps)tmp.push_back(pos.y);
}
sort(tmp.begin(),tmp.end());
tmp.erase(unique(tmp.begin(),tmp.end(),[](double x,double y){
return fabsl(x-y)<=eps;
}),tmp.end());
if((int)tmp.size()==2){
int L=max(i,myceil(tmp[0])),R=min(V-5,myfloor(tmp[1]));
if(L>R)continue;
ans=(ans+C(R+1,i+1)-C(L,i+1)+mod)%mod;
}
else if((int)tmp.size()==1){
int x=myfloor(tmp[0]);
if(x>=i&&fabsl(x-tmp[0])<=eps)ans=(ans+C(x,i))%mod;
}
}
printf("%lld\n",ans);
}
signed main(){
jc[0]=1;for(int i=1;i<=V;i++)jc[i]=jc[i-1]*i%mod;
iv[1]=1;for(int i=2;i<=V;i++)iv[i]=mod-(mod/i)*iv[mod%i]%mod;
ij[0]=1;for(int i=1;i<=V;i++)ij[i]=ij[i-1]*iv[i]%mod;
int T=read();
while(T--){
solve();
}
return 0;
}
R - Airport Construction
P6929 [ICPC2017 WF] Airport Construction。
最开始的做法是求凸包然后旋转卡壳求最远点对,然而这个做法假得离谱,因为你没办法保证最长线段端点一定是多边形的端点,也无法保证这条线一定在多边形内。
虽然上面的做法非常假,但我们还是可以注意到一点:答案线段所在直线一定过两个多边形端点。注意到 \(n\le 200\),考虑 \(n^2\) 枚举这对点 \((i,j)\),算出 \((i,j)\) 和多边形每条边的交,把这条直线分割开后对每一段在多边形内的线段的长度求最大值。这里有一个很聪明很简单的写法:若直线与一条边不在端点上相交,根据方向不同,记交的权值为 -2 或 2,若与边的一端点相交则记为 -1 或 1。把每个交点按到 \(i\) 的有向距离从小到大排序,如果此时累加权值为 0 则表示当前在多边形外部,否则在内部。时间复杂度 \(\mathcal{O}(n^3\log n)\)。
感觉难度还好,主要是如果写的不太好可能导致代码很难写。主要是参考了这篇题解的做法,感觉非常优美。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
const double eps=1e-7;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
double x,y;
Point(const double &_x=0,const double &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const double &k){return Point(x*k,y*k);}
inline bool operator ==(const Point &b){return (fabs(x-b.x)<=eps&&fabs(y-b.y)<=eps);}
};
double dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
double det(Point a,Point b){return a.x*b.y-a.y*b.x;}
int sgn(double x){return ((fabs(x)<=eps)?0:((x<0)?-1:1));}
double Len(Point a){return sqrt(dot(a,a));}
double Dist(Point a,Point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
struct Line{
Point p,way;double ang;
Line(const Point &_p=Point(0,0),const Point &_way=Point(0,0)):p(_p),way(_way){}
};
int OnRight(Line x,Point y){return det(x.way,y-x.p)<=-eps;}
Point Intersect(Line x,Line y){return x.p+x.way*(det(y.way,x.p-y.p)/det(x.way,y.way));}
double DistLine(Line x,Point y){return fabs(det(x.way,y-x.p))/Len(x.way);}
double OnLine(Line x,Point y){return fabs(Dist(x.p,y)+Dist(x.p+x.way,y)-Len(x.way))<=eps;}
double OnLine(Point x,Point y,Point z){return fabs(Dist(x,z)+Dist(y,z)-Dist(x,y))<=eps;}
double solve(vector<Point>poly){
double res=0;
int len=(int)poly.size();
for(int i=0;i<len;i++)for(int j=i+1;j<len;j++){
Line lij=Line(poly[i],poly[j]-poly[i]);
vector<pair<double,int> >tmp;
for(int k=0;k<len;k++){
Line x=Line(poly[i],poly[k]-poly[i]);
Line y=Line(poly[i],poly[(k+1)%len]-poly[i]);
if(sgn(det(lij.way,x.way))==sgn(det(lij.way,y.way)))continue;
Point pos=Intersect(lij,Line(poly[k],poly[(k+1)%len]-poly[k]));
if(sgn(det(lij.way,x.way))<sgn(det(lij.way,y.way))){
if(pos==poly[k]||pos==poly[(k+1)%len])tmp.push_back({sgn(dot(pos-poly[i],lij.way))*Dist(pos,poly[i]),1});
else tmp.push_back({sgn(dot(pos-poly[i],lij.way))*Dist(pos,poly[i]),2});
}
else{
if(pos==poly[k]||pos==poly[(k+1)%len])tmp.push_back({sgn(dot(pos-poly[i],lij.way))*Dist(pos,poly[i]),-1});
else tmp.push_back({sgn(dot(pos-poly[i],lij.way))*Dist(pos,poly[i]),-2});
}
}
sort(tmp.begin(),tmp.end());int sum=0;double Len=0;
for(int k=0;k<(int)tmp.size();k++){
if(sum)Len+=tmp[k].first-tmp[k-1].first;
else res=max(res,Len),Len=0;
sum+=tmp[k].second;
}
res=max(res,Len);
}
return res;
}
signed main(){
int n=read();vector<Point>p;
for(int i=1,x,y;i<=n;i++){
x=read(),y=read(),p.push_back(Point(x,y));
}
printf("%.9lf\n",solve(p));
return 0;
}
S - The Jedi Killer
题意即给你三个不同的点,问是否存在一个这样的 'T' 字型图案使得三个点都在这个图案上。
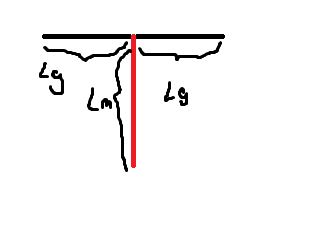
直接模拟即可,有三种情况:一个/两个/三个点在那一横上。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
const double eps=1e-7;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Point{
double x,y;
Point(const double &_x=0,const double &_y=0):x(_x),y(_y){}
inline Point operator +(const Point &o){return Point(x+o.x,y+o.y);}
inline Point operator -(const Point &o){return Point(x-o.x,y-o.y);}
inline Point operator *(const double &k){return Point(x*k,y*k);}
};
double dot(Point a,Point b){return a.x*b.x+a.y*b.y;}
double det(Point a,Point b){return a.x*b.y-a.y*b.x;}
double Len(Point a){return sqrt(dot(a,a));}
double Dist(Point a,Point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
struct Line{
Point p,way;double ang;
Line(const Point &_p=Point(0,0),const Point &_way=Point(0,0)):p(_p),way(_way){}
};
int OnRight(Line x,Point y){return det(x.way,y-x.p)<=-eps;}
Point Intersect(Line x,Line y){return x.p+x.way*(det(y.way,x.p-y.p)/det(x.way,y.way));}
double DistLine(Line x,Point y){return fabs(det(x.way,y-x.p))/Len(x.way);}
Point p[5];
void solve(){
int Lm=read(),Lg=read();
for(int i=0;i<3;i++)p[i].x=read(),p[i].y=read();
if(det(p[1]-p[0],p[2]-p[0])==0){
if(max({Dist(p[0],p[1]),Dist(p[0],p[2]),Dist(p[1],p[2])})-eps<=max(2*Lg,Lm))return puts("YES"),void();
}
for(int i=0;i<3;i++){
int j=(i+1)%3,k=(j+1)%3;
Line Lab=Line(p[i],p[j]-p[i]);
Line Lcd=Line(p[k],Point(Lab.way.y,-Lab.way.x));
Point pos=Intersect(Lab,Lcd);
double dpa=Dist(p[i],pos),dpb=Dist(p[j],pos),dpc=Dist(p[k],pos);
if(dpa-eps<=Lg&&dpb-eps<=Lg&&dpc-eps<=Lm)return puts("YES"),void();
}
for(int i=0;i<3;i++){
int j=(i+1)%3,k=(j+1)%3;
Line Lab=Line(p[i],p[j]-p[i]);
Line Lcd=Line(p[k],Point(Lab.way.y,-Lab.way.x));
Point pos=Intersect(Lab,Lcd);
double dpa=Dist(p[i],pos),dpb=Dist(p[j],pos),dpc=Dist(p[k],pos);
if((OnRight(Lcd,p[i])==OnRight(Lcd,p[j]))&&dpa-eps<=Lm&&dpb-eps<=Lm&&dpc-eps<=Lg)return puts("YES"),void();
}
puts("NO");
}
signed main(){
int T=read();
while(T--){
solve();
}
return 0;
}



