CWOI 字符串专题
A - Indie Album
考虑离线,对询问串跑 AC 自动机,建出 fail 树。再把题目中那个版本继承关系建成一棵树,在这棵树上 dfs,进入一个点的时候在 fail 树上单点加,走的时候减掉,维护子树求和即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct edge{
int v,nxt;
}e[400005];
int tot,head[400005];
void add(int u,int v){
e[++tot]=(edge){v,head[u]},head[u]=tot;
}
int I,ch[400005][28],fail[400005];
void build(){
queue<int>q;
for(int i=0;i<26;i++)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();add(fail[u],u);
for(int i=0;i<26;i++){
if(ch[u][i])fail[ch[u][i]]=ch[fail[u]][i],q.push(ch[u][i]);
else ch[u][i]=ch[fail[u]][i];
}
}
}
int cur,dfn[400005],rnk[400005],siz[400005];
vector<int>g[400005],t[400005];
struct BIT{
int c[400005];
void add(int x,int v){
for(;x<=cur;x+=x&-x)c[x]+=v;
}
void add(int l,int r,int v){
add(l,v),add(r+1,-v);
}
int ask(int x){
int res=0;
for(;x;x-=x&-x)res+=c[x];
return res;
}
int ask(int l,int r){
return ask(r)-ask(l-1);
}
}Tr;
int p[400005],ans[400005],endpos[400005];
void dfs1(int u){
dfn[u]=++cur,rnk[cur]=u,siz[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
dfs1(v);siz[u]+=siz[v];
}
}
void dfs2(int u){
Tr.add(dfn[p[u]],1);
for(auto x:t[u])ans[x]=Tr.ask(dfn[endpos[x]],dfn[endpos[x]]+siz[endpos[x]]-1);
for(auto v:g[u])dfs2(v);
Tr.add(dfn[p[u]],-1);
}
int op[400005];int x[400005],q[400005];char c[400005][5];string s[400005];
signed main(){
int n=read();
for(int i=1;i<=n;i++){
op[i]=read();
if(op[i]==1)scanf("%s",c[i]),g[0].push_back(i);
else x[i]=read(),scanf("%s",c[i]),g[x[i]].push_back(i);
}
int m=read();
for(int i=1;i<=m;i++){
q[i]=read();cin>>s[i];
}
for(int i=1;i<=m;i++){
int u=0;
for(int j=0;j<(int)s[i].size();j++){
if(!ch[u][s[i][j]-'a'])ch[u][s[i][j]-'a']=++I;
u=ch[u][s[i][j]-'a'];
}
endpos[i]=u,t[q[i]].push_back(i);
}
build();
for(int i=1;i<=n;i++){
if(op[i]==1)p[i]=ch[0][c[i][0]-'a'];
else p[i]=ch[p[x[i]]][c[i][0]-'a'];
}
dfs1(0);dfs2(0);
for(int i=1;i<=m;i++)printf("%lld\n",ans[i]);
return 0;
}
B - 通配符匹配
做烦了。
考虑按 * 把整个串分开,称为大段。把大段按 ? 分开,称为小段。先直接匹配掉最左和最右的小段。考虑安排每个大段的位置。发现越靠左越好,能为后面留下更多空间,反正中间可以用 * 一次匹配完。怎么对大段找匹配的位置呢?考虑对所有小段建 AC 自动机,从左往右扫过去,找到在 fail 树上对应的节点,然后枚举当前大段内的所有小段,如果小段能匹配当前位置的一段后缀那么就找到如果这么匹配,这个大段的开头在哪里,桶计数器加一。如果一个位置计数到了小段个数那么就说明它作为开头是合法的了。时间复杂度 \(\mathcal{O}(n|\sum|+k\sum len)\)。
细节比较多,比如没有 * 的情况要特判。其实做复杂了,只需要判断两段字符串是否相等,hash 就行。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define fi first
#define se second
using namespace std;
typedef pair<int,int>pii;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int I,ch[100005][28],fail[100005];vector<int>g[100005];
void build(){
queue<int>q;
for(int i=0;i<26;i++)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();g[fail[u]].push_back(u);
for(int i=0;i<26;i++){
if(ch[u][i])fail[ch[u][i]]=ch[fail[u]][i],q.push(ch[u][i]);
else ch[u][i]=ch[fail[u]][i];
}
}
}
int cur,dfn[100005],rnk[100005],siz[100005];
void dfs(int u){
dfn[u]=++cur,rnk[cur]=u,siz[u]=1;
for(auto v:g[u])dfs(v),siz[u]+=siz[v];
}
int n,m,endpos[15][15],check_pos[100005];
vector<int>star,ques[15];char s[100005],t[100005];
int ask(){
if(star.empty()){
if(n!=m)return 0;
for(int i=1,j=1;i<=n;i++,j++){
if(j>m)return 0;
if(s[i]=='?'||s[i]==t[j])continue;
return 0;
}
return 1;
}
for(int i=1,j=1;i<=star.front()-1;i++,j++){
if(j>m)return 0;
if(s[i]=='?'||s[i]==t[j])continue;
return 0;
}
int pos=star.front();
for(int i=0;i+1<(int)star.size();i++){
if(star[i]+1>star[i+1]-1)continue;
for(int j=1;j<=m;j++)check_pos[j]=0;
int u=0,cnt=0;
for(int k=0;k+1<(int)ques[i].size();k++){
if(ques[i][k]+1<=ques[i][k+1]-1)cnt++;
}
for(int j=pos;j<=m;j++){
u=ch[u][t[j]-'a'];
for(int k=0;k+1<(int)ques[i].size();k++){
if(ques[i][k]+1<=ques[i][k+1]-1&&dfn[endpos[i][k]]<=dfn[u]&&dfn[u]<=dfn[endpos[i][k]]+siz[endpos[i][k]]-1){
int delta=(ques[i][k+1]-1)-(ques[i][0]+1)+1;
if(j-delta+1>=1){
check_pos[j-delta+1]++;
}
}
}
}
int flag=0;
for(int j=pos;j<=m;j++){
if(check_pos[j]==cnt){
if(j+((star[i+1]-1)-(star[i]+1)+1)-1>m)return 0;
pos=j+((star[i+1]-1)-(star[i]+1)+1)-1+1;flag=1;break;
}
}
if(flag)continue;
return 0;
}
for(int i=n,j=m;i>=star.back()+1;i--,j--){
if(j<1||j<pos)return 0;
if(s[i]=='?'||s[i]==t[j])continue;
return 0;
}
return 1;
}
signed main(){
scanf("%s",s+1);n=strlen(s+1);
for(int i=1;i<=n;i++){
if(s[i]=='*')star.push_back(i);
}
for(int i=0;i+1<(int)star.size();i++){
ques[i].push_back(star[i]);
for(int j=star[i]+1;j<=star[i+1]-1;j++){
if(s[j]=='?')ques[i].push_back(j);
}
ques[i].push_back(star[i+1]);
for(int j=0;j+1<(int)ques[i].size();j++){
int u=0;
for(int k=ques[i][j]+1;k<=ques[i][j+1]-1;k++){
if(!ch[u][s[k]-'a'])ch[u][s[k]-'a']=++I;
u=ch[u][s[k]-'a'];
}
endpos[i][j]=u;
}
}
build();dfs(0);
int q=read();
while(q--){
scanf("%s",t+1);m=strlen(t+1);
if(ask())puts("YES");
else puts("NO");
}
return 0;
}
C - Death DBMS
对姓名建 AC 自动机,问题变成单点改,查询一个点到根的链上的最大值。大力树剖即可。复杂度 \(\mathcal{O}(n\log^2 n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct edge{
int v,nxt;
}e[300005];
int tot,head[300005];
void add(int u,int v){
e[++tot]=(edge){v,head[u]},head[u]=tot;
}
int I,ch[300005][28],fail[300005];
void build(){
queue<int>q;
for(int i=0;i<26;i++)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();add(fail[u],u);
for(int i=0;i<26;i++){
if(ch[u][i])fail[ch[u][i]]=ch[fail[u]][i],q.push(ch[u][i]);
else ch[u][i]=ch[fail[u]][i];
}
}
}
struct segtree{
#define ls p<<1
#define rs p<<1|1
#define lson l,mid,ls
#define rson mid+1,r,rs
struct Node{
int mx;
}c[1200005];
void pushup(int p){
c[p].mx=max(c[ls].mx,c[rs].mx);
}
void build(int l,int r,int p){
if(l==r){
c[p].mx=-1;
return;
}
int mid=(l+r)>>1;
build(lson),build(rson);
pushup(p);
}
void upd(int l,int r,int p,int x,int k){
if(l==r){c[p].mx=k;return;}
int mid=(l+r)>>1;
if(x<=mid)upd(lson,x,k);
else upd(rson,x,k);
pushup(p);
}
int qry(int l,int r,int p,int L,int R){
if(L>R)return -1;
if(L<=l&&r<=R)return c[p].mx;
int mid=(l+r)>>1,res=-1;
if(L<=mid)res=max(res,qry(lson,L,R));
if(R>mid)res=max(res,qry(rson,L,R));
return res;
}
#undef ls
#undef rs
#undef lson
#undef rson
}Tr;
int siz[300005],son[300005],dep[300005];
void dfs1(int u){
siz[u]=1,son[u]=-1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;dep[v]=dep[u]+1;
dfs1(v);siz[u]+=siz[v];
if(son[u]==-1||siz[son[u]]<siz[v])son[u]=v;
}
}
int cur,dfn[300005],rnk[300005],top[300005];
void dfs2(int u,int rt){
top[u]=rt,dfn[u]=++cur,rnk[cur]=u;
if(son[u]!=-1)dfs2(son[u],rt);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v!=son[u])dfs2(v,v);
}
}
int endpos[300005],a[300005];string s[300005];multiset<int>S[300005];
int ask(int u,int v){
int res=-1;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);
res=max(res,Tr.qry(1,cur,1,dfn[top[u]],dfn[u]));
u=fail[top[u]];
}
if(dep[u]<dep[v])swap(u,v);
res=max(res,Tr.qry(1,cur,1,dfn[v],dfn[u]));
return res;
}
signed main(){
int n=read(),m=read();
for(int i=1;i<=n;i++){
int u=0;cin>>s[i];
for(int j=0;j<(int)s[i].size();j++){
if(!ch[u][s[i][j]-'a'])ch[u][s[i][j]-'a']=++I;
u=ch[u][s[i][j]-'a'];
}
endpos[i]=u,a[i]=0;
}
build();dfs1(0);dfs2(0,0);Tr.build(1,cur,1);
for(int i=0;i<=I;i++)S[i].insert(-1);
for(int i=1;i<=n;i++)S[endpos[i]].insert(a[i]),Tr.upd(1,cur,1,dfn[endpos[i]],0);
while(m--){
int op=read();
if(op==1){
int x=read(),y=read();
S[endpos[x]].erase(S[endpos[x]].find(a[x]));
a[x]=y;S[endpos[x]].insert(a[x]);
Tr.upd(1,cur,1,dfn[endpos[x]],*S[endpos[x]].rbegin());
}
else{
int u=0,res=-1;string q;cin>>q;
for(int i=0;i<(int)q.size();i++){
u=ch[u][q[i]-'a'];
res=max(res,ask(0,u));
}
printf("%lld\n",res);
}
}
return 0;
}
D - 喵星球上的点名
本题正解似乎是广义 sam 或者 sa 之类的玩意,但可以不用。考虑一个经典结论:模式串的长度种类是 \(\sqrt{\sum len}\) 级别的。于是你可以对每种长度开一个哈希表,暴力枚举长度 hash 找模式串就是 \(\mathcal{O}(\sum len\sqrt{\sum len})\) 的了。
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
using namespace std;
const int N=1e5;
const ull base=13331;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
unordered_map<ull,int>buc[325],tmp[325];
struct Node{
int len;vector<int>s;vector<ull>h;
}a[2][50005],b[100005];
int n,m,tot,ans1[100005],ans2[50005],B[100005];ull pw[100005];
void solve(int id){
for(int i=1;i<=tot;i++){
unordered_map<ull,int>c;
for(int j=1;j+B[i]-1<=a[0][id].len;j++){
if(buc[i].count((ull)(a[0][id].h[j+B[i]-1]-a[0][id].h[j-1]*pw[B[i]]))){
c[(ull)(a[0][id].h[j+B[i]-1]-a[0][id].h[j-1]*pw[B[i]])]=1;
}
}
for(int j=1;j+B[i]-1<=a[1][id].len;j++){
if(buc[i].count((ull)(a[1][id].h[j+B[i]-1]-a[1][id].h[j-1]*pw[B[i]]))){
c[(ull)(a[1][id].h[j+B[i]-1]-a[1][id].h[j-1]*pw[B[i]])]=1;
}
}
for(auto x:c)ans2[id]+=buc[i][x.first],tmp[i][x.first]++;
}
}
signed main(){
n=read(),m=read();
pw[0]=1;for(int i=1;i<=N;i++)pw[i]=pw[i-1]*base;
for(int i=1;i<=n;i++){
for(int o=0;o<2;o++){
int k=read();a[o][i].len=k;
a[o][i].s.resize(k+5);for(int j=1;j<=k;j++)a[o][i].s[j]=read()+1;
a[o][i].h.resize(k+5);for(int j=1;j<=k;j++)a[o][i].h[j]=a[o][i].h[j-1]*base+a[o][i].s[j];
}
}
for(int i=1;i<=m;i++){
int k=read();b[i].len=k;B[++tot]=k;
b[i].s.resize(k+5);for(int j=1;j<=k;j++)b[i].s[j]=read()+1;
b[i].h.resize(k+5);for(int j=1;j<=k;j++)b[i].h[j]=b[i].h[j-1]*base+b[i].s[j];
}
sort(B+1,B+tot+1);tot=unique(B+1,B+tot+1)-B-1;
for(int i=1;i<=m;i++){
b[i].len=lower_bound(B+1,B+tot+1,b[i].len)-B;
buc[b[i].len][b[i].h[B[b[i].len]]]++;
}
for(int i=1;i<=n;i++)solve(i);
for(int i=1;i<=m;i++)ans1[i]=tmp[b[i].len][b[i].h[B[b[i].len]]];
for(int i=1;i<=m;i++)printf("%d\n",ans1[i]);
for(int i=1;i<=n;i++)printf("%d ",ans2[i]);
return 0;
}
一个正经的 \(\mathcal{O}(\sum len(\log\sum len+\log|\sum|))\) 的做法。
首先一个串可能既在姓里也在名里,考虑把姓名拼起来,中间插一个字符集中不存在的字符,只需要判断一个串在不在我们连成的新串里面就可以不重不漏了。考虑对询问串建 AC 自动机。注意到普通的 AC 自动机建法时空复杂度都是 \(\sum len|\sum|\) 的,这显然不能接受。注意到我们在建 AC 自动机时,一个点 \(u\) 如果有对应转移我们会保留,没有则会继承 \(fail(u)\) 的转移。考虑用主席树维护转移,每次直接把 \(fail(u)\) 的所有转移复制过来,然后再把它自己有的转移改上去。
考虑怎么求答案。第一个问题问有多少个姓名包含给定串。考虑对每个姓名的每个前缀在 fail 树上对应的点找出来,覆盖它们到根的路径,单点查询一个点被覆盖了几次(一个姓名的覆盖只算一次)。先把这个变成单点加子树求和。然后为了不算重我们把一个姓名的所有点按 dfs 序排序,然后减去相邻两点的 lca 的贡献即可。第二个问题可以变成子树加单点求和,也可以用上面的办法减去重复贡献。
似乎还有 GSAM 的做法,看什么时候会了补一下。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define fi first
#define se second
using namespace std;
typedef pair<int,int>pii;
const int inf=1e4+1;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct segtree{
#define ls (c[p].lc)
#define rs (c[p].rc)
#define lson l,mid,ls
#define rson mid+1,r,rs
struct Node{
int lc,rc,s;
}c[4000005];
int T;
void pushup(int p){
c[p].s=c[ls].s+c[rs].s;
}
int build(int l,int r){
int p=++T;
if(l==r){c[p].s=0;return p;}
int mid=(l+r)>>1;
ls=build(l,mid);rs=build(mid+1,r);
pushup(p);return p;
}
int upd(int l,int r,int q,int x,int v){
int p=++T;c[p]=c[q];
if(l==r){c[p].s=v;return p;}
int mid=(l+r)>>1;
if(x<=mid)ls=upd(l,mid,c[q].lc,x,v);
else rs=upd(mid+1,r,c[q].rc,x,v);
pushup(p);return p;
}
int ask(int l,int r,int p,int x){
if(l==r)return c[p].s;
int mid=(l+r)>>1;
if(x<=mid)return ask(lson,x);
else return ask(rson,x);
}
#undef lson
#undef rson
#undef ls
#undef rs
}Tr;
int I,root[100005],fail[100005];vector<pii>trans[100005];vector<int>g[100005];
void buildAC(){
queue<int>q;
for(int i=0;i<=inf;i++)if(Tr.ask(0,inf,root[0],i))q.push(Tr.ask(0,inf,root[0],i));
while(!q.empty()){
int u=q.front();q.pop();g[fail[u]].push_back(u);root[u]=root[fail[u]];
for(auto v:trans[u]){
root[u]=Tr.upd(0,inf,root[u],v.fi,v.se);
fail[v.se]=Tr.ask(0,inf,root[fail[u]],v.fi);
q.push(v.se);
}
}
}
int cur,dfn[100005],f[20][100005],siz[100005];
int getmin(int u,int v){
return ((dfn[u]<dfn[v])?u:v);
}
void dfs(int u){
dfn[u]=++cur,f[0][cur]=fail[u],siz[u]=1;
for(auto v:g[u])dfs(v),siz[u]+=siz[v];
}
int getlca(int u,int v){
if(u==v)return u;
if((u=dfn[u])>(v=dfn[v]))swap(u,v);
int o=__lg(v-u++);
return getmin(f[o][u],f[o][v-(1ll<<o)+1]);
}
struct BIT{
int c[100005];
void clear(){
for(int i=1;i<=cur;i++)c[i]=0;
}
void add(int x,int v){
for(;x<=cur;x+=x&-x)c[x]+=v;
}
void add(int l,int r,int v){
add(l,v),add(r+1,-v);
}
int ask(int x){
int res=0;
for(;x;x-=x&-x)res+=c[x];
return res;
}
int ask(int l,int r){
return ask(r)-ask(l-1);
}
}bit;
int pos[100005];vector<int>a[100005],b[100005];
signed main(){
int n=read(),m=read();
for(int i=1,len;i<=n;i++){
len=read();
for(int j=1;j<=len;j++)a[i].push_back(read());
a[i].push_back(inf);
len=read();
for(int j=1;j<=len;j++)a[i].push_back(read());
}
for(int i=1,len;i<=m;i++){
len=read();
for(int j=1;j<=len;j++)b[i].push_back(read());
}
root[0]=Tr.build(0,inf);
for(int i=1;i<=m;i++){
int u=0;
for(auto j:b[i]){
if(!Tr.ask(0,inf,root[u],j))root[u]=Tr.upd(0,inf,root[u],j,++I),trans[u].push_back({j,I});
u=Tr.ask(0,inf,root[u],j);
}
pos[i]=u;
}
buildAC();dfs(0);
for(int j=1;(1ll<<j)<=cur;j++){
for(int i=1;i+(1ll<<j)-1<=cur;i++){
f[j][i]=getmin(f[j-1][i],f[j-1][i+(1ll<<(j-1))]);
}
}
for(int i=1;i<=n;i++){
int u=0;vector<int>tmp;
for(auto j:a[i])u=Tr.ask(0,inf,root[u],j),tmp.push_back(u);
sort(tmp.begin(),tmp.end(),[](int x,int y){return dfn[x]<dfn[y];});
for(int j=0;j<(int)tmp.size();j++)bit.add(dfn[tmp[j]],1);
for(int j=1;j<(int)tmp.size();j++)bit.add(dfn[getlca(tmp[j-1],tmp[j])],-1);
}
for(int i=1;i<=m;i++){
printf("%lld\n",bit.ask(dfn[pos[i]],dfn[pos[i]]+siz[pos[i]]-1));
}
bit.clear();
for(int i=1;i<=m;i++)bit.add(dfn[pos[i]],dfn[pos[i]]+siz[pos[i]]-1,1);
for(int i=1;i<=n;i++){
int u=0,res=0;vector<int>tmp;
for(auto j:a[i])u=Tr.ask(0,inf,root[u],j),tmp.push_back(u);
sort(tmp.begin(),tmp.end(),[](int x,int y){return dfn[x]<dfn[y];});
for(int j=0;j<(int)tmp.size();j++)res+=bit.ask(dfn[tmp[j]]);
for(int j=1;j<(int)tmp.size();j++)res-=bit.ask(dfn[getlca(tmp[j-1],tmp[j])]);
printf("%lld ",res);
}
return 0;
}
F - 双倍回文
考虑 manacher。容易发现因为我们只需要统计最长的双倍回文串,所以只有在当前位置拓展得超过最大右边界时才有可能更新答案,复杂度 \(\mathcal{O}(n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int r[1000005];char s[1000005],t[1000005];
signed main(){
int m=read(),n=0,ans=0,c=0,R=0;scanf("%s",t+1);s[0]='!',s[++n]='#';
for(int i=1;i<=m;i++)s[++n]=t[i],s[++n]='#';
for(int i=1;i<=n;i++){
r[i]=((i<=R)?min(r[2*c-i],R-i+1):0ll);
while(i-r[i]>=1&&s[i-r[i]]==s[i+r[i]])r[i]++;
if(i+r[i]-1>R){
for(int j=R+1;j<=i+r[i]-1;j++){
if((j&1ll)&&(j-i)%4==0&&r[(i+(i*2-j))/2]>=(j-i)/2)ans=max(ans,j-i);
}
c=i,R=i+r[i]-1;
}
}
printf("%lld\n",ans);
return 0;
}
G - Palindromic Substring
经典结论:串 \(S\) 的本质不同回文子串个数不超过 \(|S|\)。manacher,每次拓展的时候把这些回文串找出来。注意此时这些串可能有重复,需要去重。问题变成有一些区间 \([l,r]\),问 \(s[l\ldots r]\) 在 \(s\) 中出现了几次。对 \(s\) 跑 SA,对于询问 \([l,r]\),向左/右二分出能包含 \([l,r]\) 的最长位置。每次询问把所有串的价值排序即可。复杂度 \(\mathcal{O}(Tmn\log n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18,mod=777777777;
const ull base=13331;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int rk[200005],sa[200005],c[200005],tp[200005],ht[200005];char s[200005],t[200005];
int cmp(int x,int y,int w){
return (tp[x]==tp[y]&&tp[x+w]==tp[y+w]);
}
void buildSA(int n){
int m='z';
for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int w=1,p=0;;w<<=1){
for(int i=n;i>=n-w+1;i--)tp[++p]=i;
for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int i=1;i<=n;i++)tp[i]=rk[i];
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)rk[sa[i]]=(cmp(sa[i-1],sa[i],w)?p:++p);
if(p==n)break;
m=p,p=0;
}
}
int f[20][200005];
int ask(int l,int r){
assert(l<=r);
int o=__lg(r-l+1);
return min(f[o][l],f[o][r-(1ll<<o)+1]);
}
int r[200005],lp[200005],rp[200005],cnt[200005];
int PW[200005],sum[200005],val[30],w[200005],id[200005];
int get(int l,int r){
return (sum[r]-sum[l-1]*PW[r-l+1]%mod+mod)%mod;
}
ull pw[200005],h[200005];
void solve(){
int n=read(),m=read(),len=0,tot=0;
scanf("%s",s+1);t[0]='!',t[++len]='#';
for(int i=1;i<=n;i++)t[++len]=s[i],t[++len]='#';
int p=0,R=0;
for(int i=1;i<=len;i++){
r[i]=((i<=R)?min(r[2*p-i],R-i+1):0ll);
while(i-r[i]>=1&&t[i-r[i]]==t[i+r[i]])r[i]++;
if(i+r[i]-1>R){
for(int j=R+1;j<=i+r[i]-1;j++){
if('a'<=t[j]&&t[j]<='z'){
lp[++tot]=(2*i-j)/2,rp[tot]=j/2,cnt[tot]=0;
}
}
p=i,R=i+r[i]-1;
}
}
pw[0]=1;for(int i=1;i<=n;i++)h[i]=h[i-1]*base+s[i],pw[i]=pw[i-1]*base;
map<ull,int>vis;vector<int>tmp;
for(int i=1;i<=tot;i++){
if(!vis[h[rp[i]]-h[lp[i]-1]*pw[rp[i]-lp[i]+1]]){
vis[h[rp[i]]-h[lp[i]-1]*pw[rp[i]-lp[i]+1]]=1;
tmp.push_back(i);
}
}
tot=0;
for(auto x:tmp)lp[++tot]=lp[x],rp[tot]=rp[x];
buildSA(n);
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1){ht[rk[i]]=0;continue;}
if(k)k--;
while(s[i+k]==s[sa[rk[i]-1]+k])k++;
ht[rk[i]]=k;
}
for(int i=1;i<=n;i++)f[0][i]=ht[i];
for(int j=1;(1ll<<j)<=n;j++){
for(int i=1;i+(1ll<<j)-1<=n;i++){
f[j][i]=min(f[j-1][i],f[j-1][i+(1ll<<(j-1))]);
}
}
for(int i=1,l,r,res;i<=tot;i++){
l=rk[lp[i]]+1,r=n,res=rk[lp[i]];cnt[i]=0;
while(l<=r){
int mid=(l+r)>>1;
if(ask(rk[lp[i]]+1,mid)>=rp[i]-lp[i]+1)res=mid,l=mid+1;
else r=mid-1;
}
cnt[i]+=res-rk[lp[i]]+1;
l=1,r=rk[lp[i]]-1,res=rk[lp[i]];
while(l<=r){
int mid=(l+r)>>1;
if(ask(mid+1,rk[lp[i]])>=rp[i]-lp[i]+1)res=mid,r=mid-1;
else l=mid+1;
}
cnt[i]+=rk[lp[i]]-res;
}
PW[0]=1;for(int i=1;i<=n;i++)PW[i]=PW[i-1]*26%mod;
while(m--){
int k=read();
for(int i=0;i<26;i++)val[i]=read();
for(int i=1;i<=n;i++)sum[i]=(sum[i-1]*26%mod+val[s[i]-'a'])%mod;
for(int i=1;i<=tot;i++)w[i]=get(lp[i],(lp[i]+rp[i])/2);
for(int i=1;i<=tot;i++)id[i]=i;
sort(id+1,id+tot+1,[](int x,int y){return w[x]<w[y];});
int flag=0;
for(int i=1;i<=tot;i++){
if(k>cnt[id[i]])k-=cnt[id[i]];
else{printf("%lld\n",w[id[i]]);flag=1;break;}
}
if(!flag)puts("0");
}
for(int i=0;i<=len;i++)rk[i]=sa[i]=tp[i]=ht[i]=f[0][i]=0;
for(int i=0;i<=len;i++)r[i]=lp[i]=rp[i]=cnt[i]=w[i]=pw[i]=PW[i]=h[i]=sum[i]=id[i]=t[i]=0;
puts("");
}
signed main(){
int T=read();
while(T--){
solve();
}
return 0;
}
H - Palindromic Equivalence
牛牛题。考虑 manacher,对于一个回文串 \([l,r]\),注意到它能提供的信息是回文串内对应的位置在新串内也要相等,然后 \(l-1\) 和 \(r+1\) 不等。相等关系我们并查集合并,不等关系我们先放着。容易发现只有在 manacher 拓展的时候才用合并。
对于并查集的一个连通块,考虑其中编号最小的一个点,将这个点的编号当成这个连通块的编号。假如现在 \(i<j<k\) 三个连通块满足 \((i,k)\) 和 \((j,k)\) 间都有不等关系,注意到此时 \((i,j)\) 间也一定有不等关系。证明就是你发现 \((i,k)\) 和 \((j,k)\) 间都是一个极长的回文串,所以你把 \((j,k)\) 翻到左边,记作 \(j'\)。大概长这样:
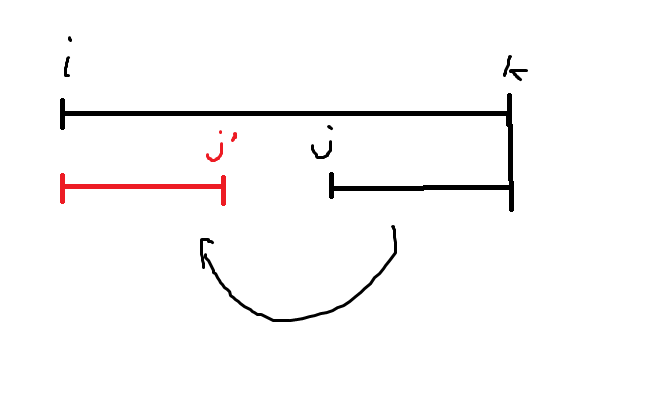
但是你注意到如果长成这样的话那么 \(j'\) 和 \(j\) 实际上是相等关系,如果此时 \(i\) 和 \(j\) 也是相等关系的话,那左边就不是一个极长的回文串,与定义不符。还有一种情况是:
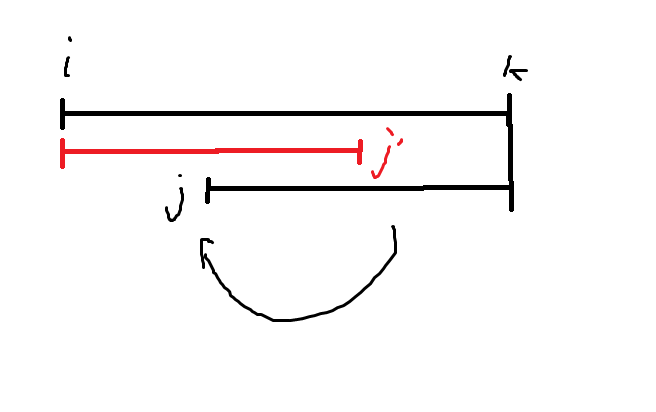
这其实也是能得到 \(j'\) 和 \(j\) 是相等关系,所以 \(i\) 和 \(j\) 只能是不等关系。
综上所述,我们从小到大枚举每个连通块 \(i\),看它和之前的哪些连通块有连边,记为 \(S\)。那么根据上述结论,\(i\) 和 \(S\) 中所有连通块的颜色都不同,所以选法就是 \(26-|S|\)。复杂度 \(\mathcal{O}(n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18,mod=1e9+7;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int fa[1000005],r[2000005],vis[1000005];vector<int>g[1000005];char s[2000005],t[2000005];
int find(int x){
return ((x==fa[x])?x:fa[x]=find(fa[x]));
}
void merge(int x,int y){
if((x=find(x))==(y=find(y)))return;
fa[y]=x;
}
signed main(){
scanf("%s",t+1);int m=strlen(t+1),n=0,ans=1;s[0]='!',s[++n]='#';
for(int i=1;i<=m;i++)s[++n]=t[i],s[++n]='#',fa[i]=i;
vector<pair<int,int> >tmp;
for(int i=1,c=0,R=0;i<=n;i++){
r[i]=((i<=R)?min(r[2*c-i],R-i+1):0ll);
while(i-r[i]>=1&&i+r[i]<=n&&s[i-r[i]]==s[i+r[i]]){
if((i-r[i])%2==0)merge((i-r[i])/2,(i+r[i])/2);
r[i]++;
}
if(i-r[i]>=1&&i+r[i]<=n)tmp.push_back({(i-r[i])/2,(i+r[i])/2});
if(i+r[i]-1>R)c=i,R=i+r[i]-1;
}
for(auto x:tmp){
int u=min(find(x.first),find(x.second));
int v=max(find(x.first),find(x.second));
g[v].push_back(u);
}
for(int i=1;i<=m;i++){
if(find(i)==i){
int cnt=26;
for(auto x:g[i])if(!vis[x])cnt--,vis[x]=1;
for(auto x:g[i])vis[x]=0;
ans=ans*cnt%mod;
}
}
printf("%lld\n",ans);
return 0;
}
I - 不同子串个数
考虑直接跑 SA,然后求 height 数组。这个不同子串个数其实就是对每个后缀建 trie,求 trie 的大小。考虑从小到大枚举 \(i\),考虑相邻的 \(sa(i-1),sa(i)\) 的 lca 的深度是 \(height(i)\),直接把这重复的一段减去即可。即 \(\sum (n-sa(i)+1-height(i))\)。复杂度 \(\mathcal{O}(n\log n)\),瓶颈在于 SA。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int n,m,rk[200005],c[200005],sa[200005],tp[200005],ht[200005];char s[100005];
int cmp(int x,int y,int w){
return (tp[x]==tp[y]&&tp[x+w]==tp[y+w]);
}
void buildSA(){
int m='z';
for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int w=1,p=0;;w<<=1){
for(int i=n;i>=n-w+1;i--)tp[++p]=i;
for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int i=1;i<=n;i++)tp[i]=rk[i];
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)rk[sa[i]]=(cmp(sa[i-1],sa[i],w)?p:++p);
if(p==n)break;
m=p,p=0;
}
}
signed main(){
n=read();scanf("%s",s+1);buildSA();
for(int i=1,k=0;i<=n;i++){
if(rk[i]==0)continue;
if(k)--k;
while(s[i+k]==s[sa[rk[i]-1]+k])k++;
ht[rk[i]]=k;
}
int ans=0;
for(int i=1;i<=n;i++){
ans+=n-sa[i]+1-ht[i];
}
printf("%lld\n",ans);
return 0;
}
可以算是 sam 的基本应用。建出 sam,答案即为 sam 上不同路径条数,拓扑一下即可。
J - 弦论
对于 \(t=0\) 很简单,直接 SA 就行,难点在于 \(t=1\)。如果我们直接模仿 \(t=0\) 的做法,找到第一个 \(\sum n-sa(i)+1>k\) 的位置的话,会发现这样求出来的答案会偏大,因为后面可能还有更小的前缀。考虑把此时这个串的真实排名表示出来,假设这是排名为 \(p\) 的后缀的长为 \(l\) 的前缀,那么 \(rank(p,l)=(\sum\limits_{i=1}^{p-1}n-sa(i)+1)+l+(\sum\limits_{i=p+1}^n\min(l,\min\limits_{j=p+1}^i\{height(j)\}))\)。容易发现一个串在 \(t=0\) 时的排名增加,它在 \(t=1\) 时的排名也会增加,于是就可以二分答案在 \(t=0\) 时的排名。复杂度 \(\mathcal{O}(n\log n+n\log k)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int n,m,rk[1000005],c[1000005],sa[1000005],tp[1000005],ht[1000005];char s[1000005];
int cmp(int x,int y,int w){
return (tp[x]==tp[y]&&tp[x+w]==tp[y+w]);
}
void buildSA(){
int m='z';
for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int w=1,p=0;;w<<=1){
for(int i=n;i>=n-w+1;i--)tp[++p]=i;
for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int i=1;i<=n;i++)tp[i]=rk[i];
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)rk[sa[i]]=(cmp(sa[i-1],sa[i],w)?p:++p);
if(p==n)break;
m=p,p=0;
}
}
int f[21][500005];
int ask(int l,int r){
if(l>r)return inf;
int o=__lg(r-l+1);
return min(f[o][l],f[o][r-(1ll<<o)+1]);
}
int check(int mid,int k){
int sum=0,pos=0,len=0;
for(int i=1;i<=n;i++){
if(sum+n-sa[i]+1-ht[i]>=mid){pos=i,len=mid-sum+ht[i];break;}
sum+=n-sa[i]+1-ht[i];
}
if(pos==0)return 0;
int cnt=len;
for(int i=1;i<pos;i++)cnt+=n-sa[i]+1;
for(int i=pos+1;i<=n;i++)cnt+=min(len,ask(pos+1,i));
return (cnt>=k);
}
signed main(){
scanf("%s",s+1);n=strlen(s+1);buildSA();
for(int i=1,k=0;i<=n;i++){
if(rk[i]==0)continue;
if(k)--k;
while(s[i+k]==s[sa[rk[i]-1]+k])k++;
ht[rk[i]]=k;
}
int t=read(),k=read();
if(t==0){
int sum=0;
for(int i=1;i<=n;i++){
if(sum+n-sa[i]+1-ht[i]>=k){
for(int j=sa[i];j<=sa[i]+k-sum-1+ht[i];j++)printf("%c",s[j]);
return 0;
}
sum+=n-sa[i]+1-ht[i];
}
puts("-1");
}
else{
if(k>n*(n+1)/2)return puts("-1"),0;
for(int i=1;i<=n;i++)f[0][i]=ht[i];
for(int j=1;(1ll<<j)<=n;j++){
for(int i=1;i+(1ll<<j)-1<=n;i++){
f[j][i]=min(f[j-1][i],f[j-1][i+(1ll<<(j-1))]);
}
}
int l=1,r=k,res=0;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid,k))res=mid,r=mid-1;
else l=mid+1;
}
int sum=0;
for(int i=1;i<=n;i++){
if(sum+n-sa[i]+1-ht[i]>=res){
for(int j=sa[i];j<=sa[i]+res-sum-1+ht[i];j++)printf("%c",s[j]);
return 0;
}
sum+=n-sa[i]+1-ht[i];
}
}
return 0;
}
K - 字符串
考虑二分答案 \(mid\),现在需要判断 \(\max\limits_{i=a}^{b-mid+1}\{\text{lcp}(s[i\ldots n],s[c\ldots d])\}\) 是否不小于 \(mid\)。考虑再次二分出满足条件的 \(i\) 的排名对应的区间,问题变成判断区间内是否存在一段区间内的数,主席树即可,复杂度 \(\mathcal{O}(n\log^2 n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int n,q,rk[200005],c[200005],sa[200005],tp[200005],ht[200005];char s[100005];
int cmp(int x,int y,int w){
return (tp[x]==tp[y]&&tp[x+w]==tp[y+w]);
}
void buildSA(){
int m='z';
for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int w=1,p=0;;w<<=1){
for(int i=n;i>=n-w+1;i--)tp[++p]=i;
for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int i=1;i<=n;i++)tp[i]=rk[i];
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)rk[sa[i]]=(cmp(sa[i-1],sa[i],w)?p:++p);
if(p==n)break;
m=p,p=0;
}
}
int root[100005];
struct segtree{
#define ls (c[p].lc)
#define rs (c[p].rc)
#define lson l,mid,ls
#define rson mid+1,r,rs
struct Node{
int lc,rc,s;
}c[3000005];
int T,root[100005];
void pushup(int p){
c[p].s=c[ls].s+c[rs].s;
}
int build(int l,int r){
int p=++T;
if(l==r){c[p].s=0;return p;}
int mid=(l+r)>>1;
ls=build(l,mid);rs=build(mid+1,r);
pushup(p);return p;
}
int add(int l,int r,int q,int x,int k){
int p=++T;c[p]=c[q];
if(l==r){c[p].s+=k;return p;}
int mid=(l+r)>>1;
if(x<=mid)ls=add(l,mid,c[q].lc,x,k);
else rs=add(mid+1,r,c[q].rc,x,k);
pushup(p);return p;
}
int ask(int l,int r,int p,int q,int L,int R){
if(L>R)return 0;
if(L<=l&&r<=R){
return c[q].s-c[p].s;
}
int mid=(l+r)>>1,res=0;
if(L<=mid)res+=ask(lson,c[q].lc,L,R);
if(R>mid)res+=ask(rson,c[q].rc,L,R);
return res;
}
#undef lson
#undef rson
#undef ls
#undef rs
}Tr;
int f[20][100005];
int ask(int l,int r){
if(l>r)return inf;
int o=__lg(r-l+1);
return min(f[o][l],f[o][r-(1ll<<o)+1]);
}
int check(int len,int a,int b,int c,int d){
if(a<=c&&c<=b-len+1)return 1;
int l=1,r=rk[c]-1,res=-1;
while(l<=r){
int mid=(l+r)>>1;
if(ask(mid+1,rk[c])>=len)res=mid,r=mid-1;
else l=mid+1;
}
if(res!=-1&&Tr.ask(1,n,root[a-1],root[b-len+1],res,rk[c]-1))return 1;
l=rk[c]+1,r=n,res=-1;
while(l<=r){
int mid=(l+r)>>1;
if(ask(rk[c]+1,mid)>=len)res=mid,l=mid+1;
else r=mid-1;
}
if(res!=-1&&Tr.ask(1,n,root[a-1],root[b-len+1],rk[c]+1,res))return 1;
return 0;
}
signed main(){
n=read(),q=read();
scanf("%s",s+1);buildSA();
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1){ht[rk[i]]=0;continue;}
if(k)k--;
while(s[i+k]==s[sa[rk[i]-1]+k])k++;
ht[rk[i]]=k;
}
for(int i=1;i<=n;i++)f[0][i]=ht[i];
for(int j=1;(1ll<<j)<=n;j++){
for(int i=1;i+(1ll<<j)-1<=n;i++){
f[j][i]=min(f[j-1][i],f[j-1][i+(1ll<<(j-1))]);
}
}
root[0]=Tr.build(1,n);
for(int i=1;i<=n;i++)root[i]=Tr.add(1,n,root[i-1],rk[i],1);
while(q--){
int a=read(),b=read(),c=read(),d=read();
int l=1,r=min(b-a+1,d-c+1),res=0;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid,a,b,c,d))res=mid,l=mid+1;
else r=mid-1;
}
printf("%lld\n",res);
}
return 0;
}
L - 优秀的拆分
考虑怎么统计答案。统计每个位置 \(i\) 成为形如 AA 的开头/结尾的次数,记作 \(a_i,b_i\),那么答案就是 \(\sum b_ia_{i+1}\)。如果直接 \(\mathcal{O}(n^2)\) 枚举每个串然后 hash 判断的话可以得 95pts。
正解基于一个很智慧的结论。考虑枚举这些串的长度 \(2len\),注意到如果我们把所有编号为 \(len\) 的倍数的点打上标记的话,一个 AA 串上一定会有刚好两个标记。不妨在这两个标记点 \(i\) 和 \(j\) 上统计这个串。可以枚举这个串在 \(i\) 及之前的长度 \(x\) 和 \(j\) 之后的长度 \(y\),有 \(x+y=len\),且 \(1\le x\le\text{lcs}(s[1\ldots i],s[1\ldots j])\),\(0\le y\le\text{lcp}(s[i+1\ldots n],s[j+1\ldots n])\)。注意到合法的左端点只会是一段区间,后缀数组预处理后算一下即可。复杂度 \(\mathcal{O}(n\log n+n\ln n)\)。
注意数组不要忘了清空,比如 \(tp\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int n,rk[120005],c[120005],sa[120005],tp[120005],ht[120005];char s[120005];
int cmp(int x,int y,int w){
return (tp[x]==tp[y]&&tp[x+w]==tp[y+w]);
}
void buildSA(){
int m='z';
for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int w=1,p=0;;w<<=1){
for(int i=n;i>=n-w+1;i--)tp[++p]=i;
for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int i=1;i<=n;i++)tp[i]=rk[i];
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)rk[sa[i]]=(cmp(sa[i-1],sa[i],w)?p:++p);
if(p==n)break;
m=p,p=0;
}
}
int f[20][60005],g[20][60005];
int askf(int l,int r){
if(l>r)return 0;
int o=__lg(r-l+1);
return min(f[o][l],f[o][r-(1ll<<o)+1]);
}
int askg(int l,int r){
if(l>r)return 0;
int o=__lg(r-l+1);
return min(g[o][l],g[o][r-(1ll<<o)+1]);
}
int rk1[120005],rk2[120005],a[120005],b[120005];
void solve(){
scanf("%s",s+1);n=strlen(s+1);buildSA();
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1){ht[rk[i]]=0;continue;}
if(k)k--;
while(s[i+k]==s[sa[rk[i]-1]+k])k++;
ht[rk[i]]=k;
}
for(int i=1;i<=n;i++)f[0][i]=ht[i];
for(int j=1;(1ll<<j)<=n;j++){
for(int i=1;i+(1ll<<j)-1<=n;i++){
f[j][i]=min(f[j-1][i],f[j-1][i+(1ll<<(j-1))]);
}
}
for(int i=1;i<=n;i++)rk1[i]=rk[i];
reverse(s+1,s+n+1);buildSA();
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1){ht[rk[i]]=0;continue;}
if(k)k--;
while(s[i+k]==s[sa[rk[i]-1]+k])k++;
ht[rk[i]]=k;
}
for(int i=1;i<=n;i++)g[0][i]=ht[i];
for(int j=1;(1ll<<j)<=n;j++){
for(int i=1;i+(1ll<<j)-1<=n;i++){
g[j][i]=min(g[j-1][i],g[j-1][i+(1ll<<(j-1))]);
}
}
for(int i=1;i<=n;i++)rk2[i]=rk[i];
for(int len=1;2*len<=n;len++){
for(int i=len;i+len<=n;i+=len){
int la=min(len,askg(min(rk2[n-i+1],rk2[n-(i+len)+1])+1,max(rk2[n-i+1],rk2[n-(i+len)+1])));
int lb=min(len,askf(min(rk1[i+1],rk1[i+len+1])+1,max(rk1[i+1],rk1[i+len+1])));
int L=max(1ll,len-lb),R=min(la,len);
int l=(i+1)-R,r=(i+1)-L;
if(l<=r)a[l]++,a[r+1]--,b[l+2*len-1]++,b[r+2*len]--;
}
}
for(int i=1;i<=n;i++)a[i]+=a[i-1],b[i]+=b[i-1];
int ans=0;for(int i=1;i+1<=n;i++)ans+=b[i]*a[i+1];
printf("%lld\n",ans);
for(int i=0;i<=2*n;i++)a[i]=b[i]=rk1[i]=rk2[i]=rk[i]=ht[i]=sa[i]=tp[i]=0;
}
signed main(){
int T=read();
while(T--){
solve();
}
return 0;
}
M - 字符串
智慧放缩。
这个条件看上去就不是很好统计的样子,考虑弱化它,找一个必要条件,然后减去不合法的情况。令 \(t=s+('z'+1)+rev(s)+('a'-1)\),\(m=|t|\),注意到一个二元组 \((i,k)\) 合法的必要条件是 \(t[i\ldots m]<t[m-i+1-2k\ldots m]\),这个可以后缀数组求一下。
记 \(r_i\) 表示最大的 \(l\),满足 \(s[i-l+1\ldots i]=s[i+1\ldots i+l]\)。注意到当 \(i+k-1=j\),\([i,i+2k-1]\subset [j-r_j+1,j+r_j]\) 且 \(s_{j-r_j}<s_{j+r_j+1}\) 时这不是充分条件,这就等价于对每个询问 \((i,k)\),求 \(j-r_j+1\le i\),且 \(i\le j\le i+k-1\) 的 \(j\) 的个数,扫一遍即可。
复杂度 \(\mathcal{O}(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18;
const ull base=13331;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int rk[400015],sa[400015],c[400015],tp[400015];char s[200015],t[200015];
int cmp(int x,int y,int w){
return (tp[x]==tp[y]&&tp[x+w]==tp[y+w]);
}
void buildSA(int n){
int m='z'+1;
for(int i=1;i<=n;i++)rk[i]=t[i],tp[i]=i;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int w=1,p=0;;w<<=1){
for(int i=n;i>=n-w+1;i--)tp[++p]=i;
for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int i=1;i<=n;i++)tp[i]=rk[i];
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)rk[sa[i]]=(cmp(sa[i-1],sa[i],w)?p:++p);
if(p==n)break;
m=p,p=0;
}
}
int ht[200015];ull pw[200015],f[200015],g[200015];
ull askf(int l,int r){
return f[r]-f[l-1]*pw[r-l+1];
}
ull askg(int l,int r){
return g[l]-g[r+1]*pw[r-l+1];
}
struct BIT{
int n,c[400015];
void build(int _n){
n=_n;
for(int i=1;i<=n;i++)c[i]=0;
}
void add(int x,int v){
for(;x<=n;x+=x&-x)c[x]+=v;
}
int ask(int x){
int res=0;
for(;x;x-=x&-x)res+=c[x];
return res;
}
int ask(int l,int r){
l=max(l,1ll),r=min(r,n);
if(l>r)return 0;
return ask(r)-ask(l-1);
}
}Tr[2];
int qi[100005],qk[100005],ans[100005];vector<int>v[100005],w[100005];
void solve(){
int n=read(),m=0,q=read();scanf("%s",s+1);
for(int i=1;i<=n;i++)t[++m]=s[i];
t[++m]='z'+1;
for(int i=n;i>=1;i--)t[++m]=s[i];
t[++m]='a'-1;
buildSA(m);
for(int i=1,k=0;i<=m;i++){
if(rk[i]==1){ht[rk[i]]=0;continue;}
if(k)k--;
while(t[i+k]==t[sa[rk[i]-1]+k])k++;
ht[rk[i]]=k;
}
pw[0]=1;for(int i=1;i<=n;i++)pw[i]=pw[i-1]*base;
f[0]=0;for(int i=1;i<=n;i++)f[i]=f[i-1]*base+s[i];
g[n+1]=0;for(int i=n;i>=1;i--)g[i]=g[i+1]*base+s[i];
for(int i=1;i<=q;i++)qi[i]=read(),qk[i]=read(),v[qi[i]].push_back(i);
for(int i=1;i<=q;i++)qk[i]=min(qk[i],(n+1-qi[i])/2);
for(int i=0;i<2;i++)Tr[i].build(m);
for(int i=m;i>=1;i--){
if(sa[i]<=n){
for(auto x:v[sa[i]]){
ans[x]=Tr[(sa[i]+1)&1ll].ask(m-sa[i]+1-2*qk[x],m-sa[i]+1-2);
}
}
Tr[sa[i]&1ll].add(sa[i],1);
}
for(int i=1;i<=n;i++){
int l=1,r=min(i,n-i),res=0;
while(l<=r){
int mid=(l+r)>>1;
if(askf(i-mid+1,i)==askg(i+1,i+mid))res=mid,l=mid+1;
else r=mid-1;
}
if(!res||i-res+1==1||i+res==n||s[i-res]<s[i+res+1])continue;
w[i-res+1].push_back(i);
}
Tr[0].build(m);
for(int i=1;i<=n;i++){
for(auto x:w[i])Tr[0].add(x,1);
for(auto x:v[i])ans[x]-=Tr[0].ask(qi[x],qi[x]+qk[x]-1);
}
for(int i=1;i<=q;i++)printf("%lld\n",ans[i]);
for(int i=0;i<=2*m;i++)sa[i]=rk[i]=tp[i]=c[i]=0;
for(int i=0;i<=n;i++)s[i]=0,v[i].clear(),w[i].clear();
for(int i=0;i<=m;i++)t[i]=ht[i]=0;
}
signed main(){
int C=read(),T=read();
while(T--){
solve();
}
return 0;
}
N - 事情的相似度
这是一个 SA + 回滚莫队 + 分块的 \(n\sqrt{n}\) 做法。
把整个串 reverse 一下,问题就是结束点在 \([l,r]\) 范围内的任意两个后缀的 lcp 的 max。不难发现 max 只会在区间内排名相邻的两个后缀处取到。考虑只删的回滚莫队,链表维护前驱后继。考虑怎么统计答案。注意到修改次数为 \(\mathcal{O}(n\sqrt{n})\) 而只会询问 \(\mathcal{O}(n)\) 次,且答案不超过 \(n\)。考虑把所有备选答案丢到值域分块上,复杂度 \(\mathcal{O}(n\log n+n\sqrt{n})\)。
SAM 做法学会了 lct 再补。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int n,Q,siz,num,rk[1000005],c[1000005],sa[1000005],tp[1000005],ht[1000005];char s[1000005];
int cmp(int x,int y,int w){
return (tp[x]==tp[y]&&tp[x+w]==tp[y+w]);
}
void buildSA(){
int m='1';
for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int w=1,p=0;;w<<=1){
for(int i=n;i>=n-w+1;i--)tp[++p]=i;
for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int i=1;i<=n;i++)tp[i]=rk[i];
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)rk[sa[i]]=(cmp(sa[i-1],sa[i],w)?p:++p);
if(p==n)break;
m=p,p=0;
}
}
struct Que{
int l,r,id;
}q[100005];
int bel[100005],L[505],R[505];
int Cmp(Que x,Que y){
if(bel[x.l]!=bel[y.l])return bel[x.l]<bel[y.l];
else return x.r>y.r;
}
int f[20][100005];
int ask(int l,int r){
assert(l<=r);
if(l>r)return inf;
int o=__lg(r-l+1);
return min(f[o][l],f[o][r-(1ll<<o)+1]);
}
int B[100005],cnt[100005],pre[100005],nxt[100005],s1[100005],s2[505],ans[100005];
void Add(int x,int v){
s1[x]+=v,s2[bel[x]]+=v;
}
int Ask(){
for(int i=num;i>=1;i--){
if(s2[i]){
for(int j=R[i];j>=L[i];j--)if(s1[j])return j;
return 0;
}
}
return 0;
}
void del(int x){
if(pre[x])Add(ask(pre[x]+1,x),-1);
if(nxt[x])Add(ask(x+1,nxt[x]),-1);
if(pre[x]&&nxt[x])Add(ask(pre[x]+1,nxt[x]),1);
pre[nxt[x]]=pre[x],nxt[pre[x]]=nxt[x];
}
struct Node{
int a,b,c;
};
signed main(){
n=read(),Q=read(),siz=(int)sqrt(n),num=(n+siz-1)/siz;
for(int i=1;i<=n;i++)bel[i]=(i-1)/siz+1;
for(int i=1;i<=num;i++)L[i]=(i-1)*siz+1,R[i]=min(n,i*siz);
scanf("%s",s+1);reverse(s+1,s+n+1);buildSA();
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1){ht[rk[i]]=0;continue;}
if(k)k--;
while(s[i+k]==s[sa[rk[i]-1]+k])k++;
ht[rk[i]]=k;
}
for(int i=1;i<=n;i++)f[0][i]=ht[i];
for(int j=1;(1ll<<j)<=n;j++){
for(int i=1;i+(1ll<<j)-1<=n;i++){
f[j][i]=min(f[j-1][i],f[j-1][i+(1ll<<(j-1))]);
}
}
for(int i=1,l,r;i<=Q;i++){
l=read(),r=read(),q[i]=(Que){n-r+1,n-l+1,i};
}
sort(q+1,q+Q+1,Cmp);
for(int j=1,i=1;j<=num;j++){
int l=L[j],r=n,lst=0;
for(int k=0;k<=n;k++)B[k]=cnt[k]=pre[k]=nxt[k]=0;
for(int k=1;k<=n;k++)s1[k]=0;
for(int k=1;k<=num;k++)s2[k]=0;
for(int k=L[j];k<=n;k++)cnt[rk[k]]++;
for(int k=1;k<=n;k++)if(cnt[k])pre[k]=lst,nxt[lst]=k,lst=k;
for(int k=1;k<=n;k++)if(cnt[k]&&pre[k])Add(ask(pre[k]+1,k),1);
while(i<=Q){
int ql=q[i].l,qr=q[i].r,id=q[i].id;
if(bel[ql]!=j)break;
while(r>qr)del(rk[r--]);
stack<Node>s;
while(l<ql)s.push((Node){rk[l],pre[rk[l]],nxt[rk[l]]}),del(rk[l++]);
ans[id]=Ask();
l=L[j];
while(!s.empty()){
Node u=s.top();s.pop();
if(u.b&&u.c)Add(ask(u.b+1,u.c),-1);
if(u.b)Add(ask(u.b+1,u.a),1);
if(u.c)Add(ask(u.a+1,u.c),1);
nxt[u.b]=u.a,pre[u.a]=u.b,pre[u.c]=u.a,nxt[u.a]=u.c;
}
i++;
}
}
for(int i=1;i<=Q;i++)printf("%lld\n",ans[i]);
return 0;
}
O - Simple KMP
考虑把贡献写得形式化一点。
不妨记一个 \(f(i)=\sum\limits_{l=1}^i\sum\limits_{k=1}^{i-l}[s[l\ldots l+k-1]=s[i-k+1\ldots i]]\)。那么 \(key(s)=\sum\limits_{r=1}^n\sum\limits_{i=1}^r f(i)\)。考虑求 \(f(i)\)。当然我们不可能在线做。考虑对整个 \(s\) 建 sam,枚举 \(i=1\sim n\),记 \(s[1\ldots i]\) 在 parent 树上对应的点为 \(x_i\),只需要对 \(x_i\) 到 \(1\) 路径 \(cnt\) 加一,\(x_i\) 到根求和,即可得到 \(f(i)\),对 \(f(i)\) 做两遍前缀和就是答案。大力树剖即可维护,复杂度 \(\mathcal{O}(n\log^2 n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18,mod=1e9+7;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct SAM{
int tot=1,lst=1,ch[200005][28],link[200005],len[200005];
vector<int>g[200005];
void add(int c){
int y=lst,x=++tot;lst=x,len[x]=len[y]+1;
while(y&&!ch[y][c])ch[y][c]=x,y=link[y];
if(!y){link[x]=1;return;}
int p=y,q=ch[p][c];
if(len[q]==len[p]+1){link[x]=q;return;}
int Q=++tot;len[Q]=len[p]+1;
link[Q]=link[q],link[q]=link[x]=Q;
for(int i=0;i<26;i++)ch[Q][i]=ch[q][i];
while(y&&ch[y][c]==q)ch[y][c]=Q,y=link[y];
}
void build(){
for(int i=2;i<=tot;i++)g[link[i]].push_back(i);
}
}sam;
int s[200005];
struct segtree{
#define ls p<<1
#define rs p<<1|1
#define lson l,mid,ls
#define rson mid+1,r,rs
struct Node{
int s,tag;
}c[800005];
void pushup(int p){
c[p].s=(c[ls].s+c[rs].s)%mod;
}
void pushdown(int l,int r,int p){
if(!c[p].tag)return;
int mid=(l+r)>>1;
c[ls].s=(c[ls].s+(s[mid]-s[l-1]+mod)%mod*c[p].tag%mod)%mod;
c[rs].s=(c[rs].s+(s[r]-s[mid]+mod)%mod*c[p].tag%mod)%mod;
c[ls].tag=(c[ls].tag+c[p].tag)%mod,c[rs].tag=(c[rs].tag+c[p].tag)%mod;
c[p].tag=0;
}
void build(int l,int r,int p){
c[p].tag=0;
if(l==r){c[p].s=0;return;}
int mid=(l+r)>>1;
build(lson),build(rson);
pushup(p);
}
void add(int l,int r,int p,int L,int R,int k){
if(L<=l&&r<=R){c[p].s=(c[p].s+(s[r]-s[l-1]+mod)%mod*k%mod)%mod,c[p].tag=(c[p].tag+k)%mod;return;}
int mid=(l+r)>>1;pushdown(l,r,p);
if(L<=mid)add(lson,L,R,k);
if(R>mid)add(rson,L,R,k);
pushup(p);
}
int qry(int l,int r,int p,int L,int R){
if(L<=l&&r<=R)return c[p].s;
int mid=(l+r)>>1,res=0;pushdown(l,r,p);
if(L<=mid)res=(res+qry(lson,L,R))%mod;
if(R>mid)res=(res+qry(rson,L,R))%mod;
return res;
}
#undef ls
#undef rs
#undef lson
#undef rson
}Tr;
int siz[200005],son[200005],dep[200005];
void dfs1(int u){
siz[u]=1,son[u]=0;
for(auto v:sam.g[u]){
dep[v]=dep[u]+1,dfs1(v),siz[u]+=siz[v];
if(siz[son[u]]<siz[v])son[u]=v;
}
}
int cur,dfn[200005],rnk[200005],top[200005];
void dfs2(int u,int rt){
dfn[u]=++cur,rnk[cur]=u,top[u]=rt;
if(son[u])dfs2(son[u],rt);
for(auto v:sam.g[u]){
if(v!=son[u])dfs2(v,v);
}
}
void addPath(int u,int v,int k){
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);
Tr.add(1,cur,1,dfn[top[u]],dfn[u],k);
u=sam.link[top[u]];
}
if(dep[u]<dep[v])swap(u,v);
Tr.add(1,cur,1,dfn[v],dfn[u],k);
}
int askPath(int u,int v){
int res=0;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);
res=(res+Tr.qry(1,cur,1,dfn[top[u]],dfn[u]))%mod;
u=sam.link[top[u]];
}
if(dep[u]<dep[v])swap(u,v);
res=(res+Tr.qry(1,cur,1,dfn[v],dfn[u]))%mod;
return res;
}
int ans[100005];char t[100005];
signed main(){
int n=read();scanf("%s",t+1);
for(int i=1;i<=n;i++)sam.add(t[i]-'a');
sam.build();dfs1(1);dfs2(1,1);
for(int i=1;i<=cur;i++)s[i]=(s[i-1]+sam.len[rnk[i]]-sam.len[sam.link[rnk[i]]])%mod;
Tr.build(1,cur,1);
for(int i=1,u=1;i<=n;i++){
u=sam.ch[u][t[i]-'a'];ans[i]=(ans[i-1]+askPath(u,1))%mod;addPath(u,1,1);
}
for(int i=1;i<=n;i++)ans[i]=(ans[i]+ans[i-1])%mod;
for(int i=1;i<=n;i++)printf("%lld\n",ans[i]);
return 0;
}
P - Substrings in a String
一个 bitset 做法。
考虑优化暴力匹配的过程。对文本串 \(s\) 中每种字符开一个 bitset \(B_c\) 表示字符 c 的所有出现位置。对于求文本串 \(t\) 在 \([l,r]\) 中每次出现的出现位置,定义 \(len\) 为 \(t\) 的长度,我们有以下套路:定义 bitset \(X\),\(X\) 中第 \(i\) 位为 1 表示 \([i,i+len-1]\) 为 \(t\)。遍历 \(t\) 的每一位,同时 \(X\leftarrow X\And B_{t_i}\),最后 \(X\) 中为 1 的位置即为所求。本题中我们统计的是 \(X\) 中 \([l,r-len+1]\) 的答案。注意特判 \(len>r-l+1\) 的情况。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int id(char ch){
if('a'<=ch&&ch<='z')return ch-'a';
if('A'<=ch&&ch<='Z')return ch-'A'+26;
if('0'<=ch&&ch<='9')return ch-'0'+52;
return ch-'_'+62;
}
char s[100005],t[100005];bitset<100005>B[64],ans;
int ask(bitset<100005>a,int l,int r,int len){
return (a>>l).count()-(a>>(r-len+2)).count();
}
signed main(){
scanf("%s",s+1);int n=strlen(s+1),m=read();for(int i=1;i<=n;i++)B[id(s[i])].flip(i);
while(m--){
int op=read(),l,r;
if(op==1){l=r=read();scanf("%s",t+1);for(int i=l;i<=r;i++)B[id(s[i])].flip(i),s[i]=t[i-l+1],B[id(s[i])].flip(i);}
else{l=read(),r=read();scanf("%s",t+1);int len=strlen(t+1);if(len>r-l+1){puts("0");continue;}ans.set();for(int i=1;i<=len;i++)ans&=(B[id(t[i])]>>(i-1));printf("%d\n",ask(ans,l,r,len));}
}
return 0;
}
一个正经的分块 sam 做法。下文假定 \(|s|=n\),\(q\),\(\sum|y|\) 同阶。
考虑每次询问直接 kmp 暴力匹配,复杂度 \(\mathcal{O}(n^2)\)。注意到这样很慢的原因在于 kmp 匹配的复杂度是 \(\mathcal{O}(n+m)\),考虑一些能统计出现次数,且复杂度与 \(n\) 无关的东西,比如 sam。注意到还需要维护修改操作,还有这个 \(10^5\) 的看起来就很根号的数据范围,考虑分块,对每个长为 \(T\) 的块建一个 sam,每次修改时暴力重构。复杂度 \(\mathcal{O}(nT)\)。
思考现在怎么匹配。对于 \(|y|>T\),这样的询问只会出现不超过 \(\dfrac{\sum|y|}{T}\) 次,可以直接暴力建 sam 然后匹配,复杂度 \(\mathcal{O}(\dfrac{n^2}{T})\)。否则 \(y\) 要么在一个块里,要么在两个块中间,在块里可以直接用维护的 sam 匹配,边角块可以暴力建 sam,复杂度 \(\mathcal{O}(\dfrac{n^2}{T}+nT)\)。另一种情况可以枚举 \(y\) 在哪两个块中间,算出可能的范围后建 sam。注意到这个区间长度不超过 \(2|y|\),复杂度 \(\mathcal{O}(\dfrac{n^2}{T})\)。
取 \(T=\sqrt{n}\) 可以得到复杂度 \(\mathcal{O}(n\sqrt{n})\)。看上去很快?实际上因为建 sam 的复杂度是 \(\mathcal{O}(|\sum|n)\) 而不是 \(\mathcal{O}(n)\),还需要带一个 26 的常数,需要大力卡常。比如刚刚那些暴力建 sam 的地方可以用 kmp 少掉一个 26 的常数,只有块内需要用 sam。如果还不能过的话可以调下块长。重构记得清空 parent 树,不然会 mle。
跑得很慢,被 bitset 做法爆踩。
点击查看代码
#include<bits/stdc++.h>
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct SAM{
int tot=1,lst=1,ch[705][28],link[705],len[705],siz[705];vector<int>g[705];
void clear(){
for(int i=1;i<=tot;i++){
for(int j=0;j<26;j++)ch[i][j]=0;
link[i]=len[i]=siz[i]=0;
vector<int>().swap(g[i]);
}
tot=lst=1;
}
void add(int c){
int y=lst,x=++tot;lst=x;len[x]=len[y]+1,siz[x]=1;
while(y&&!ch[y][c])ch[y][c]=x,y=link[y];
if(!y){link[x]=1;return;}
int p=y,q=ch[p][c];
if(len[q]==len[p]+1){link[x]=q;return;}
int Q=++tot;link[Q]=link[q],link[q]=link[x]=Q;len[Q]=len[p]+1;
for(int i=0;i<26;i++)ch[Q][i]=ch[q][i];
while(y&&ch[y][c]==q)ch[y][c]=Q,y=link[y];
}
void build(){
for(int i=2;i<=tot;i++)g[link[i]].push_back(i);
}
void dfs(int u){
for(auto v:g[u])dfs(v),siz[u]+=siz[v];
}
int calc(char *t,int len){
int u=1;
for(int i=1;i<=len;i++){
if(!ch[u][t[i]-'a'])return 0;
u=ch[u][t[i]-'a'];
}
return siz[u];
}
}sam[355];
int bel[100005],L[355],R[355],nxt[100005];char s[100005],t[100005];
void initnxt(int len){
nxt[1]=0;
for(int i=2,j=0;i<=len;i++){
while(j&&t[j+1]!=t[i])j=nxt[j];
if(t[j+1]==t[i])j++;
nxt[i]=j;
}
}
int count(int l,int r,int len){
int ans=0;
for(int i=l,j=0;i<=r;i++){
while(j&&t[j+1]!=s[i])j=nxt[j];
if(t[j+1]==s[i])j++;
if(j==len)ans++,j=nxt[j];
}
return ans;
}
signed main(){
scanf("%s",s+1);
int n=strlen(s+1),siz=(int)sqrt(n),num=(n+siz-1)/siz;
for(int i=1;i<=n;i++)bel[i]=(i-1)/siz+1;
for(int i=1;i<=num;i++)L[i]=(i-1)*siz+1,R[i]=min(i*siz,n);
for(int i=1;i<=num;i++){
sam[i].clear();
for(int j=L[i];j<=R[i];j++)sam[i].add(s[j]-'a');
sam[i].build();sam[i].dfs(1);
}
int q=read();
while(q--){
int op=read();
if(op==1){
int i=read();scanf("%s",t+1);s[i]=t[1];
i=bel[i];sam[i].clear();
for(int j=L[i];j<=R[i];j++)sam[i].add(s[j]-'a');
sam[i].build();sam[i].dfs(1);
}
else{
int l=read(),r=read();scanf("%s",t+1);
int len=strlen(t+1),ans=0;
if(len>r-l+1){puts("0");continue;}
initnxt(len);
if(len<=siz){
if(bel[l]==bel[r])ans+=count(l,r,len);
else{
ans+=count(l,R[bel[l]],len);
ans+=count(L[bel[r]],r,len);
for(int i=bel[l]+1;i<=bel[r]-1;i++){
if(R[i]-L[i]+1<len)continue;
ans+=sam[i].calc(t,len);
}
for(int i=bel[l];i<=bel[r]-1;i++){
int lp=max(1,len-r-1+L[i+1]),rp=min(len-1,R[i]+1-l);
if(lp<=rp)ans+=count(R[i]+1-rp,(R[i]+1-lp)+len-1,len);
}
}
}
else ans+=count(l,r,len);
printf("%d\n",ans);
}
}
return 0;
}
R - 封印
一个 SA 做法!
考虑把 \(t\) 拼到 \(s\) 后面,中间随便插一个什么别的字符。先对这个串跑个 SA,假设当前是问 \([l,r]\),考虑二分答案 mid,需要判定 \(\max\text{lcp}(s[i\ldots |s|+|t|+1],s[j+|s|+1\ldots |s|+|t|+1])\) 是否 \(\ge mid\),其中 \(i\in[i,r-mid+1]\),\(j\in[|s|+2,|s|+|t|+2-mid]\)。注意到 \(j\) 的范围限制是没意义的,可以直接取满 \(t\) 对应的范围。然后因为 \(j\) 的范围已经可以取满了,需要求 \(\max \text{lcp}\),那么一个 \(i\) 一定是和它左右两边最近的 \(j\) 匹配,可以 ST 表预处理,复杂度 \(\mathcal{O}(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int n,m,sa[8000005],rk[8000005],c[4000005],tp[8000005],ht[4000005];char s[4000005],t[2000005];
int cmp(int x,int y,int w){
return (tp[x]==tp[y]&&tp[x+w]==tp[y+w]);
}
void buildSA(){
m=max('z','#');
for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=0;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int w=1,p=0;;w<<=1){
for(int i=1;i<=w;i++)tp[++p]=n-w+i;
for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
for(int i=0;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[rk[i]]++;
for(int i=0;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[rk[tp[i]]]--]=tp[i];
for(int i=1;i<=n;i++)tp[i]=rk[i];
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)rk[sa[i]]=(cmp(sa[i-1],sa[i],w)?p:++p);
if(p==n)break;
m=p,p=0;
}
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1){ht[rk[i]]=0;continue;}
if(k)--k;
int j=sa[rk[i]-1];
while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k])k++;
ht[rk[i]]=k;
}
}
int Log[8000005],f[2000005][25],g[4000005][25];
int askF(int l,int r){
int o=Log[r-l+1];
return max(f[l][o],f[r-(1ll<<o)+1][o]);
}
int askG(int l,int r){
int o=Log[r-l+1];
return min(g[l][o],g[r-(1ll<<o)+1][o]);
}
signed main(){
scanf("%s%s",s+1,t+1);
int N=strlen(s+1),M=strlen(t+1);
s[++N]='#',n=N;
for(int i=1;i<=M;i++)s[i+n]=t[i];
n+=M;buildSA();
Log[1]=0;
for(int i=2;i<=N;i++)Log[i]=Log[i>>1]+1;
for(int i=1;i<=N+M;i++)g[i][0]=ht[i];
for(int j=1;(1ll<<j)<=N+M;j++){
for(int i=1;i+(1ll<<j)-1<=N+M;i++){
g[i][j]=min(g[i][j-1],g[i+(1ll<<(j-1))][j-1]);
}
}
int lst=0;
for(int i=1;i<=N;i++)f[i][0]=-inf;
for(int i=1;i<=N+M;i++){
if(sa[i]>N)lst=i;
else if(lst)f[sa[i]][0]=max(f[sa[i]][0],askG(lst+1,i));
}
lst=0;
for(int i=N+M;i>=1;i--){
if(sa[i]>N)lst=i;
else if(lst)f[sa[i]][0]=max(f[sa[i]][0],askG(i+1,lst));
}
for(int j=1;(1ll<<j)<=N;j++){
for(int i=1;i+(1ll<<j)-1<=N;i++){
f[i][j]=max(f[i][j-1],f[i+(1ll<<(j-1))][j-1]);
}
}
int q=read();
while(q--){
int L=read(),R=read();
int l=0,r=R-L+1,res=0;
while(l<=r){
int mid=(l+r)>>1;
if(askF(L,R-mid+1)>=mid)res=mid,l=mid+1;
else r=mid-1;
}
printf("%lld\n",res);
}
return 0;
}
一个 sam 做法。
求 \(s[l\ldots r]\) 和 \(t\) 的最长公共子串,不妨二分答案 \(L\),即求 \(\exists i\in[l,r-L+1]\),\(s[1\ldots i]\) 和 \(t\) 的最长公共子串长度 \(\ge L\)。
套路的,考虑对 \(t\) 建 sam,预处理 \(s\) 的每个前缀与 \(t\) 的最长公共子串的长度。考虑从小到大处理。对于 \(s[1\ldots i]\),这就相当于在 sam 上找一条最长的路径,满足它是这个前缀的一段后缀。记处理到 \(i-1\) 后的当前节点为 \(u\) 和当前答案为 \(t\),如果 \(trans(u,s_i)\) 存在那么直接 \(u\gets trans(u,s_i)\),\(t\gets t+1\)。否则,我们需要不断截取一段后缀,即 \(u\gets link(u)\),\(t\gets len(u)\),直到它存在转移。
注意此时不能简单的令答案为 \(len(u)\),因为我们只知道答案在 \(u\) 这个节点对应的字符串集合里,所以 \(len(u)\) 不一定是答案。但是在跳 \(link\) 时答案一定就是 \(len\) 了。
复杂度显然 \(\mathcal{O}(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define fi first
#define se second
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
typedef pair<int,int>pii;
const int inf=1e18;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct SAM{
int tot=1,lst=1,ch[400005][28],link[400005],len[400005];
void add(int c){
int y=lst,x=++tot;lst=x;len[x]=len[y]+1;
while(y&&!ch[y][c])ch[y][c]=x,y=link[y];
if(!y){link[x]=1;return;}
int p=y,q=ch[p][c];
if(len[q]==len[p]+1){link[x]=q;return;}
int Q=++tot;len[Q]=len[p]+1;
link[Q]=link[q],link[q]=link[x]=Q;
for(int i=0;i<26;i++)ch[Q][i]=ch[q][i];
while(y&&ch[y][c]==q)ch[y][c]=Q,y=link[y];
}
}sam;
int f[20][200005];
int ask(int l,int r){
assert(l<=r);
int o=__lg(r-l+1);
return max(f[o][l],f[o][r-(1ll<<o)+1]);
}
char s[200005],t[200005];
signed main(){
scanf("%s%s",s+1,t+1);
int n=strlen(s+1),m=strlen(t+1),q=read();
for(int i=1;i<=m;i++)sam.add(t[i]-'a');
for(int i=1,u=1,l=0;i<=n;i++){
while(u&&!sam.ch[u][s[i]-'a'])u=sam.link[u],l=sam.len[u];
if(u)u=sam.ch[u][s[i]-'a'],l++;
else u=1,l=0;
f[0][i]=l;
}
for(int j=1;(1ll<<j)<=n;j++){
for(int i=1;i+(1ll<<j)-1<=n;i++){
f[j][i]=max(f[j-1][i],f[j-1][i+(1ll<<(j-1))]);
}
}
while(q--){
int a=read(),b=read();
int l=1,r=b-a+1,res=0;
while(l<=r){
int mid=(l+r)>>1;
if(ask(a+mid-1,b)>=mid)res=mid,l=mid+1;
else r=mid-1;
}
printf("%lld\n",res);
}
return 0;
}
Q - 匹配
我什么时候写过这种东西???
点击查看代码
#include<bits/stdc++.h>
#define int long long
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e18,V=1e9;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct SAM{
int tot=1,lst=1,ch[200005][12],link[200005],len[200005];
vector<int>g[200005];
void clear(){
for(int i=1;i<=tot;i++){
link[i]=len[i]=0,g[i].clear();
for(int j=0;j<10;j++)ch[i][j]=0;
g[i].shrink_to_fit();
}
tot=lst=1;
}
void add(int c){
int y=lst,x=++tot;lst=x,len[x]=len[y]+1;
while(y&&!ch[y][c])ch[y][c]=x,y=link[y];
if(!y){link[x]=1;return;}
int p=y,q=ch[p][c];
if(len[q]==len[p]+1){link[x]=q;return;}
int Q=++tot;len[Q]=len[p]+1;
link[Q]=link[q],link[q]=link[x]=Q;
for(int i=0;i<10;i++)ch[Q][i]=ch[q][i];
while(y&&ch[y][c]==q)ch[y][c]=Q,y=link[y];
}
void build(){
for(int i=2;i<=tot;i++)g[link[i]].push_back(i);
}
}sam;
int pos[200005];
void dfs1(int u){
for(auto v:sam.g[u]){
dfs1(v);pos[u]=min(pos[u],pos[v]);
}
}
int cur,siz[200005],dfn[200005];
void dfs2(int u){
siz[u]=1,dfn[u]=++cur;
for(auto v:sam.g[u]){
dfs2(v);siz[u]+=siz[v];
}
}
struct BIT{
int c[200005];
void add(int x,int v){
for(;x<=cur;x+=x&-x)c[x]+=v;
}
int ask(int x){
int res=0;
for(;x;x-=x&-x)res+=c[x];
return res;
}
int ask(int l,int r){
return ask(r)-ask(l-1);
}
}Tr;
int ans[50005];char s[100005];string t[50005];vector<pair<int,int> >q[100005];
signed main(){
int n=read();scanf("%s",s+1);
for(int i=1;i<=n;i++)sam.add(s[i]-'0');
int m=read();sam.build();
for(int i=1;i<=sam.tot;i++)pos[i]=inf;
for(int i=1,u=1;i<=n;i++){
u=sam.ch[u][s[i]-'0'],pos[u]=min(pos[u],i);
}
dfs1(1);dfs2(1);
for(int i=1;i<=m;i++){
cin>>t[i];int len=(int)t[i].size(),u=1;
for(int j=0;j<len;j++){
u=sam.ch[u][t[i][j]-'0'];
if(!u)break;
}
if(!u){
for(int j=0,v=1;j<len;j++){
v=sam.ch[v][t[i][j]-'0'];
if(!v)break;
q[n+1].push_back({i,v});
}
ans[i]+=n;
}
else{
assert(pos[u]<=n);
for(int j=0,v=1;j<len;j++){
v=sam.ch[v][t[i][j]-'0'];
q[pos[u]-len+1+j].push_back({i,v});
}
ans[i]+=pos[u];
}
}
for(int i=1,u=1;i<=n+1;i++){
for(auto x:q[i]){
ans[x.first]+=Tr.ask(dfn[x.second],dfn[x.second]+siz[x.second]-1);
// msg("{%lld,%lld,%lld}{%lld}\n",i,x.first,x.second,Tr.ask(dfn[x.second],dfn[x.second]+siz[x.second]-1));
}
if(i<=n)u=sam.ch[u][s[i]-'0'],Tr.add(dfn[u],1);
}
for(int i=1;i<=m;i++)printf("%lld\n",ans[i]);
return 0;
}
/*
7
1090901
1
0901
*/
U - Palindrome Addicts
坏了,以前没写题解吗,补一下。
点击查看代码
#include<bits/stdc++.h>
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
const int inf=1e9;
inline int read(){
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int l=1,r=0;char s[1000005];
struct PAM{
//odd->1 even->0
int lst=0,tot=1,num=0,ch[2000005][28],fail[2000005],len[2000005],tag[2000005],g[2000005];
vector<int>t[2000005];
void clear(){
for(int i=0;i<=tot;i++){
fail[i]=len[i]=tag[i]=g[i]=0;
for(int j=0;j<26;j++)ch[i][j]=0;
}
lst=0,tot=1,num=0,fail[0]=1,fail[1]=1,len[0]=0,len[1]=-1;
}
void upd(int p,int k){
if(p<2||!k)return;
if(tag[p]==0)num++,g[fail[p]]++;
if(tag[p]<k)tag[p]=k,t[k-len[p]+1].push_back(p);
}
int getfail(int x,int i){
while(i-len[x]-1<0||s[i-len[x]-1]!=s[i]){
msg("{%d,%d}{%d,%d}\n",x,i,fail[x],tag[x]),upd(fail[x],tag[x]),x=fail[x];
}
return x;
}
void add(int i){
int p=getfail(lst,i);
if(!ch[p][s[i]-'a']){
int q=++tot;len[q]=len[p]+2;
fail[q]=ch[getfail(fail[p],i)][s[i]-'a'],ch[p][s[i]-'a']=q;
}
lst=ch[p][s[i]-'a'];
while(len[lst]>r-l+1)lst=fail[lst];
upd(lst,i);
}
void del(int i){
for(int j=0;j<(int)t[i].size();j++){
int x=t[i][j];
if(!g[x]&&tag[x]-len[x]+1==i)num--,g[fail[x]]--,upd(fail[x],tag[x]),tag[x]=0;
}
}
}pam;
char op[15];
signed main(){
int q=read();pam.clear();
while(q--){
scanf("%s",op);
if(op[1]=='u')scanf("%s",op),s[++r]=op[0],pam.add(r);
else pam.del(l),l++;
printf("%d\n",pam.num);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号