CF794F. Leha and security system

比较水的 *2800，但是考察对标记的理解。

有一个比较原始的思路：因为需要让所有数码为 \(x\) 的改成 \(y\)，我们不难想到这样一个做法：对十进制下第 \(1,2,3\ldots 10\) 位各开一棵线段树，每个节点存区间内每种数码的出现次数 \(cnt_i\)，最后用位值原理合并得到答案。

对于区间修改操作，我们打标记 \(tag_i\) 表示初始为 \(i\) 的数码会改成什么。在将当前点的标记下传给左右儿子的过程中，我们要将儿子的标记和父亲的合并，而这就是我们要讲的重点：

首先，父亲的标记对应的修改的操作时间，一定在儿子的标记之后。因为如果在儿子之前，肯定已经在儿子当前的标记下传到儿子的同时已经处理了；然后，对于让人头晕的具体如何合并的问题，我们可以把这个修改关系看成一张类似拓扑图的东西，就像这样：

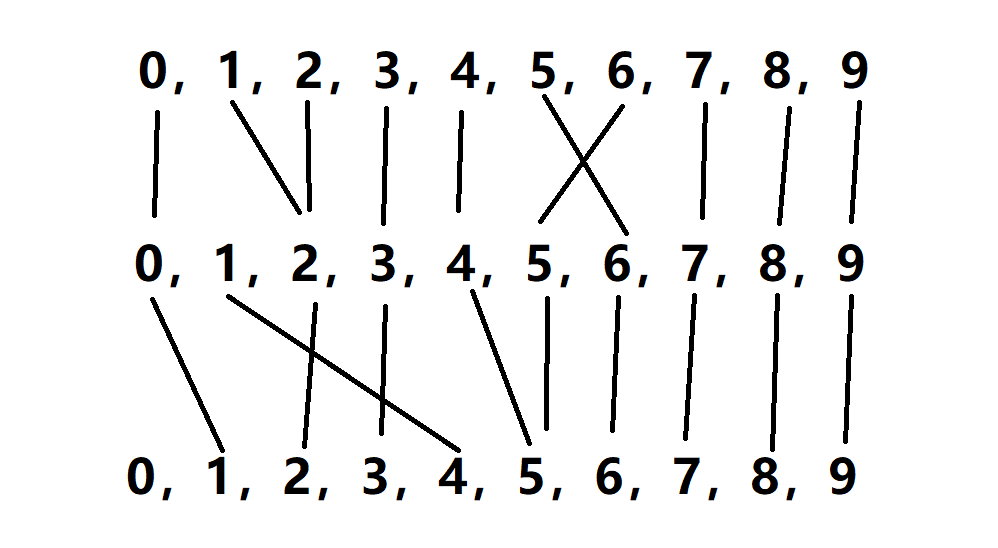
画成图再理解就清晰了很多。

但是这样是 \(O(x\cdot \log_{10}a\cdot n\log n)\) 的，也就是 \(O(n\log n)\) 带 100 的常数。常数太大过不了，怎么办？发现我们其实并不需要真的按十进制位维护答案，只需要在建树的时候把每一位取出来，\(cnt_i\) 直接维护所有数码为 \(i\) 的位置的贡献和（\(\sum\limits_{t=1}^{10}\) 十进制下从低到高第 \(t\) 位等于 \(i\) 的个数 \(\times 10^{t-1}\)）即可。时间复杂度 \(O(x\cdot n\log n)\)。

有一点细节：取出一位的时候需要避免把前导零也算进数码里。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int read(){
	int x=0,f=1;char ch=getchar();
	while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
	while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
ll pw[15],CNT[15];int a[100005],TAG[15];
struct segtree{
	struct Node{
		ll cnt[15];int tag[15];
	}c[400005];
	ll get(int p){
		ll res=0;
		for(int o=0;o<=9;++o)res+=1ll*c[p].cnt[o]*o;
		return res;
	}
	void pushup(int p){
		for(int o=0;o<=9;++o)c[p].cnt[o]=c[p<<1].cnt[o]+c[p<<1|1].cnt[o];
	}
	void pushdown(int l,int r,int p){
		for(int o=0;o<=9;++o)CNT[o]=c[p<<1].cnt[o],TAG[o]=c[p<<1].tag[o],c[p<<1].cnt[o]=0;
		for(int o=0;o<=9;++o)c[p<<1].cnt[c[p].tag[o]]+=CNT[o],c[p<<1].tag[o]=c[p].tag[TAG[o]],CNT[o]=0,TAG[o]=0;
		for(int o=0;o<=9;++o)CNT[o]=c[p<<1|1].cnt[o],TAG[o]=c[p<<1|1].tag[o],c[p<<1|1].cnt[o]=0;
		for(int o=0;o<=9;++o)c[p<<1|1].cnt[c[p].tag[o]]+=CNT[o],c[p<<1|1].tag[o]=c[p].tag[TAG[o]],CNT[o]=0,TAG[o]=0;
		for(int o=0;o<=9;++o)c[p].tag[o]=o;
	}
	void build(int l,int r,int p){
		for(int o=0;o<=9;++o)c[p].tag[o]=o;
		if(l==r){
			for(int o=0;o<=9;++o)c[p].cnt[o]=0;
			for(int k=0;k<=9;k++)if(a[l]>=pw[k])c[p].cnt[(a[l]%pw[k+1])/pw[k]]+=pw[k];
			return;
		}
		int mid=(l+r)>>1;
		build(l,mid,p<<1),build(mid+1,r,p<<1|1);
		pushup(p);
	}
	void update(int l,int r,int p,int L,int R,int x,int y){
		if(L<=l&&r<=R){
			c[p].cnt[y]+=c[p].cnt[x],c[p].cnt[x]=0ll;
			for(int o=0;o<=9;++o)if(c[p].tag[o]==x)c[p].tag[o]=y;
			return;
		}
		int mid=(l+r)>>1;pushdown(l,r,p);
		if(L<=mid)update(l,mid,p<<1,L,R,x,y);
		if(R>mid)update(mid+1,r,p<<1|1,L,R,x,y);
		pushup(p);
	}
	ll query(int l,int r,int p,int L,int R){
		if(L<=l&&r<=R)return get(p);
		int mid=(l+r)>>1;ll res=0ll;pushdown(l,r,p);
		if(L<=mid)res+=query(l,mid,p<<1,L,R);
		if(R>mid)res+=query(mid+1,r,p<<1|1,L,R);
		return res;
	}
}Tr;
signed main(){
	pw[0]=1ll;
	for(int o=1;o<=10;++o)pw[o]=10ll*pw[o-1];
	int n=read(),k=read();
	for(int i=1;i<=n;++i)a[i]=read();
	Tr.build(1,n,1);
	while(k--){
		int op=read();
		if(op==1){
			int l=read(),r=read(),x=read(),y=read();
			if(x==y)continue;
			Tr.update(1,n,1,l,r,x,y);
		}
		else{
			int l=read(),r=read();
			printf("%lld\n",Tr.query(1,n,1,l,r));
		}
	}
	return 0;
}