4月AT杂题

AtCoder Beginner Contest 296

D - M<=ab

题意：求最小的正整数，不小于 \(m\)，且能被表示为两个不大于 \(n\) 的正整数的数，不存在输出 -1。\(n,m\le10^{12}\)。

直接枚举 \(a\)，计算最小的满足 \(ab\ge m\) 的 \(b\)，如果 \(a>b\) 则后面的情况一定是重复的。时间复杂度 \(\text{O}(\sqrt m)\)。最好用 __int128 。

E - Transition Game

题意：给一个 \(n\) 个点 \(n\) 条形如 \(i\rightarrow a_i\) 的有向边的图，求有多少个点在环中（包括自环）。\(n,a_i\le2\times10^5\)。

\(\text{tarjan}\) 缩点或者拓扑找环即可。

F - Simultaneous Swap

题意：给你两个数组 \(a,b\)。可以进行任意次如下操作，问最后是否能使 \(a,b\) 数组相等：选择互不相等的 \(i,j,k\)，交换 \(a_i,a_j\) 和 \(b_i,b_k\)。\(n\le2\times10^5\)。

先特判掉数字种类不同的情况。然后有两个结论：\(1.\) 如果数组中存在相同元素则一定可以；\(2.\) 如果两数组逆序对数量奇偶性相同则答案为可以，否则不行。

可以发现操作四次就是选择 \((i,j,k,l)\)，交换 \(b_i,b_j\) 和 \(b_k,b_l\)。我们可以发现若存在两个元素相同，那么我们就可以通过四次操作交换任意两个位置的元素。并且当逆序对数量奇偶性相同则一定 Yes。

G - Polygon and Points

题意：给定凸多边形，多次询问一个点在多边形内部/外部/边上。\(n,m\le2\times10^5\)。

前置知识：一点点蒜几：如果 \(\vec{P}\times\vec{Q}>0\)，则 \(\vec{P}\) 在 \(\vec{Q}\) 的顺时针方向；如果 \(<0\)，则 \(\vec{P}\) 在 \(\vec{Q}\) 的逆时针方向；如果 \(=0\)，则 \(\vec{P}\) 与 \(\vec{Q}\) 同向或反向。

蒜几板子，但我不会蒜几。考虑把凸包分成几个三角形，类似这样：

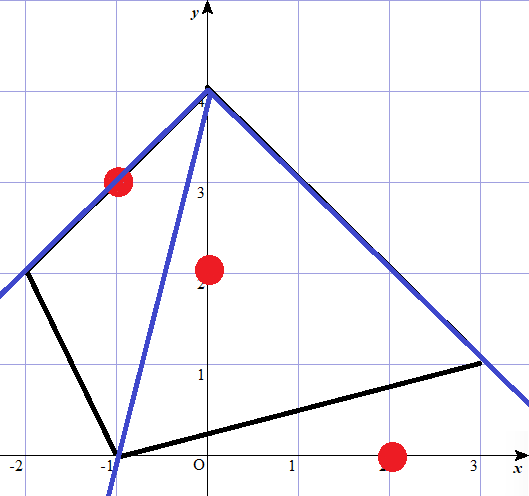
这样我们就可以二分找到点所在的三角形，然后判断点与线段的关系即可。注意特判点在 \(p_{0}p_{1},p_{0}p_{n-1}\) 上的情况。

AtCoder Beginner Contest 297

F - Minimum Bounding Box 2

题意：在一个初始全白的 n*m 矩阵中随机染黑 k 个点，定义一种染色方案的代价为能包住 k 个点的最小矩阵的面积，求期望代价。\(n,m\le1000\)。

假设最小矩阵不大于 \(a\times b\)，则共有 \(\binom{ab}{k}\) 种方案。但是这样会算重，需要容斥一下算出最小矩阵等于 \(a\times b\) 的方案。

G - Constrained Nim 2

题意：nim 游戏，但是每次取 [l,r] 个。\(n\le2\times10^5,a_i,l,r\le10^9\)。

赛时遇到这种东西一般我们打表找 SG 的规律。结论：\(SG(x)=\left\lfloor\frac{x\bmod(l+r)}{l}\right\rfloor\)。

证明：数学归纳法。\(x\in[0,l-1]\) 时必败，\(x\in[l,l+r-1]\) 时必胜。假设对于 \(x\in[k(l+r),k(l+r)+(l+r-1)]\) 时结论成立，则 \(x\in[(k+1)(l+r),(k+1)(l+r)+l-1]\) 只能从 \(x\in[k(l+r)+l,k(l+r)+(l+r-1)]\) 的必胜局面转移过来，必败；\(x\in[(k+1)(l+r)+l,(k+1)(l+r)+l+r-1]\) 只能从 \(x\in[(k+1)(l+r),(k+1)(l+r)+l-1]\) 的必败局面转移过来，必胜。

AtCoder Beginner Contest 298

G - Strawberry War

题意：把一个格子上有数的矩形分成 k+1 个小矩形，求最小的切割代价（一种切割方案的代价为每个小矩形上数字之和的极差）。\(n,m\le6\)。

枚举最小值，记忆化搜索最大值最小的方案数。

AtCoder Beginner Contest 299

D - Find by Query

题意：交互。长度为 n 的 01 串 s 满足 \(s_1=0,s_n=1\)。至多询问 20 次 \(s_i\) 的值，求一个 \(s_i\neq s_{i+1}\) 的位置，保证有解。\(n\le2\times10^5\)。

若 \(s_l=0,s_r=1\)，则在 [l,r] 中一定存在 \(s_i\neq s_{i+1}\) 的位置，二分即可。

E - Nearest Black Vertex

题意：给一张保证联通的无向图（边权为 1）每个点染黑/白色，满足 k 个形如“\(p_i\) 与最近的黑色点相距 \(d_i\)” 的限制，求一种染色方案。\(n,m,k\le2000\)。

对于到 \(p_i\) 距离小于 \(d_i\) 的点，他们必须染成白色；到 \(p_i\) 距离等于 \(d_i\) 的点，记录他们。最后把所有能染黑的都染黑即可。无解有两种情况：有到 \(p_i\) 距离小于 \(d_i\) 的点必须染成黑色、没有到 \(p_i\) 距离等 \(d_i\) 的点可以染成黑色。

F - Square Subsequence

题意：问有多少 T 满足 TT（两个 T 相连）是 S 的子序列。\(\left|S\right|\le100\) 且只包含小写字母。

定义 \(t_{i,c}\) 表示最小的满足 \(s_j=c,j\ge i\) 的 \(j\)。因为不能算重，钦定在所有合法的位置中只会选取最前面一个。举个例子：\(S=\color{black}\text{abbacbca},T=\color{black}\text{abc}\)，则我们只会看 \(\color{red}\text{ab}\color{black}\text{ba}\color{red}\text{c}\color{black}\text{bca}\) 而不会看类似 \(\color{red}\text{a}\color{black}\text{b}\color{red}\text{b}\color{black}\text{a}\color{red}\text{c}\color{black}\text{bca},\color{red}\text{a}\color{black}\text{b}\color{red}\text{b}\color{black}\text{acb}\color{red}\text{c}\color{black}\text{a}\) 这样的。枚举 \(q_0\) 表示第二个 T 的开头的位置，可以算出第一个 T 的开头的位置 \(p_0\)。\(f_{i,j}\) 表示第一/二个 T 结尾为 \(i/j\) 的个数，有转移 \(f_{i,j}=\sum f_{i',j'}\)，其中 \(i',j'\) 满足 \(t_{i',s_i}=i,t_{j',s_j}=j\)。上式可以优化成成我为人人的形式。时间 \(\text{O}(Ln^3)\)，其中 \(L\) 表示字符集大小。

G - Minimum Permutation

题意：在序列 a 中找到一个字典序最小的，且为 m 的排列的子序列。\(n,m\le2\times10^5\)。

直接贪。设还未在排列中出现过的数的集合为 S，则我们取的当前数的位置一定在 S 中每种数最后出现位置的最小值之前。

AtCoder Beginner Contest 300

摆了，没打。

E - Dice Product 3

题意：你有一个初始为 1 的变量 \(x\) 和一个六面骰子，你会重复以下流程直到 \(x\) 不小于 \(n\)：掷骰子，把上面的数乘到 \(x\) 上。求最终 \(x=n\) 的概率。答案对 \(998244353\) 取模，\(n\le10^{18}\)。

发现如果 \(n\) 含有除了 \(2,3,5\) 以外的质因子一定无解。然后如果你扔出 1，后面的情况也是一样的，可以把 1 删掉。dfs 即可。

F - More Holidays

题意：有一个长为 \(n\) 的只包含x和o的字符串 \(s\)，字符串 \(t\) 由 \(s\) 重复 \(m\) 次组成。现在你可以把 \(t\) 中恰好 \(k\) 个为x的位置改成o，最大化 \(t\) 中最长的连续o的长度。\(n\le3\times10^5\)，\(m\le10^9\)。保证 \(s\) 中至少有一个x，且 \(k\) 不大于 \(t\) 中x 的总数。

G - P-smooth number

题意：求不小于 n 的所有正整数中质因子大小不超过 p 的数有多少个。\(n\le10^{16},p\le100\)。

meet-in-the-middle。